电子学/节点分析
外观
< 电子学
电子学 | 前言 | 基础电子学 | 复杂电子学 | 电学 | 机器 | 电子学历史 | 附录 | 编辑
节点是电路中连接元器件的部分。根据基尔霍夫电流定律,进入节点的所有电流都必须离开节点。节点上的每个点都具有相同的电压,无论它与每个元器件的距离多么近,因为元器件之间的连接是完美的导体。这种电压称为节点电压,是节点与任意参考点(接地点)之间的电压差。接地点是一个定义为电压为零的节点。应仔细选择接地点以方便分析。请注意,接地点不一定表示与地面的实际连接,它只是一个使分析更简单的工具。例如,如果一个节点的电压为 5 伏,则该节点与接地点之间的电压降将为 5 伏。
请注意,在实际电路中,节点由导线构成,这些导线不是完美的导体,因此电压在节点上的每个位置都不完全相同。这种区别仅在要求苛刻的应用中很重要,例如低噪声音频、高速数字电路(如现代计算机)等。如果我们查看特定电路的功能,工程师可能能够选择彼此相对的检查点,这表示电流穿过另一个点的两个点,这可能是测试电路以确定节点工作原理的另一种方法。
节点分析是基于KCL方程的形式化程序。
步骤
- 识别所有节点。
- 选择一个参考节点。用参考(接地)符号识别它。一个好的选择是具有最多分支的节点,或者一个可以立即为您提供另一个节点电压的节点(例如,在电压源下方)。
- 为其他节点分配电压变量(这些是节点电压)。
- 为每个节点编写一个KCL方程(将离开节点的所有电流相加,并设置为零)。将这些方程重新排列成A*V1+B*V2=C的形式(或类似于具有更多电压变量的方程)。
- 求解步骤 4 中的方程组。可以使用多种技术:简单的代入法、克莱姆法则、伴随矩阵法等。
- 受控电流源
- 解决方案:为每个节点编写KVL方程。然后用节点电压表示额外变量(电流源所依赖的任何变量)。重新排列成上面步骤 4 中的形式。如步骤 5 中所示求解。
- 独立电压源
- 问题:我们不知道电压源的电流。我们无法为电压源连接到的节点编写KCL方程。
- 解决方案:如果电压源位于参考节点和任何其他节点之间,则我们已经获得了“免费”的节点电压:节点电压必须等于电压源值!否则,使用“超级节点”,包括源及其连接的节点。为进入和离开超级节点的所有电流编写KCL方程。现在我们有一个方程和两个未知数(节点电压)。另一个关联这些电压的方程是由电压源提供的方程(V2-V1=源值)。此新的方程组可以如上所述在步骤 5 中求解。
- 受控电压源
- 解决方案:与独立电压源相同,但多了一个步骤。首先编写超级节点KCL方程。然后用节点电压表示源控制量(依赖量?)。重新排列方程使其采用A*V1+B*V2=C的形式。如上所述求解方程组。
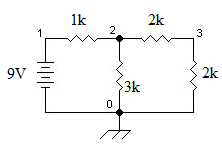
节点 0:(定义为接地点)
节点 1:(自由节点电压)
节点 2:
节点 3:
得到以下线性方程组:
因此,解决方案为:
另一种使用KCL的解决方案是根据节点2求解节点电压;