 NASA 兰利研究中心的超音速喷气发动机测试设施和测试,以评估噪声排放
NASA 兰利研究中心的超音速喷气发动机测试设施和测试,以评估噪声排放
预测气动噪声的一种直接方法是求解一般三维非定常可压缩数值模拟中的 Navier-Stokes 方程。不幸的是,除了在有限区域内非常简单的学术配置之外,这几乎是无法实现的。声学类比的想法是重新表述气体动力学的完整方程,从远处观察者的角度提供均匀运动中均匀介质中的等效波动方程。此条件导致通常线性声学问题[1] 的简化。最系统地使用的形式主义是利希特尔的类比以及 Curle 和 Ffowcs Williams & Hawkings 所做的扩展,因为它们提供了广泛的适用性。
必须明确说明的是,类比的目标不是本质上推导出精确的结果或数值系数,而是从与经典波动方程相关的标准程序中推断出一般规律。需要来自实验、CFD 或分析方法的关于主要流动特征的初步知识才能应用这些类比。此外,提取声学结果的流动变量的精度程度对于确保预测方法的相关性至关重要。
参考文献 [2] [3],下面的开发源于气动声学维基页面。
 ..........................质量守恒方程 (E1)
..........................质量守恒方程 (E1)
其中  和
和  分别表示流体的密度和速度,它们依赖于空间和时间,而
分别表示流体的密度和速度,它们依赖于空间和时间,而  是实质导数。
是实质导数。
接下来是动量守恒方程,它由下式给出
 ..........................动量守恒方程 (E2)
..........................动量守恒方程 (E2)
其中  是热力学压力,而
是热力学压力,而  是来自 Navier–Stokes 方程的柯西应力张量的粘性(或无迹)部分。
是来自 Navier–Stokes 方程的柯西应力张量的粘性(或无迹)部分。
步骤 1: 将 (E1) 乘以  并将其加到 (E2) 中,得到
并将其加到 (E2) 中,得到

步骤 2: 对 (E1) 关于时间求导,对 (E2) 求散度,并将后者从前者中减去,得到

步骤 3: 从最后一个方程的两边减去 ,其中
,其中 是介质在其平衡(或静止)状态下的声速,并重新整理,得到
是介质在其平衡(或静止)状态下的声速,并重新整理,得到
![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =\nabla \cdot \left[\nabla \cdot (\rho \mathbf {v} \otimes \mathbf {v} )-\nabla \cdot \sigma +\nabla p-c_{0}^{2}\nabla \rho \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471371077cd60e5c6ef74c2df8a482bfb7f3f688)
它等价于
![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =(\nabla \otimes \nabla ):\left[\rho \mathbf {v} \otimes \mathbf {v} -\sigma +(p-c_{0}^{2}\rho )\mathbb {I} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/612e7b49b9ae21a4ad4361a54229226eaeeb7fdc)
其中 是单位张量,而
是单位张量,而 表示(双重)张量收缩算子。
表示(双重)张量收缩算子。
使用 _爱因斯坦记号_,Lighthill 方程可以写成

其中  是所谓的 Lighthill 应力张量
是所谓的 Lighthill 应力张量  ,更多细节将在下一节提供。其中:
,更多细节将在下一节提供。其中: 是雷诺的惯性[check spelling] 应力张量
是雷诺的惯性[check spelling] 应力张量  是雷诺的粘性应力张量
是雷诺的粘性应力张量  代表所有由于熵非均匀性产生的影响(对于具有高温度梯度的高温射流很重要)
代表所有由于熵非均匀性产生的影响(对于具有高温度梯度的高温射流很重要)
航空声学工程师需要在近似值的第一个步骤中预测涡轮发动机产生的噪声,即传播介质中局部不稳定流。Lighthill (1952) 的基本思想是重新表述气体动力学的一般方程,以推导出波动方程。特征变量是密度波动,因为它在气体中的声波是由压缩性引起的。没有进行特殊的假设,也没有引入线性化。
 ...............................Lighthill 方程
...............................Lighthill 方程
其中 : 称为 Lighthill 张量
称为 Lighthill 张量
如果在等式两边加上相同的量,该方程仍然成立。加上 : ,其中
,其中  是未受扰动气体的特征声速(准确地说,是流场周围介质中的声速,在应用中;这与流场中的局部声速
是未受扰动气体的特征声速(准确地说,是流场周围介质中的声速,在应用中;这与流场中的局部声速  不同)。然后,在左侧形成波动算子,并将右侧的所有其他项移除,得到
不同)。然后,在左侧形成波动算子,并将右侧的所有其他项移除,得到
![{\displaystyle \ {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}{\frac {\partial ^{2}\rho }{\partial x_{j}^{2}}}={\frac {\partial ^{2}}{\partial x_{i}\partial x_{j}}}[\rho V_{i}V_{j}+(P-c_{0}^{2}\rho )\delta _{ij}-\tau _{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2ddb38c9610afcf63ea4e164ed29cc87681cb3b)
该结果是著名的 Lighthill 方程。当应用于声学的实际问题时,由于右边的所有项都可以忽略不计(根据与声波传播相关的合理假设,例如小振幅、等熵运动[4]),它简化为远离流动的均匀波动方程。Lighthill 方程的另一种形式可以用压力而不是密度来表示,如下所示
 .....................*关于压力波动的 LightHill 方程*
.....................*关于压力波动的 LightHill 方程*
也许这个不太常见,因为密度波动与可压缩效应直接相关,而压力波动可以存在以补偿流体中的惯性加速度。然而,当涉及温度不均匀性时,压力波动非常适合。
Lighthill 张量的每一项的解释
声学源可以分为三个不同的类别:
 单极声源
单极声源
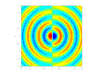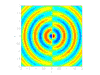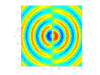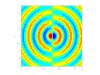
- 单极声源:
 球形声源或离散声源,提供随时间波动的流量
球形声源或离散声源,提供随时间波动的流量  。只有在遇到固体表面时才会出现。
。只有在遇到固体表面时才会出现。
 偶极声源
偶极声源
- 偶极声源:
 类似于两个并排放置的单极声源,它们具有相反的相位
类似于两个并排放置的单极声源,它们具有相反的相位  和
和  。偶极声源与力
。偶极声源与力  相关,根据我们结合的单极声源所创建的轴线。与单极声源一样,它们只有在域中涉及固体表面时才会出现。
相关,根据我们结合的单极声源所创建的轴线。与单极声源一样,它们只有在域中涉及固体表面时才会出现。
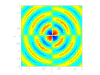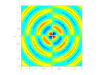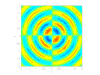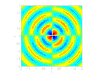 四极声源
四极声源
- 四极声源:
 由两个并排且相位相反的偶极声源构成,这些声源来自湍流涡旋,通常在低速流动中被忽略。它们起源于 Navier-Stokes 方程中的剪切项。
由两个并排且相位相反的偶极声源构成,这些声源来自湍流涡旋,通常在低速流动中被忽略。它们起源于 Navier-Stokes 方程中的剪切项。
作为气体动力学一般方程的推论,莱特希尔方程是精确的。所有气动声学过程,包括流动非均匀性产生的声音,声音在流动中的传播以及粘度或热传导引起的声能耗散,都被考虑在内。因此,由于等式右侧包含待确定的声场,并且不能被认为是真正的源项,所以该方程不能像使用线性声学的纯波方程那样易于处理。因此,我们需要独立于声学变量来近似这个项,这对应于忽略某些机制。为了消除这个基本困难,莱特希尔提出了一些简化,这些简化是基于这样的想法: **流体混合产生的声音是主要的机制**,特别是在航空学中感兴趣的高雷诺数情况下。这相当于优先考虑与流体惯性相关的机械效应,而将热力学效应视为次要效应。
莱特希尔方程是适定方程,因为它假设源位于流动内部,而不是流动外部。在传播区域,它简化为齐次波方程。但是,为了在源附近求解,必须使用现象比较进行近似。
莱特希尔的类比经常被用于计算喷气噪声,在这种类型的应用中,我们有导致简化的特定条件 [5]
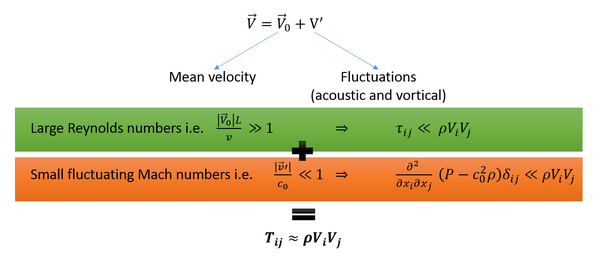
工业环境中使用的实际近似
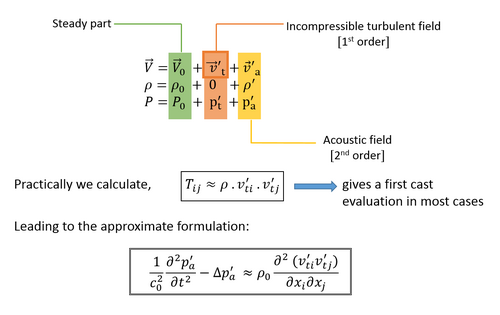
该近似使方程在某种意义上成为线性声学中波方程的显式方程,可以通过格林函数技术形式地求解。当使用数值方法来描述流动时,可以消除一些假设以进行更准确的评估,并将该方程用于后处理流动数据。
 伪声现象的描述及其对近场和远场假设以计算声压的影响
伪声现象的描述及其对近场和远场假设以计算声压的影响
如果熵非均匀性在扰动流中占主导地位,则源看起来像是等效的单极子
使用里布纳分离和不可压缩流体定律

得出最终的近似莱特希尔方程
 ..................... *近似莱特希尔方程*
..................... *近似莱特希尔方程*
1969年,弗劳克斯-威廉姆斯与霍金斯是第一批提出基本方程来预测流动中叶片产生的噪声的科学家 [6]。
(存在几种 FWH 类比的公式,这里有一个适用于叶片噪声描述现象的公式)
从莱特希尔方程推导出来,它表明旋转体中产生声学源的波动压力是特定非齐次波方程的解

其中,  是从源点到观察点的向量坐标,
是从源点到观察点的向量坐标,  是源域中的时间。
是源域中的时间。
源项  可以写成以下求和形式
可以写成以下求和形式

- 第一项
 代表由流体体积位移产生的 *厚度噪声*。风扇叶片具有厚度和体积。当转子旋转时,每个叶片的体积会置换流体体积,从而导致附近区域的压力波动,进而产生噪声。这种噪声在运行频率处是调频的,对于冷却风扇来说通常很弱,因为它们的转速相对较低。因此,风扇叶片的厚度几乎不影响电子冷却风扇的噪声。(这种噪声对于高速涡轮机械,例如直升机旋翼,可能变得很严重。)
代表由流体体积位移产生的 *厚度噪声*。风扇叶片具有厚度和体积。当转子旋转时,每个叶片的体积会置换流体体积,从而导致附近区域的压力波动,进而产生噪声。这种噪声在运行频率处是调频的,对于冷却风扇来说通常很弱,因为它们的转速相对较低。因此,风扇叶片的厚度几乎不影响电子冷却风扇的噪声。(这种噪声对于高速涡轮机械,例如直升机旋翼,可能变得很严重。)
- 第二项被称为 *负载噪声*,它来自于移动表面上力场
 的波动。在转子中,它起源于流体和叶片之间的非定常气动力。在计算模型中,该项由表面分布的偶极子表示。(对于风扇来说占主导地位)
的波动。在转子中,它起源于流体和叶片之间的非定常气动力。在计算模型中,该项由表面分布的偶极子表示。(对于风扇来说占主导地位)
- 最后一项是 *剪切噪声*,它由叶片表面上的四极子组成 [7]。
Ffowcs Williams & Hawkings 理论允许在知道格林函数中的源项的情况下求解此方程。
在所有四极子项显著且必须计算的应用中(优先发生在高速情况下),计算可能变得很繁琐,因为源分布在体积内部,其边界没有明确定义。相比之下,表面源项的计算要简单得多,并且边界清晰。如果 CFD 必须在围绕表面的有限域中使用,并且如果计算能够再现声学近场,则可以通过在非局部控制面(可以由用户定义)而不是物理表面上获取信息,提出一种更方便的解决声学问题的方法 [8]。可以应用双层势描述,在贝塞尔函数假设下求解亥姆霍兹方程。这种 Ffowcs Williams & Hawkings 类比的推广形式在最近的计算声气动力学 (CAA) 中被广泛使用。
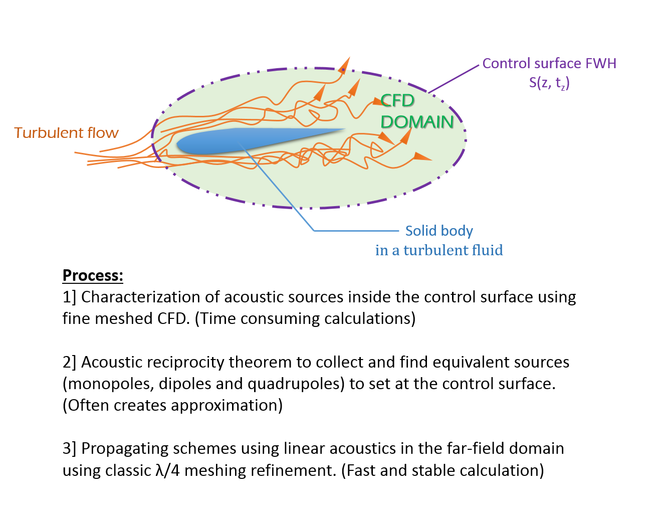 使用 FWH 类比和围绕气动外形的可渗透表面的声气动力学计算模拟
使用 FWH 类比和围绕气动外形的可渗透表面的声气动力学计算模拟
注意:控制面内的 CFD 域必须实现到生成的湍流系统完全发展为止(例如,使用 k- 准则)。
准则)。
类比的形式优势是将声气动力学问题表述为一个典型的线性声学问题,通过定义等效源,这些等效源将在均匀介质中产生与从流动和表面配置在观察者位置听到的相同声音。初始气体动力学方程的难度转移到源项的描述中。形式解是使用线性声学的理论基础推导出来的,但如果等效源项没有在其他地方确定,它可能毫无用处。使用 Lighthill 和 FWH 类比允许工程师例如以更低的计算时间成本计算飞机发动机的噪声。
美国宇航局和 CERFACS 机构正在进行密集的研究,试图开发更有效的计算方案,以提供改进的设计工具,让汽车工程师对噪声预测充满信心,并为下一代产品开发气动机械声学设计。
进行近似意味着丢弃预计可以忽略不计的现象,保留主要特征。这仅仅是在提出一种解释。
[1]Goldstein, M. E. (1976). 声气动力学。纽约,麦格劳 - 希尔国际图书公司,1976 年。305 页,1。
[2]Tam, C. K. (1995). 计算声气动力学 - 问题和方法。AIAA 杂志,33(10), 1788-1796。
[3]Wang, M., Freund, J. B., & Lele, S. K. (2006). 流动产生的声音的计算预测。流体力学年鉴,38, 483-512。
[4]Colonius, T., Lele, S. K., & Moin, P. (1993). 用于直接计算气动声学产生的边界条件。AIAA 杂志,31(9), 1574-1582。
[5] Williams, J. F. (1969). 流体动力噪声。流体力学年度回顾,1(1), 197-222。
[6] Williams, J. F., & Hawkings, D. L. (1969). 湍流和任意运动表面产生的声音。伦敦皇家学会哲学学报。A 系列,数学和物理科学,264(1151), 321-342。
[7] Ianniello, S. (1999). 通过 Ffowcs Williams-Hawkings 方程进行的四极子噪声预测。AIAA 杂志,37(9), 1048-1054。
[8]Di Francescantonio, P. (1997). 用于预测声音辐射的一种新的边界积分公式。声学与振动杂志,202(4), 491-509。


















![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =\nabla \cdot \left[\nabla \cdot (\rho \mathbf {v} \otimes \mathbf {v} )-\nabla \cdot \sigma +\nabla p-c_{0}^{2}\nabla \rho \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/471371077cd60e5c6ef74c2df8a482bfb7f3f688)
![{\displaystyle {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}\nabla ^{2}\rho =(\nabla \otimes \nabla ):\left[\rho \mathbf {v} \otimes \mathbf {v} -\sigma +(p-c_{0}^{2}\rho )\mathbb {I} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/612e7b49b9ae21a4ad4361a54229226eaeeb7fdc)













![{\displaystyle \ {\frac {\partial ^{2}\rho }{\partial t^{2}}}-c_{0}^{2}{\frac {\partial ^{2}\rho }{\partial x_{j}^{2}}}={\frac {\partial ^{2}}{\partial x_{i}\partial x_{j}}}[\rho V_{i}V_{j}+(P-c_{0}^{2}\rho )\delta _{ij}-\tau _{ij}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2ddb38c9610afcf63ea4e164ed29cc87681cb3b)



















