工程声学/冲击波的定性描述

冲击波的定义

在机械波传播的一般情况下，假设介质的强度性质可以用空间和时间的连续函数来描述。在压力振幅变得非常大的极限情况下，波传播会演变成波前变得不连续，必须用从波前未受扰动的热力学状态到波后最终热力学状态的跳跃来描述。

这种类型的传播扰动，它产生压力、温度、焓、内能、密度和粒子速度的不连续变化，被称为冲击波。冲击波在下图中示意性地表示

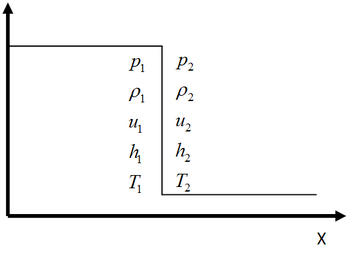
冲击波最终可以被解释为横向机械波，其脉冲波长不可定义，以远大于介质声速的传播速度不连续地改变介质的状态。

冲击波的形成和衰减

"冲击波"

考虑在弹性固体中冲击波是如何形成的最直观，因为这种行为原则上可以扩展到流体。对于线性弹性材料，压缩载荷下的行为可以大致分为两种情况。在弹性范围内，变形（应变）与施加在其上的应力成正比。超过某个临界应力水平（称为屈服应力），应变不再与应力成正比，材料开始表现出非线性行为——这就是塑性范围。

如果我们将材料中的声速定义为

$C^{2}={\frac {\partial P}{\partial \rho }}$

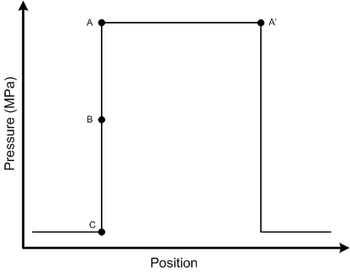
很明显，在弹性范围内，压力和密度呈线性关系，因此如果波的压力振幅低于材料的屈服应力，则传播速度是恒定的。然而，考虑一个振幅处于材料屈服强度以上压力的范围内的波，如下图所示

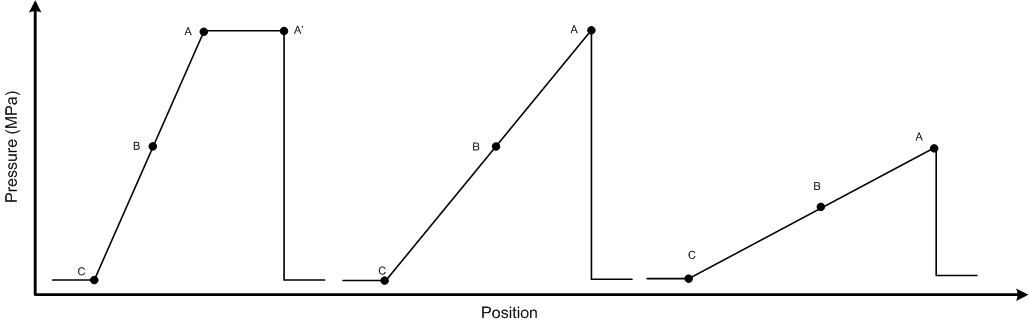
由于压力振幅超过了应力和应变之间线性比例关系的范围，因此波速不再恒定。通过查阅应力-应变曲线，可以明显看出波速随着超过弹性极限的压力的增加而增加。因此，波形的C点将具有最低的局部波速，而B点和A点将依次具有越来越高的波速。因此，波形中最高压力部分的传播速度快于低压部分，最终将追赶上它们。该过程的时间推移如下图所示

当平滑的波脉冲通过材料传播时，瞬时速度较快的波部分会追赶上速度较慢的部分，脉冲本身会变得越来越陡峭，直到它呈现出与冲击波相关的熟悉的、不连续的轮廓。因此，任何压力振幅大于材料屈服强度的波最终都会“冲击”并变得不连续，这是由于波速随压力的增加而呈非线性增加。

人们很容易认为，如果我们将冲击波的演化在时间上进一步回放，垂直线的顶部将继续超过底部，冲击波前沿将变得倾斜。实际上，由于存在一个竞争性的波过程，它起到衰减冲击的作用，因此这种情况不会发生。

冲击波稀疏

一旦冲击波在材料中形成，它就不能无限地传播，除非它是由活塞机械驱动或在爆轰波中通过耦合化学反应自支撑。将表明，冲击波的衰减和最终消散也是弹性极限以上压力、密度和波速之间非线性关系的自然结果。

考虑以下方形脉冲冲击波

检查点 A': 它正在以波速 $C_{0}$ 运动到未受冲击的材料中，相应的粒子速度为 $\nu _{0}$。相比之下，点 A 正在以更高得多的压力和密度运动到已经受冲击的材料中，因此具有更高的粒子速度，$\nu _{A'}$ 和波速 $C_{A'}$。因此，点 A 将比点 A' 运动得快得多，很快就会超过前沿。现在检查点 C。它已被缓解到环境条件，因此具有较低的相关波速。因此，它将逐渐落后于点 A。当冲击波传播时，线 A-C 将伸长并因此向下倾斜。这可以看作冲击脉冲幅度在越来越大的前沿厚度上的平均。这种平均作用会衰减脉冲，直到压力衰减到弹性极限以下，冲击波演变为声波。实际上，线 A-C 是一种波过程，其传播速度快于冲击波前沿。这种波被称为稀疏波，它是冲击波过程的基本特征。稀疏波衰减过程在下面的图中描述。

特征线法描述冲击波

虽然之前的讨论对于理解冲击波的行为非常直观，但所有这些结果都可以通过特征线法和黎曼不变量对非线性波动方程的数学求解直接获得。特征线法是一种通过将偏微分方程简化为常微分方程组来求解偏微分方程的技术，方法是对现有的坐标系进行参数化，将其转换为一个新的系统，在这个新系统中，偏微分方程的特性在新的系统中的曲线保持不变。在该方法中揭示的轮廓被称为特征线。

考虑一组基本的非线性弹性波动方程

$\ \epsilon ={\frac {\rho _{0}}{\rho }}$ 应变-密度关系

$\ \sigma =\sigma (\epsilon )$ 本构方程

$\ {\frac {\partial \rho }{\partial t}}+\nu {\frac {\partial \rho }{\partial x}}+\rho {\frac {\partial \nu }{\partial t}}=0$ 质量守恒

$\ \rho \left({\frac {\partial \nu }{\partial t}}+\nu {\frac {\partial \nu }{\partial x}}\right)={\frac {\partial \sigma }{\partial x}}$ 动量守恒

和特征坐标

$\ \xi =\xi (x,t)$

$\ \zeta =\zeta (x,t)$

受约束条件，其中 $\ x=x(X,t)$

$\ {\frac {\partial \zeta }{\partial t}}=C{\frac {\partial \zeta }{\partial X}}$

$\ {\frac {\partial \xi }{\partial t}}=-C{\frac {\partial \xi }{\partial X}}$

其中我们定义

$\ C=\left({\frac {1}{\rho _{0}}}{\frac {d\sigma }{d\epsilon }}\right)^{\frac {1}{2}}$

请注意，我们在这里实际上使用了波速作为压力和密度的函数的表达式！

得出约束方程

$\ {\frac {\partial \zeta }{\partial t}}=(C\epsilon -\nu ){\frac {\partial \zeta }{\partial x}}$

$\ {\frac {\partial \xi }{\partial t}}=-(C\epsilon +\nu ){\frac {\partial \xi }{\partial x}}$

将约束方程与微分 $d\zeta ={\frac {\partial \zeta }{\partial x}}dx+{\frac {\partial \zeta }{\partial t}}dt$ 和 $d\xi ={\frac {\partial \xi }{\partial x}}dx+{\frac {\partial \xi }{\partial t}}dt$ 结合得到 

$d\zeta ={\frac {\partial \zeta }{\partial x}}[dx-(\nu -C\epsilon )dt]$

$d\xi ={\frac {\partial \xi }{\partial x}}[dx-(\nu +C\epsilon )dt]$

然后这些方程得出新坐标系等高线的斜率

$\ {\frac {dx}{dt}}=\nu +C\epsilon$ 当 $\ d\xi =0$

$\ {\frac {dx}{dt}}=\nu -C\epsilon$ 当 $\ d\zeta =0$

现在，我们必须应用这些关系将波方程的表达式从 $\ (x,t)$ 空间转换为 $\ (\zeta ,\xi )$ 空间。对本构方程求时间导数，并代入特征线的斜率得到

$\ {\frac {\partial \sigma }{\partial x}}=-(C\epsilon )^{2}{\frac {\partial \rho }{\partial x}}$

$\ {\frac {\partial \sigma }{\partial t}}=-(C\epsilon )^{2}{\frac {\partial \rho }{\partial y}}$

为了简单起见，进行代换 $\ c=C\epsilon$

将代入质量守恒和动量守恒方程得到

$\ {\frac {\partial \sigma }{\partial t}}+\nu {\frac {\partial \sigma }{\partial x}}=\rho c^{2}{\frac {\partial \nu }{\partial x}}$

${\frac {\partial \nu }{\partial t}}+\nu {\frac {\partial \nu }{\partial x}}={\frac {1}{\rho }}{\frac {\partial \sigma }{\partial x}}$

这些可以组合起来，并通过偏导数链式法则展开求解得到

$\ {\frac {\partial \nu '}{\partial \zeta }}={\frac {1}{\rho c}}{\frac {\partial \sigma '}{\partial \zeta '}}$

$\ {\frac {\partial \nu '}{\partial \xi }}=-{\frac {1}{\rho c}}{\frac {\partial \sigma '}{\partial \xi '}}$

这些是在 $\zeta$ 和 $\xi$ 空间中的特征方程。

为了求解特征轮廓，我们必须从某个参考状态积分到某个最终状态，并参照不变量，因此

$\ J_{+}(\xi )=\nu -\nu ^{0}-\int _{1}^{\epsilon }{C(\epsilon )\,d\epsilon }$

$\ J_{-}(\zeta )=\nu -\nu ^{0}+\int _{1}^{\epsilon }{C(\epsilon )\,d\epsilon }$

这两个方程表示波系统的黎曼不变量。它们可以组合起来得到特征方程，其中应力和粒子速度的组合不发生变化，如下所示

$\ \nu -\nu ^{0}={\frac {1}{2}}(J_{+}(\xi )+J_{-}(\zeta ))$

$\ \int _{1}^{\epsilon }{C(\epsilon )\,d\epsilon }={\frac {1}{2}}(-J_{+}(\xi )+J_{-}(\zeta ))$

简单波解

简单波是特征空间中波方程的解，其中一个不变量是常数。考虑一个非线性波，我们设置

$\ J_{-}(\zeta )=0$

这使得应力、应变、粒子速度和声速仅成为$\xi$的函数。从之前推导出的坐标轮廓的斜率，我们得到

$\ {\frac {dX}{dt}}=\nu (\xi ^{i})+c(\xi ^{i})$

直接积分这些轮廓得到 

$\ \xi =t-{\frac {x}{\nu (\xi )+c(\xi )}}$

因此，特征空间中非线性方程的简单波解可以描述为将一个指定的横向运动脉冲转换为一组具有不同斜率的直线特征。每条线都可以解释为脉冲上一个特定点的 x-t 历史。

如果我们计算黎曼积分

$\ \nu -\nu ^{0}={\frac {1}{2}}J_{+}\left[t-{\frac {x}{\nu +c}}\right]$

$\ \int _{1}^{\epsilon }{C(\epsilon )\,d\epsilon }=-{\frac {1}{2}}J_{+}\left[t-{\frac {x}{\nu +c}}\right]$

我们得到重要的结果

$\ {\frac {d(v+c)}{d\epsilon }}\leq 0$

这个不等式从数学上证实了我们之前关于波速在非线性（塑性）状态下随压力增加而增加的论述，并阐明了一个重要概念：波速等于粒子速度和声速之和。

特征空间中的简单波解之间的关系可以通过以下概念与激波的形成联系起来：具有不同斜率的特征最终会在某个时刻相交。

激波源于波

从数学上可以证明，非线性波轮廓的交点是一个数学上的间断，从而验证了我们关于激波是状态间断的概念。

为了简便起见，考虑一个相对于位置是粒子速度斜坡的波 - 这类似于我们第一节中之前的定性示例，但用粒子速度绘制而不是压力（两者是相关的）。描述这个斜坡的方程是

$\ \nu =-mx$

应用我们对简单波特征的解，我们得到

$\ \nu =m[(\nu +c)t-x]$

为了使此解易于处理，我们必须使用状态方程来数学地联系波速和粒子速度。由于我们没有指定所讨论的材料，因此可以简单地假设这种关系是线性的，因此

$\ c=\lambda u+c_{0}$

将此代入我们得到的关于速度的关系，得到

$\nu ={\frac {m(c_{0}t-x)}{1-\lambda mt}}$

显然，当 $t={\frac {1}{\lambda m}}$ 时，粒子速度的值是未定义的，简单波解失效，我们形成了激波。但是，当 $m$ 为负数时，$\nu$ 的值永远不会趋于无穷大，我们有一个膨胀波。如果我们在 x-t 图上绘制斜坡底部的一个点（对应于我们之前讨论中的点 C）和斜坡顶部的另一个点（对应于点 A）的位置历史，我们可以直观地了解这些特征是如何变化的。

重要的是要注意，我们的数学和概念讨论最终产生了关于激波形成和行为的类似描述。在数学讨论中，我们可以看到每个特征对应于 $(P,x)$ 或 $(P,t)$ 空间中描绘的波形的特定点的轨迹。这些特征的历史记录了波形特定部分是如何超越或滞后于其他部分的。对于一组收敛的特征，交点对应于数学奇点和激波的形成。对于发散的特征，我们可以看到波形点开始在空间中扩散 - 这明显类似于膨胀波的描述。

强激波和弱激波

在特征方法的背景下，激波是由特征线的收敛产生的任何间断。根据激波如何影响热力学状态轨迹，激波解分为两种类型。弱激波定义为最终状态和参考状态之间的变化几乎与等效的简单特征收敛波相同的情况。在这种情况下，导致状态变化的过程是等熵的，材料从参考状态加载到最终状态的路径由等熵线描述。

相反，强激波是所有可能状态轨迹不与等熵线重合，而是遵循不同加载路径的间断解。

关于状态轨迹的讨论将在引入 Hugoniot 后变得更加清晰。

参考文献

1. 非线性流体和固体中波传播导论；D.S. Drumheller；1998
2. 炸药工程；Paul W. Cooper；1996
3. 激波和爆炸；P.L. Sachdev；2004