工程声学/平面波的反射、透射和折射

二维平面波

二维平面压力波可以用笛卡尔坐标系描述，将波数分解为 x 和 y 分量，

$\mathbf {p} (x,y,t)=\mathbf {P} e^{j(\omega t-K_{x}x-K_{y}y)}.$

代入一般的波动方程得到

$\nabla ^{2}\mathbf {p} -{\frac {1}{c_{o}^{2}}}{\frac {\partial ^{2}\mathbf {p} }{\partial t^{2}}}=0,$

$\mathbf {P} (-K_{x}^{2}-K_{y}^{2})+{\frac {\omega ^{2}}{c_{o}^{2}}}\mathbf {P} =0,$

$K={\frac {\omega }{c_{o}}}={\sqrt {K_{x}^{2}+K_{y}^{2}}}.$

波数变成一个矢量量，可以用方向余弦表示，

${\vec {K}}=K_{x}{\boldsymbol {\hat {\imath }}}+K_{y}{\boldsymbol {\hat {\jmath }}}=K\cos(\alpha ){\boldsymbol {\hat {\imath }}}+K\cos(\beta ){\boldsymbol {\hat {\jmath }}}.$

斜入射平面波

考虑介质 1 中的斜入射平面波，它以 $\theta _{i}$ 角相对于法线入射到边界。部分波以 $\theta _{r}$ 角反射回介质 1，其余部分以 $\theta _{t}$ 角透射到介质 2。

$\mathbf {p_{1}} =\mathbf {P_{i}} e^{j(\omega t-\cos \theta _{i}K_{1}x-\sin \theta _{i}K_{1}y)}+\mathbf {P_{r}} e^{j(\omega t+\cos \theta _{r}K_{1}x-\sin \theta _{r}K_{1}y)}$

$\mathbf {p_{2}} =\mathbf {P_{t}} e^{j(\omega t-\cos \theta _{t}K_{2}x-\sin \theta _{t}K_{2}y)}$

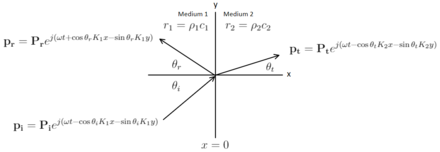斜入射平面波的反射和透射。

注意，波的频率在边界处不会改变，但特定声阻抗从介质 1 改变到介质 2。传播速度在每种介质中不同，因此波数在边界处发生变化。需要满足两个边界条件。

1. 声压在边界处必须连续。
2. 垂直于边界的粒子速度分量在边界处必须连续。

施加第一个边界条件得到

$\mathbf {p_{1}} (x=0)=\mathbf {p_{2}} (x=0),$

$\mathbf {P_{i}} e^{-j\sin \theta _{i}K_{1}y}+\mathbf {P_{r}} e^{-j\sin \theta _{r}K_{1}y}=\mathbf {P_{t}} e^{-j\sin \theta _{t}K_{2}y}.$

为了使连续性成立，指数必须全部相等

$K_{1}\sin \theta _{i}=K_{1}\sin \theta _{r}=K_{2}\sin \theta _{t}.$

这有两个含义。首先，入射波的角度等于反射波的角度，

$\sin \theta _{i}=\sin \theta _{r}$

其次，斯涅尔定律被恢复，

${\frac {\sin \theta _{i}}{c_{1}}}={\frac {\sin \theta _{t}}{c_{2}}}.$

第一个边界条件可以用声压反射和透射系数来表示

$1+\mathbf {R} =\mathbf {T} .$

施加第二个边界条件得到

$\mathbf {u_{1x}} (x=0)=\mathbf {u_{2x}} (x=0),$

$\mathbf {u_{i}} \cos \theta _{i}+\mathbf {u_{r}} \cos \theta _{r}=\mathbf {u_{t}} \cos \theta _{t}.$

利用声阻抗的定义，可得

${\frac {\mathbf {P_{i}} }{r_{1}}}\cos \theta _{i}-{\frac {\mathbf {P_{r}} }{r_{1}}}\cos \theta _{r}={\frac {\mathbf {P_{t}} }{r_{2}}}\cos \theta _{t}.$

利用反射系数、透射系数和声阻抗比，可以得到

$1-\mathbf {R} ={\frac {\cos \theta _{t}}{\cos \theta _{i}}}{\frac {\mathbf {T} }{\zeta }}.$

求解压力反射系数，可以得到

$\mathbf {R} =\mathbf {T} -1={\frac {{\frac {\cos \theta _{i}}{\cos \theta _{t}}}\zeta -1}{{\frac {\cos \theta _{i}}{\cos \theta _{t}}}\zeta +1}}={\frac {{\frac {r_{2}}{\cos \theta _{t}}}-{\frac {r_{1}}{\cos \theta _{i}}}}{{\frac {r_{2}}{\cos \theta _{t}}}+{\frac {r_{1}}{\cos \theta _{i}}}}}.$

求解压力透射系数，可以得到

$\mathbf {T} =\mathbf {R} +1={\frac {2{\frac {\cos \theta _{i}}{\cos \theta _{t}}}\zeta }{{\frac {\cos \theta _{i}}{\cos \theta _{t}}}\zeta +1}}={\frac {2{\frac {r_{2}}{\cos \theta _{t}}}}{{\frac {r_{2}}{\cos \theta _{t}}}+{\frac {r_{1}}{\cos \theta _{i}}}}}.$

求解声阻抗比，可以得到

$\zeta ={\frac {\cos \theta _{t}}{\cos \theta _{i}}}{\Big (}{\frac {1+\mathbf {R} }{1-\mathbf {R} }}{\Big )}={\frac {\cos \theta _{t}}{\cos \theta _{i}}}{\Big (}{\frac {\mathbf {T} }{2-\mathbf {T} }}{\Big )}.$

瑞利反射系数

瑞利反射系数将斯涅尔定律中的入射角与 $\mathbf {R}$、$\mathbf {T}$ 和 $\zeta$ 的方程式中的透射角联系起来。从三角恒等式，

$\cos ^{2}\theta _{t}+\sin ^{2}\theta _{t}=1$

并使用斯涅尔定律，

$\cos \theta _{t}={\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}.$

注意，为了使透射角为实数，

$c_{2}<{\frac {c_{1}}{\sin \theta _{i}}}$

必须满足。因此，存在一个临界入射角，使得

$\sin {\theta _{c}}={\frac {c_{1}}{c_{2}}}.$

瑞利反射系数代回 $\mathbf {R}$、$\mathbf {T}$ 和 $\zeta$ 的方程式，以获得仅用阻抗和入射角表示的表达式。

$\mathbf {R} =={\frac {\cos \theta _{i}\zeta -{\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}}{\cos \theta _{i}\zeta +{\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}}}$

$\mathbf {T} ={\frac {2\cos \theta _{i}\zeta }{\cos \theta _{i}\zeta +{\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}}}$

$\zeta ={\frac {\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}{\cos \theta _{i}}}{\Big (}{\frac {1+\mathbf {R} }{1-\mathbf {R} }}{\Big )}={\frac {\sqrt {1-{\Big (}{\frac {c_{2}}{c_{1}}}\sin \theta _{i}{\Big )}^{2}}}{\cos \theta _{i}}}{\Big (}{\frac {\mathbf {T} }{2-\mathbf {T} }}{\Big )}.$