工程声学/圆形管道中具有顺应性壁的声传播

在具有顺应性壁的管道中，声传播的应用很多。这些应用范围从液压应用（例如水锤）到生物力学应用（例如动脉中的压力脉冲）。在研究圆形管道中的声传播时，管道壁通常被认为是刚性的，因此流体中的任何压力扰动都不会影响管道壁。然而，如果假设管道壁是顺应性的，即在遇到压力扰动时，管道壁可以变形，那么这将改变声传播的速度。在现实中，如果流体中的压力扰动（它是流体密度的函数）非常小，以至于管道壁的变形可以忽略不计，那么刚性壁假设将是有效的。但是，如果假设管道壁很薄，即半径的 1/20 或更小，或者如果管道壁由杨氏模量和密度较低的塑料材料制成，或者如果所含流体是“重”的，那么刚性壁近似将不再成立。在这种情况下，假设管道壁是顺应性的。

在 Morse & Ingard [1] 的书中，壁刚度定义为 K_w，它是压力扰动 p 与由 p 引起的管道横截面积分数变化的比率。当然，这种压力扰动 p 不是静止的，必须考虑壁的惯性。由于壁的变形是由流体中的压力扰动引起的，因此这是一个典型的流体-结构相互作用问题，其中流体中的压力扰动会导致结构变形，而结构变形反过来又会修改压力扰动。

与声音在具有刚性壁的管道中传播不同，在刚性壁管道中，声压沿管道轴向传播；一部分压力用于径向拉伸管道。显然，由于包含了管道壁的位移，这变成了一个流体-结构相互作用问题。

分析

在本分析中，预计传播速度将取决于管道壁的材料特性，即杨氏模量和密度。此外，随着分析的展开，很明显传播速度将随激发频率而变化，这与刚性壁管道中的波传播不同。请记住，这里介绍的分析非常简单。当然，根据流体和结构模型的不同，可以得到更准确的结果。在本分析中，目标是提供对具有顺应性壁的圆形管道中声传播的基本物理理解。

假设

1. 一维分析
2. 所有粘性和热耗散都被忽略
3. 分析是按单位长度进行的
4. 不考虑平均流速

流体

这里将考虑两个简化的流体方程

$-{\frac {\partial u}{\partial x}}=\kappa {\frac {\partial p}{\partial t}}\dots \dots .Eq(1)$

和

$-{\frac {\partial p}{\partial x}}={\rho }_{f}{\frac {\partial u}{\partial t}}\dots \dots .Eq(2)$

其中 $\kappa ={\frac {1}{{\rho }_{f}c^{2}}}$，$u$ 是流体质点速度，$p$ 是流体压力。

第一个方程是连续性方程，其中密度项通过应用理想气体定律 $p=\rho RT$ 和等熵气体定律 $c^{2}=\gamma RT$ 被替换为压力项。

由于顺应性壁的存在，流体经历了额外的压缩性效应，根据 Morse & Ingard [1]，这种额外的压缩性是根据壁刚度 (K) 推导出来的。壁刚度定义为压力与横截面积分数变化的比率。通过将 K 引入方程 1，得到

$-{\frac {\partial u}{\partial x}}=\left(\kappa +{\frac {1}{K}}\right){\frac {\partial p}{\partial t}}\dots \dots Eq\left(3\right)$

如果考虑管道的质量，则必须包含额外的质量参数 M_w。

然后，壁的总刚度阻抗为

$Z_{w}=j\omega M_{w}+{\frac {K_{w}}{j\omega }}=j{\frac {M_{w}}{\omega }}\left({\omega }^{2}-{\omega }_{n}^{2}\right)$

将该墙壁阻抗视为一个顺应性项（即 $K=j\omega Z_{w}$），代入方程式 3 得

$-{\frac {\partial u}{\partial x}}=\left(\kappa +{\frac {1}{M_{w}({{\omega }_{n}^{2}-\omega }^{2})}}\right){\frac {\partial p}{\partial t}}$

这里，${\omega }_{n}={\sqrt {\frac {K_{w}}{M_{w}}}}$.

此外，通过提取 ${\kappa }$，该表达式变为

$-{\frac {\partial u}{\partial x}}=\kappa \left({\frac {M_{w}\left({{\omega }_{n}^{2}-\omega }^{2}\right)+{\rho }_{f}c^{2}}{M_{w}({{\omega }_{n}^{2}-\omega }^{2})}}\right){\frac {\partial p}{\partial t}}$

经过一些操作，它得到

$-{\frac {\partial u}{\partial x}}=\kappa \left({\frac {{{\omega }_{1}^{2}-\omega }^{2}}{{{\omega }_{n}^{2}-\omega }^{2}}}\right){\frac {\partial p}{\partial t}}$

其中 ${\omega }_{1}^{2}={\omega }_{n}^{2}+{\frac {{\rho }_{f}c^{2}}{M_{w}}}$

对于刚性壁，当 $K_{w}\to \infty$，${\omega }_{n}^{2}\to \infty$，${\omega }_{1}^{2}\to \infty$，因此，$-{\frac {\partial u}{\partial x}}=\kappa {\frac {\partial p}{\partial t}}$，这将回到方程式 1。

如果使用阻抗类比，即压力是电压，速度是电流，那么

$C=\ \kappa \left({\frac {{{\omega }_{1}^{2}-\omega }^{2}}{{{\omega }_{n}^{2}-\omega }^{2}}}\right)$ ，其中 C 是每单位长度的壁顺性。

声速由 ${\sqrt {\frac {1}{LC}}}$ 决定，因此

$c_{p}=c{\sqrt {\left({\frac {{{\omega }_{n}^{2}-\omega }^{2}}{{{\omega }_{1}^{2}-\omega }^{2}}}\right)}}$

这里，$c_{p}$ 是相速度，它取决于激励频率，${\omega }$，声波是色散的。当激励频率低于固有频率，${\omega }_{n}$ 时，相速度低于流体中自由波速度。

下一步是识别 K_w 和 M_w，这将通过结构响应确定。

结构

假设未变形管道的直径为 D，变形后变为 $D+\triangle D$。在这种情况下，面积变化为 ${\frac {\pi }{4}}\left(2D\triangle D+{\left(\triangle D\right)}^{2}\right)$。两者之间的比率为 ${\frac {\triangle A}{A}}={\frac {2\triangle D}{D}}+{\left({\frac {\triangle D}{D}}\right)}^{2}$。因此，壁刚度为

$K_{w}={\frac {\triangle pD}{2\triangle D}}$.

其中，该值的倒数被称为柔度或 可扩张性（一个生物医学术语）。

为了确定项 ${\frac {\triangle D}{D}}$，有必要利用牛顿定律和胡克定律来观察结构响应。

考虑一个直径为 D、厚度为 h、张力为 T 的半管横截面，

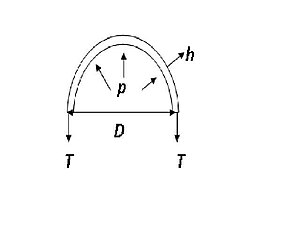
圆柱形管道的环向应力由下式给出，

$\sigma =p{\frac {D}{2h}}$。应用胡克定律，可以确定应变 $\varepsilon$，通过

$\varepsilon ={\frac {\sigma }{E}}$.

进行一些替换后，

$\varepsilon ={\frac {pD}{2hE}}$

对于小应变，

$\Delta \varepsilon ={\frac {\Delta pD}{2hE}}={\frac {\Delta D}{D}}$。因此，

$K_{w}=E{\frac {h}{D}}$

这就是壁刚度，它仅仅是管道弹性特性的函数。

如果考虑管道每单位长度的质量，则

$M_{w}={\rho }_{s}\pi h(D+h)$.

最后，可以绘制相速度和壁阻抗与激励频率的关系图。

讨论

在模拟中，厚度与直径之比，${\frac {h}{D}}$ 为 0.1，材料为钢，其$\rho =7800{\frac {kg}{m^{3}}}$ 和 $E=2x10^{11}Pa$。假设内部填充的流体为空气，其$\rho =1.21{\frac {kg}{m^{3}}}$，自由波速为 $c=343{\frac {m}{s}}$。

文件：Tws1.jpg

在此图中，“o”表示相速度的实部，“+”表示相速度的虚部。直线表示空气中的声速，数值为 $c=343{\frac {m}{s}}$。在此图中，波的传播只有在相速度为实数时才有可能。有两个重要的频率值得我们密切关注。第一个是空结构的固有频率，即 ${\omega }_{n}$，以及流体负载结构的固有频率，${\omega }_{1}$。在此图中，${\omega }_{n}=450Hz$，而${\omega }_{1}=550Hz$。

与刚性管道中的一维波传播不同，在刚性管道中传播速度是恒定的，相速度取决于激励频率。结果表明，随着激励频率接近 ${\omega }_{n}$，传播速度会降低。在 ${\omega }_{n}$ 和 ${\omega }_{1}$ 之间，相速度为虚数，这意味着这两个频率之间没有波可以传播。一旦频率超过 ${\omega }_{1}$，相速度大于 343 m/s 的自由波速。随着激励频率的增加，相速度接近自由波速。

当激励频率增加时，部分流体能量被用来激励管子，直到激励频率与 ${\omega }_{n}$ 相匹配。超过 ${\omega }_{n}$，由于这两个频率之间，没有真正的波传播。

对于一个非常坚硬的管子，例如 $E=2x10^{20}Pa$，相速度正好等于空气中的自由波速，这是一个常数。这与之前讨论的在一维刚性管道中的波传播一致。

文件:Tws2.jpg

当刚度降低到钢的 1/100 时，与钢管相比，存在许多差异。首先，在低频下，相速度较慢。这是因为较低的壁刚度，壁更容易拉伸，因此可以吸收更多能量。此外，该系统具有更低的 ${\omega }_{n}$ 和 ${\omega }_{1}$。

文件:Tws3.jpg

从以上分析，可以得出以下结论：

1. 管子的刚度、壁厚和密度会显着影响相速度。

2. 刚度的降低会降低低频的传播速度。波在更低的频率下也变得衰减。这是因为自然频率降低了。随着刚度的增加，传播速度接近自由波速，无论频率范围如何。这就是刚性壁的情况。

3. 具有柔性壁的管道中的波传播速度是色散的，因为它很大程度上取决于频率。相速度与刚性壁中的相速度有很大差异。

4. 非传播区称为阻带。这里，可以修改壁的特性来创建更大的阻带。因此，具有柔性壁的管道可以被视为一种带通滤波器。

参考文献

[1]. Morse & Ingard (1968), "Theoretical Acoustics", Princeton University Press, Princeton, New Jersey