工程声学/Rankine-Hugoniot 跳跃方程

守恒方程和推导

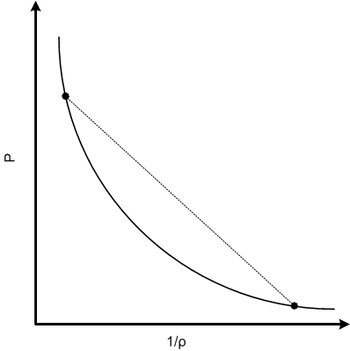
为了进行工程计算，需要将冲击前后的状态联系起来的方程。将状态联系起来的两个最基本的表达式之一是 $(P,\rho )$ Hugoniot 方程，它将压力和密度关联起来，

$\ P=f(\rho )$

此表达式可以通过简化规范守恒方程来推导出

质量守恒

$\rho _{1}\nu _{1}=\rho _{o}\nu _{o}\,$

动量守恒

$p_{1}+\rho _{1}\nu _{1}^{2}=p_{o}+\rho _{o}\nu _{o}^{2}$

能量守恒

$e_{1}+{\frac {p_{1}}{\rho _{1}}}+{\frac {1}{2}}\nu _{1}^{2}=e_{o}+{\frac {p_{o}}{\rho _{o}}}+{\frac {1}{2}}\nu _{o}^{2}$

完全求解跳跃条件所需的冲击参数有压力、粒子速度、比内能、密度和冲击速度。有 4 个状态变量，只有 3 个方程，因此需要一个额外的方程来关联一些状态，使问题易于处理。这个方程被称为状态方程 (EOS) - 存在许多 EOS 用于各种应用。最常见的 EOS 是理想气体定律，它可以用来将方程组简化为稳态流体中具有恒定比热的 Hugoniot 表达式。

${\frac {p_{1}}{p_{2}}}={\frac {(\gamma +1)-(\gamma -1){\frac {\rho _{2}}{\rho _{1}}}}{(\gamma +1){\frac {\rho _{2}}{\rho _{1}}}-(\gamma -1)}}$

对于一般的非线性弹性材料，不存在可以从第一原理推导出的状态方程。然而，大量的实验数据表明，几乎所有材料都显示出粒子速度和冲击速度之间存在线性关系（特征线方法示例中线性假设的准确性现在更加明确了！）。

$\ U=C_{o}+s\nu$

此方程也称为 $U-\nu$ 平面上的冲击 Hugoniot 方程。

将这种线性关系与动量和质量方程结合起来，可以得出几乎所有固体材料的 $P-\rho$ 平面上的 Hugoniot 表达式。

$\ P=C_{o}^{2}{\frac {{\frac {1}{\rho _{0}}}-{\frac {1}{\rho }}}{\left({\frac {1}{\rho _{0}}}-{\frac {s}{\rho }}\right)^{2}}}$

路径和跃变条件

Hugoniot 描述了材料在冲击波后方可能存在的所有热力学状态的轨迹，这些轨迹投影到二维状态-状态平面上。因此，它是一组平衡状态，并不专门代表材料发生转变的路径。

再次考虑我们对强冲击和弱冲击的讨论。据称弱冲击是等熵的，并且等熵代表了材料通过具有会聚特性的等效波（称为压缩波）从初始状态加载到最终状态的路径。在弱冲击的情况下，Hugoniot 因此将直接落在等熵线上，并且可以直接用作等效路径。

在强冲击的情况下，我们不能再直接进行这种简化，但是对于工程计算而言，等熵线足够接近 Hugoniot，因此可以做出相同的假设。

如果 Hugoniot 近似于“等效”压缩波状态之间的加载路径，则冲击加载路径的跃变条件可以通过在初始状态和最终状态之间画一条直线来确定。这条线称为瑞利线，方程如下

$\ P_{1}-P_{0}=U^{2}\left(\rho _{0}-{\frac {\rho _{0}^{2}}{\rho _{1}}}\right)$