材料弹性概述/示例问题

示例 1

问题陈述

给定弹性体上的一点，其应力状态为 ${\textstyle {\boldsymbol {\sigma }}}$，确定主应力以及原始方向与最大剪切应力方向之间的角度。使用解析方程和莫尔圆作图两种方法解决此问题。应力单位为兆帕。

${\boldsymbol {\sigma }}={\begin{pmatrix}72&21&0\\21&32&0\\0&0&0\end{pmatrix}}$

解决方案

我们将使用两种方法来解决这个问题。首先使用解析解，然后使用莫尔圆。

解析解

我们有以下方程

${\begin{aligned}\sigma '_{11}={\frac {\sigma _{11}+\sigma _{22}}{2}}+{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)+\sigma _{12}sin\left(2\theta \right)\\\sigma '_{22}={\frac {\sigma _{11}+\sigma _{22}}{2}}-{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)-\sigma _{12}sin\left(2\theta \right)\end{aligned}}$

以及

${\begin{aligned}\sigma '_{12}={\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)+\sigma _{12}cos\left(2\theta \right)\end{aligned}}$

其中，主应力是在旋转后的参考系中。当 $\sigma '_{12}=0$ 时，系统处于主方向，并且 $\sigma '_{11}=\sigma _{p1}$ 和 $\sigma '_{22}=\sigma _{p2}$。设置 $\sigma '_{12}=0$ 并求解得到

$tan\left(2\theta \right)={\frac {2\sigma _{12}}{\sigma _{22}-\sigma _{11}}}$

代入本问题中给定的应力，我们得到 $\theta =23.2$°。代入 $\theta$ 的值和给定的 ${\boldsymbol {\sigma }}$ 值，得到 $\sigma '_{11}=\sigma _{p1}=81$ MPa，$\sigma '_{22}=\sigma _{p2}=23$ MPa，以及 $\sigma '_{12}=0$ MPa，这验证了它确实是主轴。

如果给定一个处于主方向的应力状态，那么在我们上面的旋转参考系中，${\boldsymbol {\sigma '}}$ 的 $\sigma _{12}$ 项为零。通过对 $\sigma '_{12}$ 求导，并将其设为零，然后求解 $\theta$，即可找到最大剪切方向。

${\frac {d\sigma '_{12}}{d\theta }}={\frac {d}{d\theta }}\left({\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)\right)=\left(\sigma _{22}-\sigma _{11}\right)cos\left(2\theta \right)$

当 $\theta =45$° 时，达到最大值。这意味着最大值或最小值出现在 $23.2+45=68.2$°。将此值代入我们的方程以及 ${\boldsymbol {\sigma }}$ 可以得到 $\sigma '_{11}=\sigma _{p1}=52$ MPa，$\sigma '_{22}=\sigma _{p2}=52$ MPa 以及 $\sigma '_{12}=-29$ MPa，最小值。由于系统的对称性，再旋转 $90$° 会得到最大值，$\sigma '_{11}=\sigma _{p1}=52$ MPa，$\sigma '_{22}=\sigma _{p2}=52$ MPa 以及 $\sigma '_{12}=29$ MPa。

莫尔圆解法

展示此示例问题的莫尔圆表示的图。

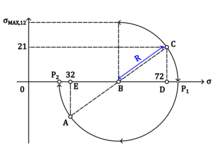
按照这里给出的图，

$Radius=AB=BC={\sqrt {BD^{2}+CD^{2}}}$

以及

$tan\left(2\theta \right)={\frac {CD}{BD}}$

假设 $CD=21$，$OD=72$ 和 $OE=32$， 我们得出结论：$AD=40$ 和 $EB=BD=20$。 因此，$Radius=29$ 和 $\theta =23.2$°。从主方向 $P1=OB+Radius=OE+EB+Radius=81$ MPa 和 $P2=P1-2Radius=23$ MPa。最小和最大剪切应力为 $\pm Radius=\pm 29$ MPa，可以通过将系统旋转 $23.2+45=68.2$° 和 $23.2+45+90=158.2=-21.8^{\circ }$ 找到。

示例 2

问题陈述

假设弹性体上某一点的应力状态为 ${\textstyle {\boldsymbol {\sigma }}}$，求主应力。应力单位为 MPa。[提示：只有一种绘制莫尔圆的方法。利用这一点简化你的工作。你会发现，一旦你画出图形，几乎不需要任何数学计算。]

${\boldsymbol {\sigma }}={\begin{pmatrix}0&6&8\\6&0&10\\8&10&0\end{pmatrix}}$

示例 3

问题陈述

给定一个弹性体上具有应力状态 ${\textstyle {\boldsymbol {\sigma }}}$ 的一点，并且绕 ${\textstyle x_{3}}$ 旋转产生应力状态 ${\textstyle {\boldsymbol {\sigma '}}}$，完全确定两种应力状态和未知参数 ${\textstyle q}$。应力以 MPa 为单位。

${\boldsymbol {\sigma }}={\begin{pmatrix}25q&\sigma _{12}&0\\\sigma _{21}&5q&0\\0&0&0\end{pmatrix}}~{\boldsymbol {\sigma '}}={\begin{pmatrix}50&5&0\\5&\sigma '_{22}&0\\0&0&0\end{pmatrix}}$

解决方案

图示了此示例问题的莫尔圆表示。阴影区域是相似三角形。

我们有以下方程

${\begin{aligned}\sigma '_{11}={\frac {\sigma _{11}+\sigma _{22}}{2}}+{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)+\sigma _{12}sin\left(2\theta \right)\\\sigma '_{22}={\frac {\sigma _{11}+\sigma _{22}}{2}}-{\frac {\sigma _{11}-\sigma _{22}}{2}}cos\left(2\theta \right)-\sigma _{12}sin\left(2\theta \right)\end{aligned}}$

以及

${\begin{aligned}\sigma '_{12}={\frac {\sigma _{22}-\sigma _{11}}{2}}sin\left(2\theta \right)+\sigma _{12}cos\left(2\theta \right)\end{aligned}}$

其中主应力在旋转后的参考系中。

这立即允许我们用 $\sigma '_{12}$ 和 $\theta$ 代替，以求得 $q=-1/2$。这给出 $\sigma _{11}=-12.5$ MPa 和 $\sigma _{22}=-2.5$。不变量关系

$\sigma _{11}+\sigma _{22}+\sigma _{33}=I_{1}$

允许

$\sigma _{11}+\sigma _{22}+\sigma _{33}=\sigma '_{11}+\sigma '_{22}+\sigma '_{33}$

通过代入，确定 $\sigma '_{22}=-65$ MPa。此时，除了 $\sigma _{12}$ 之外，所有参数都已确定。只需将其代入 $\sigma '_{11}$ 或 $\sigma '_{22}$ 就能求得 $\sigma _{12}=57.5$ MPa。最终的应力张量，以 MPa 为单位，为

${\boldsymbol {\sigma }}={\begin{pmatrix}-12.5&57.5&0\\57.5&-2.5&0\\0&0&0\end{pmatrix}}~{\boldsymbol {\sigma '}}={\begin{pmatrix}50&5&0\\5&-65&0\\0&0&0\end{pmatrix}}$

该解的莫尔圆表示如图所示。请注意，阴影三角形是相似的，因此如果以图形方式寻求解决方案，可以使用它们来简化解决方案。

示例 4

问题陈述

给定弹性体上一点，其应力状态为 ${\textstyle {\boldsymbol {\sigma }}}$，确定主应力以及原始方向与最大剪切应力方向之间的夹角。应力单位为 MPa。

${\boldsymbol {\sigma }}={\begin{pmatrix}18&12&9\\12&12&-6\\9&-6&6\end{pmatrix}}$

示例 5

问题陈述

用数学和文字解释对向量 ${\textstyle {\boldsymbol {a}}}$ 应用变换张量 ${\textstyle {\boldsymbol {T_{1}}}}$, ${\textstyle {\boldsymbol {T_{2}}}}$,${\textstyle {\boldsymbol {T_{3}}}}$, 和 ${\textstyle {\boldsymbol {T_{4}}}}$ 的影响。将相同的变换应用于二阶张量 ${\textstyle {\boldsymbol {Z}}}$。

${\boldsymbol {T_{1}}}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}~{\boldsymbol {T_{2}}}={\begin{pmatrix}-1&0&0\\0&-1&0\\0&0&-1\end{pmatrix}}~{\boldsymbol {T_{3}}}={\begin{pmatrix}-1&0&0\\0&1&0\\0&0&-1\end{pmatrix}}~{\boldsymbol {T_{4}}}={\begin{pmatrix}cos\left(\theta \right)&0&sin\left(\theta \right)\\0&1&0\\-sin\left(\theta \right)&0&cos\left(\theta \right)\end{pmatrix}}$

${\boldsymbol {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}~{\boldsymbol {Z}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}$

解决方案

回顾张量乘法的定义和爱因斯坦符号中使用的隐式求和，我们知道二阶张量 ${\boldsymbol {T}}$ 作用于向量 ${\boldsymbol {a}}$ 必然会产生类似于以下形式的项：

$a'_{2}=a_{1}T_{11}+a_{2}T_{12}+a_{3}T_{13}$

这类似于你之前见过的“普通”矩阵乘法。相反，将二阶变换张量作用于二阶张量 ${\boldsymbol {Z}}$ 需要进行双重求和，这会导致产生类似于以下形式的项：

$Z'_{12}=T_{11}T_{21}Z_{11}+T_{11}T_{22}Z_{12}+T_{11}T_{23}Z_{13}+T_{12}T_{21}Z_{21}+T_{12}T_{22}Z_{22}+T_{12}T_{23}Z_{23}+T_{13}T_{21}Z_{31}+T_{13}T_{22}Z_{32}+T_{13}T_{23}Z_{33}$

在处理这种包含 9 个项的求和式时，通常建议使用软件包来简化工作。结果如下所示。

变换张量 1 导致

${\boldsymbol {a'}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}$

这对应于恒等变换，即不修改张量。

变换张量 2 导致

${\boldsymbol {a'}}={\begin{pmatrix}-a_{1}\\-a_{2}\\-a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&Z_{12}&Z_{13}\\Z_{21}&Z_{22}&Z_{23}\\Z_{31}&Z_{32}&Z_{33}\end{pmatrix}}$

这种变换是反转变换。这可以从向量的行为中看出。有趣的是，它使 ${\boldsymbol {Z}}$ 不变。

变换张量 3 导致

${\boldsymbol {a'}}={\begin{pmatrix}-a_{1}\\a_{2}\\-a_{3}\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}&-Z_{12}&Z_{13}\\-Z_{21}&Z_{22}&-Z_{23}\\Z_{31}&-Z_{32}&Z_{33}\end{pmatrix}}$

此变换涉及跨越 $x_{1}$ 和 $x_{3}$ 方向的镜像。这等效于绕 $x_{2}$ 轴旋转 $180$°。

变换张量 4 导致 $${\boldsymbol {a'}}={\begin{pmatrix}a_{1}cos\left(\theta \right)+a_{3}sin\left(\theta \right)\\a_{2}\\a3cos\left(\theta \right)-a_{1}sin\left(\theta \right)\end{pmatrix}}~{\boldsymbol {Z'}}={\begin{pmatrix}Z_{11}cos\left(\theta \right)^{2}+Z_{13}cos\left(\theta \right)sin\left(\theta \right)+Z_{31}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}sin\left(\theta \right)^{2}&Z_{12}cos\left(\theta \right)+Z_{32}sin\left(\theta \right)&Z_{13}cos\left(\theta \right)^{2}-Z_{11}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}cos\left(\theta \right)sin\left(\theta \right)-Z_{31}sin\left(\theta \right)^{2}\\Z_{21}cos\left(\theta \right)+Z_{23}sin\left(\theta \right)&Z_{22}&Z_{23}cos\left(\theta \right)-Z_{21}sin\left(\theta \right)\\Z_{31}cos\left(\theta \right)^{2}-Z_{11}cos\left(\theta \right)sin\left(\theta \right)+Z_{33}cos\left(\theta \right)sin\left(\theta \right)-Z_{13}sin\left(\theta \right)^{2}&Z_{32}cos\left(\theta \right)-Z_{12}sin\left(\theta \right)&Z_{33}cos\left(\theta \right)^{2}-Z_{13}cos\left(\theta \right)sin\left(\theta \right)-Z_{31}cos\left(\theta \right)sin\left(\theta \right)+Z_{11}sin\left(\theta \right)^{2}\end{pmatrix}}$$ 该变换涉及绕 $x_{2}$ 轴旋转。将 $180$° 代入 $\theta$° 会得到与变换张量 3 相同的结果。

示例 6

问题陈述

考虑应力状态 ${\textstyle {\boldsymbol {\sigma }}}$。写一个将参考系旋转到主方向的变换张量。应力以 MPa 为单位给出。

${\boldsymbol {\sigma }}={\begin{pmatrix}72&21&0\\21&32&0\\0&0&0\end{pmatrix}}$

解决方案

我们从例子 1 中知道，解决方案是绕 $\theta =23.2$ 旋转 $x_{3}$ 轴，我们也知道旋转变换矩阵的形式（来自例子 5），所以解决方案是：

${\boldsymbol {\sigma }}={\begin{pmatrix}cos\left(\theta \right)&sin\left(\theta \right)&0\\sin\left(\theta \right)&cos\left(\theta \right)&0\\0&0&0\end{pmatrix}}$

其中 $\theta =23.2$.

例子 7

问题陈述

给定位移张量 ${\textstyle {\boldsymbol {e}}}$，确定旋转张量和应变张量。

${\boldsymbol {e}}={\begin{pmatrix}0.001&0.001&0.002\\-0.001&0.002&0.002\\0.001&0.003&0.002\end{pmatrix}}$

解决方案

我们可以将任何张量分解成一个完全对称张量和一个完全反对称张量，从而得到一个反对称旋转张量

${\boldsymbol {\omega }}={\begin{pmatrix}0&{\frac {e_{12}-e_{21}}{2}}&{\frac {e_{13}-e_{31}}{2}}\\{\frac {e_{21}-e_{12}}{2}}&0&{\frac {e_{23}-e_{32}}{2}}\\{\frac {e_{31}-e_{13}}{2}}&{\frac {e_{32}-e_{23}}{2}}&0\end{pmatrix}}={\begin{pmatrix}0&0.001&0.0005\\-0.001&0&-0.0005\\-0.0005&0.0005&0\end{pmatrix}}$

以及对称应变张量

${\boldsymbol {\varepsilon }}={\begin{pmatrix}e_{11}&{\frac {e_{12}+e_{21}}{2}}&{\frac {e_{13}+e_{31}}{2}}\\{\frac {e_{21}+e_{12}}{2}}&e_{22}&{\frac {e_{23}+e_{32}}{2}}\\{\frac {e_{31}+e_{13}}{2}}&{\frac {e_{32}+e_{23}}{2}}&e_{33}\end{pmatrix}}={\begin{pmatrix}0.001&0&0.0015\\0&0&0.0025\\0.0015&0.0025&0\end{pmatrix}}$

最终导致 ${\boldsymbol {e}}={\boldsymbol {\omega }}+{\boldsymbol {\varepsilon }}$.

示例 8

问题陈述

在线性、均匀、各向同性弹性理论中，对于给定的应力状态（单位为 MPa），已知泊松比为 0.40，剪切模量为 50 GPa，求解应变状态。确定静水应力、偏应力、应变膨胀和应变偏量。

${\boldsymbol {\sigma }}={\begin{pmatrix}10&2&2\\2&5&-3\\2&-3&-5\end{pmatrix}}$

解决方案

已知应力，因此求解需要确定应变，可以通过以下公式计算：

$\varepsilon _{ij}={\frac {1+\nu }{E}}\sigma _{ij}-{\frac {\nu }{E}}\sigma _{kk}\delta _{ij}$

已知泊松比 $\nu$ 和剪切模量 $G$，但要使用该公式，我们需要弹性模量 $E$。可以通过以下公式求解：

$G={\frac {E}{2\left(1-\nu \right)}}$

可以转化为：

$E=2G\left(1-\nu \right)$

代入后得出 $E=60$ GPa。最终的应变张量为：

${\boldsymbol {\varepsilon }}={\begin{pmatrix}{\frac {1+\nu }{E}}\sigma _{11}-{\frac {\nu }{E}}\left(\sigma _{22}+\sigma _{33}\right)&{\frac {\sigma _{12}}{2G}}&{\frac {\sigma _{13}}{2G}}\\{\frac {\sigma _{21}}{2G}}&{\frac {1+\nu }{E}}\sigma _{22}-{\frac {\nu }{E}}\left(\sigma _{11}+\sigma _{33}\right)&{\frac {\sigma _{23}}{2G}}\\{\frac {\sigma _{31}}{2G}}&{\frac {\sigma _{32}}{2G}}&{\frac {1+\nu }{E}}\sigma _{33}-{\frac {\nu }{E}}\left(\sigma _{11}+\sigma _{22}\right)\end{pmatrix}}={\begin{pmatrix}0.1667&0.0467&0.0467\\0.0467&0.0500&-0.0700\\0.0467&-0.0700&-0.1833\end{pmatrix}}.$

静水压力为

$\sigma _{m}={\frac {\sigma _{kk}}{3}}={\frac {\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}}={\frac {10+5-5}{3}}=3.33{\text{ GPa}}$

应变膨胀为

$\Delta =\left(1+\varepsilon _{11}\right)\left(1+\varepsilon _{22}\right)\left(1+\varepsilon _{33}\right)-1=\left(1+0.1667\right)\left(1+0.0500\right)\left(1+0.1833\right)-1=0.4496$

导致平均应变为

$\varepsilon _{m}={\frac {\Delta }{3}}={\frac {0.4496}{3}}=0.1499$

(请注意，当应变较小时 $\Delta \approx \varepsilon _{11}+\varepsilon _{22}+\varepsilon _{33}=0.400$，这将得到 $\varepsilon _{m}\approx 0.1333$。不幸的是，在这个例子中，应变相对较大。) 然后，通过从各自的张量对角线上减去平均应力和应变来确定偏应力和应变。

${\boldsymbol {\sigma '}}={\begin{pmatrix}10-3.33&2&2\\2&5-3.33&-3\\2&-3&-5-3.33\end{pmatrix}}={\begin{pmatrix}6.67&2&2\\2&1.67&-3\\2&-3&-8.33\end{pmatrix}}$

以及

${\boldsymbol {\varepsilon '}}={\begin{pmatrix}0.1667-0.1499&0.0467&0.0467\\0.0467&0.0500-0.1499&-0.0700\\0.0467&-0.0700&-0.1833-0.1499\end{pmatrix}}={\begin{pmatrix}0.0168&0.0467&0.0467\\0.0467&0.0999&-0.0700\\0.0467&-0.0700&-0.3332\end{pmatrix}}$

示例 9

问题陈述

在线性、均匀、各向同性弹性理论中，对于给定的应变状态，确定给定体积模量为 100 GPa 和 Lamé 参数为 50 GPa 时的应力状态。确定静水应力、偏应力、应变膨胀和应变偏量。

${\boldsymbol {\varepsilon }}={\begin{pmatrix}0.002&0.002&0.001\\0.002&0.002&0.001\\0.001&0.001&-0.001\end{pmatrix}}$

解决方案

我们已知应变，因此要得出解需要确定应力，应力可以通过以下公式确定：

$\sigma _{ij}={\frac {E}{1+\nu }}\varepsilon _{ij}-{\frac {\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}}\varepsilon _{kk}\delta _{ij}$

其中 ${\frac {\nu E}{\left(1+\nu \right)\left(1-2\nu \right)}}$ 是 Lamé 参数 $\lambda$。由于

$G={\frac {E}{2\left(1+\nu \right)}}$

以及

$G={\frac {3\left(K-\lambda \right)}{2}}$

我们知道

${\frac {E}{\left(1+\nu \right)}}=3\left(K-\lambda \right)$

应力表达式变为

$\sigma _{ij}=3\left(K-\lambda \right)\varepsilon _{ij}+\lambda \varepsilon _{kk}\delta _{ij}$

代入并求解得出

${\boldsymbol {\sigma }}={\begin{pmatrix}0.45&0.3&0.15\\0.3&0.45&0.15\\0.15&0.15&0.0\end{pmatrix}}$ GPa

静水压力为

$\sigma _{m}={\frac {\sigma _{kk}}{3}}={\frac {\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}}={\frac {0.45+0.45+0.0}{3}}=0.30{\text{ GPa}}$

应变膨胀为

$\Delta =\left(1+\varepsilon _{11}\right)\left(1+\varepsilon _{22}\right)\left(1+\varepsilon _{33}\right)-1=\left(1+0.002\right)\left(1+0.002\right)\left(1-0.001\right)-1=0.003$

导致平均应变为

$\varepsilon _{m}={\frac {\Delta }{3}}={\frac {0.003}{3}}=0.001$

一个有趣的观察是，应变膨胀和静水（平均）应力与体积模量相关 $\sigma _{m}=K\Delta$，在本例中为 $0.3=100\times 0.003$。在进行计算时，使用诸如此类的已知检查点来验证您的工作非常重要。

然后通过从各自的张量对角线中减去平均应力和应变来确定偏应力和应变。

${\boldsymbol {\sigma '}}={\begin{pmatrix}0.45-0.30&0.30&0.15\\0.30&0.45-0.30&0.15\\0.15&0.15&0.00-0.30\end{pmatrix}}={\begin{pmatrix}0.15&0.30&0.15\\0.30&0.15&0.15\\0.15&0.15&-0.30\end{pmatrix}}$

以及

${\boldsymbol {\varepsilon '}}={\begin{pmatrix}0.002-0.001&0.002&0.001\\0.002&0.002-0.001&0.001\\0.001&0.001&-0.001-0.001\end{pmatrix}}={\begin{pmatrix}0.001&0.002&0.001\\0.002&0.001&0.001\\0.001&0.001&-0.002\end{pmatrix}}$

示例 10

问题陈述

对于立方氧化锆单晶，其弹性常数约为 $c_{11}=575$, $c_{12}=115$ 和 $c_{44}=75$ GPa，确定在 $\left[100\right]$ 方向施加 0.001 的单轴应变所需的弹性能量。确定在 $\left[110\right]$ 方向施加 0.001 的单轴应变所需的弹性能量。计算齐纳各向异性比。使用各向同性弹性理论，弹性模量为 200 GPa，泊松比为 0.3，计算施加 0.001 的单轴应变所需的弹性能量。

解决方案

假设 $\left[100\right]$ 方向为 $x_{1}$ 方向。弹性能量，$U_{o}$，是

$U_{o}={\frac {1}{2}}\sigma _{ij}\varepsilon _{ij}$

所以

$dU_{o}={\frac {1}{2}}\sigma _{ij}d\varepsilon _{ij}$

在各向异性弹性理论的情况下

$\sigma _{ij}=c_{ijkl}\varepsilon _{kl}.$

在这种情况下，所有 $\varepsilon _{ij}=0$ 都为零，除了 $\varepsilon _{11}=0.001$。因此，所有 $\sigma _{ij}=0$ 都为零，除了 $\sigma _{11}=c_{1111}\varepsilon _{11}$，$\sigma _{22}=c_{1122}\varepsilon _{22}$ 和 $\sigma _{33}=c_{1122}\varepsilon _{33}$。

代入上述方程式：

${\begin{aligned}dU_{0}&=\varepsilon _{11}c_{1111}d\varepsilon _{11}+\underbrace {\varepsilon _{11}c_{1122}\ d\varepsilon _{22}+\varepsilon _{11}c_{1122}\ d\varepsilon _{33}} _{=\ 0\ upon\ integration}\\&=\varepsilon _{11}c_{1111}d\varepsilon _{11}\\\\U_{0}&=\int _{0}^{\varepsilon _{11}\ =\ 0.001}\varepsilon _{11}c_{11}d\varepsilon _{11}\\&=\left.c_{11}{\varepsilon _{11}^{2} \over 2}\ \right|_{0}^{0.001}\\&=(575*10^{9}\ Pa){0.001^{2} \over 2}\\&=288\ kJ\end{aligned}}$

例 11

问题陈述

对于一个立方氧化锆的单晶体，其弹性常数约为 $c_{11}=575$，$c_{12}=115$ 和 $c_{44}=75$ GPa，确定在 $\left[100\right]$ 方向施加 0.001 的单轴应变，然后在 $\left(001\right)$ 面上沿 $\left[010\right]$ 方向施加 0.001 的剪切应变所需的弹性能量。

解决方案

按照给定的操作顺序，首先我们在 $[100]$ 方向施加了 $0.001$ 的单轴载荷。（也在示例 10 中介绍）

请注意，我们的通用方程是 ${\textstyle dU=\sigma _{ij}\ d\varepsilon _{ij}}$ 和 ${\textstyle \sigma _{ij}=c_{ijkl}\varepsilon _{kl}}$。

重新说明应变张量：

$\varepsilon =\left({\begin{matrix}\varepsilon _{11}&0&0\\0&0&0\\0&0&0\end{matrix}}\right)$

由此我们得到非零的应力张量：

$\sigma =\left({\begin{matrix}\varepsilon _{11}c_{11}&0&0\\0&\varepsilon _{11}c_{12}&0\\0&0&\varepsilon _{11}c_{12}\end{matrix}}\right)$

因此，唯一非零的 $d\varepsilon _{ij}$ 是 $d\varepsilon _{11}$，通过对 ${\textstyle dU}$ 的方程进行积分，我们得到：$U_{1}=288\ kJ$

现在让我们在 $(100)$ 面上沿 $[010]$ 方向施加剪切力 $0.001$。

我们新的应力张量是：

$\sigma =\left({\begin{matrix}\varepsilon _{11}c_{11}&\varepsilon _{12}c_{44}&0\\\varepsilon _{12}c_{44}&\varepsilon _{11}c_{12}&0\\0&0&\varepsilon _{11}c_{12}\end{matrix}}\right)$

这里，唯一非零的项是 $d\varepsilon _{12}$ 和 $d\varepsilon _{21}$。由于对称性，这两个项是等效的，因此我们可以求解其中一个，并将答案乘以二。

再次利用我们的基本能量方程，我们得到：

${\begin{aligned}dU&=\sigma _{ij}\ d\varepsilon _{ij}=\varepsilon _{12}c_{44}\ d\varepsilon _{12}\\\\U_{2}&=2\int _{0}^{\varepsilon _{12}}\varepsilon _{12}c_{44}\ d\varepsilon _{12}\\&=2\left[c_{44}{\varepsilon _{12}^{2} \over 2}\right]_{0}^{\varepsilon _{12}}\\&=(75*10^{9}\ Pa)0.001^{2}\\U_{2}&=75\ kJ\end{aligned}}$

最后，将 $U_{1}$ 和 $U_{2}$ 加起来，得到这种组合变换的总能量，我们最终得到 $363\ kJ$ 的答案。

示例 12

问题陈述

对于一个立方氧化锆的多晶体样品，其弹性常数约为 $c_{11}=575$, $c_{12}=115$, 和 $c_{44}=75$ GPa，使用各向同性弹性理论和 $200\ GPa$ 的弹性模量和 $0.3$ 的泊松比来计算施加应变状态的弹性能。

${\boldsymbol {\varepsilon }}={\begin{pmatrix}0.001&0.001&0.000\\0.001&0.000&0.000\\0.000&0.000&0.000\end{pmatrix}}$

如果多晶体材料的孔隙率约为 2%，这将对弹性模量产生多少影响？对于这种施加的应变，这将对弹性能产生多少影响？

解决方案

请注意，我们的通用方程是 ${\textstyle dU=\sigma _{ij}\ d\varepsilon _{ij}}$ 和 ${\textstyle \sigma _{ij}=c_{ijkl}\varepsilon _{kl}}$。

在这里，我们可以用弹性模量和泊松比来表示应力：

$\sigma _{ij}={E \over 1+\nu }\varepsilon _{ij}+{\nu E \over (1+\nu )(1-2\nu )}\varepsilon _{kk}\partial _{ij}$

其中后面的常数等价于拉梅常数 ($\lambda$)： $\lambda ={\nu E \over (1+\nu )(1-2\nu )}$

简要求解拉梅常数得到：

${\begin{aligned}\lambda &={\nu E \over (1+\nu )(1-2\nu )}\\&={0.3*200\ GPa \over (1+0.3)(1-2(0.3))}=115.3846\ GPa\end{aligned}}$

请记住，由于对称性 $\varepsilon _{12}$ 等于 $\varepsilon _{21}$，这个问题的非零应力是：

$\sigma =\left({\begin{matrix}{E \over 1+\nu }\varepsilon _{11}+\lambda \varepsilon _{11}&{E \over 1+\nu }\varepsilon _{12}&0\\{E \over 1+\nu }\varepsilon _{12}&\lambda \varepsilon _{11}&0\\0&0&\lambda \varepsilon _{11}\end{matrix}}\right)$

因此，我们可以将非零能量项写成：

${\begin{aligned}dU&=\sigma _{ij}\ d\varepsilon _{ij}\\&=\left({E \over 1+\nu }+\lambda \right)\varepsilon _{11}\operatorname {d} \!\varepsilon _{11}+\left({E \over 1+\nu }+\lambda \right)\varepsilon _{12}\operatorname {d} \!\varepsilon _{12}+\left({E \over 1+\nu }+\lambda \right)\varepsilon _{21}\operatorname {d} \!\varepsilon _{21}+\lambda \varepsilon _{11}\operatorname {d} \varepsilon _{11}+\lambda \varepsilon _{11}\operatorname {d} \varepsilon _{11}\\&=\left({E \over 1+\nu }+\lambda \right)\varepsilon _{11}\operatorname {d} \!\varepsilon _{11}+2\left({E \over 1+\nu }+\lambda \right)\varepsilon _{12}\operatorname {d} \!\varepsilon _{12}\\\\U&=\left.\left({E \over 1+\nu }+\lambda \right){1 \over 2}\varepsilon _{11}^{2}\right|_{0}^{\varepsilon _{11}}+\left.\left({E \over 1+\nu }\right)\varepsilon _{12}^{2}\right|_{0}^{\varepsilon _{12}}\\&=288\ kJ\end{aligned}}$