专家系统/模糊逻辑

专家系统

一位维基教科书用户提名此页面进行清理，因为

最近从维基百科导入，需要格式化

您可以帮助改进它。请查看任何相关讨论。

一位维基教科书用户提名此页面进行清理，因为

最近从维基百科导入，需要格式化

您可以帮助改进它。请查看任何相关讨论。

此页面的原始文本改编自维基百科。

关于模糊逻辑

维基百科在模糊逻辑中有相关信息

模糊逻辑源于模糊集理论，处理的是近似推理，而不是从经典谓词逻辑中精确推导出来的。可以把它看作是模糊集理论的应用方面，处理的是针对复杂问题经过深思熟虑的现实世界专家值（Klir 1997）。

真值程度经常与概率混淆。然而，它们在概念上是不同的；模糊真值代表的是对模糊定义的集合的隶属关系，而不是对某些事件或条件的可能性。例如，如果一个 100 毫升的玻璃杯中装有 30 毫升的水，那么对于两个模糊集 Empty 和 Full，人们可能会定义这个玻璃杯为 0.7 空和 0.3 满。请注意，空的概念是主观的，因此将取决于观察者或设计者。另一个设计者也可能同样设计一个集合隶属函数，其中玻璃杯在所有低于 50 毫升的值时都被认为是满的。概率设置首先定义玻璃杯的满度的标量变量，其次，定义条件分布，描述在给定特定满度级别的情况下，有人称玻璃杯为满的概率。请注意，条件化可以通过随机选择玻璃杯标签的特定观察者、确定性观察者的分布或两者来实现。虽然模糊逻辑在这种情况中避免谈论随机性，但这种简化同时掩盖了“玻璃杯是 0.3 满”这句话的真正含义。

模糊逻辑允许集合隶属值在（包含）0 到 1 之间，并且在它的语言形式中，允许像“稍微”、“相当”和“非常”这样的不精确概念。具体来说，它允许部分属于一个集合。它与模糊集和可能性理论有关。它由洛特菲·扎德于 1965 年在加州大学伯克利分校提出。

模糊逻辑在某些圈子里存在争议，并且被一些控制工程师和大多数认为概率是描述不确定性的唯一严格数学方法的统计学家所拒绝。批评者还认为，它不能是普通集合论的超集，因为隶属函数是根据常规集合定义的。

应用

模糊逻辑可用于控制家用电器，例如洗衣机（它会感知负载大小和洗涤剂浓度并相应地调整洗涤循环）和冰箱。

一个基本的应用可能是描述连续变量的子范围。例如，用于防抱死制动系统的温度测量可能具有几个独立的隶属函数，定义了控制制动器正常工作所需的特定温度范围。每个函数都将相同的温度值映射到 0 到 1 范围内的真值。这些真值可以用来确定如何控制制动器。

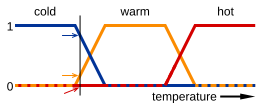
在这张图片中，冷、温和热是将温度刻度映射到函数的函数。刻度上的一个点具有三个“真值”——每个函数一个。对于用垂直线说明的特定温度，三个真值可以解释为描述温度，例如，“相当冷”（蓝色箭头），“略微温”（黄色箭头）和“不热”（红色箭头）。

误解和争议

模糊逻辑与“不精确逻辑”相同。: 模糊逻辑并不比任何其他形式的逻辑不精确：它是一种处理固有不精确概念的有组织的数学方法。“寒冷”的概念无法用方程来表达，因为虽然温度是一个量，但“寒冷”不是。然而，人们对“冷”有一定的概念，并且一致认为，在“冷”和“不冷”之间没有明确的界限，在那里某物在 N 度时是“冷的”，但在 N+1 度时是“不冷的”——由于二值原理，经典逻辑难以处理这个概念。结果没有确定的答案，因此被认为是一个“模糊”的答案。

模糊逻辑是表达概率的一种新方法。: 模糊逻辑和概率是表达不确定性的两种不同方法。虽然模糊逻辑和概率论都可以用来表示主观信念，但模糊集理论使用的是模糊集隶属的概念（即变量在多大程度上属于一个集合），概率论使用的是主观概率的概念（即我认为变量有多大可能属于一个集合）。虽然这种区别主要是哲学上的，但模糊逻辑导出的可能性度量与概率度量本身存在差异，因此它们不直接等效。然而，许多统计学家被布鲁诺·德·菲内蒂的工作所说服，认为只需要一种数学不确定性，因此模糊逻辑是不必要的。另一方面，巴特·科斯科认为概率是模糊逻辑的子理论，因为概率只处理一种不确定性。他还声称已经证明了从模糊子集概念推导出贝叶斯定理的推导过程。模糊逻辑的创造者洛特菲·扎德认为，模糊逻辑与概率在性质上是不同的，并不是概率的替代品。他创造了一个模糊的概率替代品，他称之为可能性理论。其他有争议的不确定性方法包括Dempster-Shafer 理论和粗糙集。

模糊逻辑将难以扩展到更大的问题。: 这种批评主要是由于条件可能性（模糊集理论中与条件概率等效的概念）存在问题（参见 Halpen (2003)，第 3.8 节）。这使得推断变得困难。然而，很少有研究比较基于模糊的系统和概率系统。

模糊逻辑应用的例子

汽车和其他车辆子系统，例如自动变速器、ABS 和巡航控制（例如东京单轨铁路）
空调
《指环王》电影中使用的庞大引擎，帮助展示了规模巨大的军队创造出随机但有序的运动
相机
数字图像处理，例如边缘检测
电饭煲
洗碗机
电梯
洗衣机和其他家用电器
电子游戏人工智能
论坛和聊天室中的语言过滤器，用于过滤掉攻击性文字
遥感中的模式识别
模糊逻辑也已被集成到一些微控制器和微处理器中，例如飞思卡尔 68HC12。

模糊逻辑的应用

模糊集理论定义了模糊集上的模糊运算符。应用此方法的问题在于可能不知道适当的模糊运算符。出于这个原因，模糊逻辑通常使用 IF/THEN 规则，或等效的结构，例如模糊关联矩阵。

规则通常以以下形式表达
IF 变量 IS 集合 THEN 动作

例如，一个非常简单的使用风扇的温度调节器可能如下所示
IF 温度 IS 非常冷 THEN 停止风扇
IF 温度 IS 冷 THEN 降低风扇速度
IF 温度 IS 正常 THEN 维持水平
IF 温度 IS 热 THEN 加快风扇速度

请注意，没有“ELSE”。所有规则都会被评估，因为温度可能同时“冷”和“正常”，但程度不同。

布尔逻辑的 AND、OR 和 NOT 运算符存在于模糊逻辑中，通常定义为最小值、最大值和补集；当它们以这种方式定义时，它们被称为扎德运算符，因为它们最初是在扎德的原始论文中这样定义的。所以对于模糊变量 x 和 y

NOT x = (1 - truth(x))

x AND y = minimum(truth(x), truth(y))

x OR y = maximum(truth(x), truth(y))

还有一些其他运算符，它们在本质上更具语言性，被称为修饰符，可以应用于它们。这些通常是副词，例如“非常”或“有点”，它们使用数学公式来修改集合的含义。

在应用中，Prolog 编程语言非常适合实现模糊逻辑，因为它提供了建立“规则”数据库的功能，这些规则可以被查询以推断逻辑。这种类型的编程被称为逻辑编程。

一旦定义了模糊关系，就可以开发模糊关系数据库。第一个模糊关系数据库 FRDB 出现在 Maria Zemankova 的论文中。之后，出现了一些其他模型，例如 Buckles-Petry 模型、Prade-Testemale 模型、Umano-Fukami 模型或 J.M. Medina、M.A. Vila 等人的 GEFRED 模型。在模糊数据库的背景下，已经定义了一些模糊查询语言，突出显示了 P. Bosc 等人的 SQLf 和 J. Galindo 等人的 FSQL。这些语言定义了一些结构，以便在 SQL 语句中包含模糊方面，例如模糊条件、模糊比较器、模糊常量、模糊约束、模糊阈值、语言标签等等。

其他示例

如果一个男人身高 1.8 米，则认为他很高。

如果男性为真且身高 >= 1.8 那么 is_tall 为真；is_short 为假。

模糊规则不会在高和矮之间进行严格区分，这不是很现实。

如果身高 <= 中等男性那么 is_short 为有点同意。
如果身高 >= 中等男性那么 is_tall 为有点同意。

在模糊情况下，不存在 1.83 米这样的高度，但存在模糊值，例如以下分配

矮个子男性 = [0, 1.3] 米
个子男性 = (1.3, 1.5]
中等男性 = (1.5, 1.8]
高个子男性 = (1.8, 2.0]
巨人男性 > 2.0 米

对于结果，也不只有两个值，而是五个，例如

不同意 = 0
有点同意 = 1
有点同意 = 2
非常同意 = 3
完全同意 = 4

在二进制或“清晰”的情况下，身高为 1.79 米的人被认为是矮个子。如果另一个人身高为 1.8 米或 2.25 米，则这些人被认为是高个子。

清晰的示例有意与模糊的示例不同。我们没有在前提中放入

如果男性 >= 有点同意并且 ...

因为性别通常被认为是二元信息。所以，它不像身高那样复杂。

形式化模糊逻辑

在数学逻辑中，有几个形式系统对上述“模糊逻辑”的概念进行建模；它们大多数属于所谓的 t-范数模糊逻辑。请注意，它们使用与上面提到的扎德运算符不同的运算符集。

命题模糊逻辑

最重要的命题模糊逻辑是

基本命题模糊逻辑 BL 是一个逻辑公理化，其中合取由连续的 |t-范数定义，蕴涵由 t-范数的残差定义。它的模型对应于 BL-代数。
Łukasiewicz 模糊逻辑是基本模糊逻辑的一个特例，其中合取是 Łukasiewicz t-范数。它具有基本逻辑的公理，再加上双重否定公理（因此它不是直觉逻辑），它的模型对应于 MV-代数。
Gödel 模糊逻辑是基本模糊逻辑的一个特例，其中合取是 Gödel t-范数。它具有基本逻辑的公理，再加上合取幂等公理，它的模型被称为 G-代数。
乘积模糊逻辑是基本模糊逻辑的一个特例，其中合取是乘积 t-范数。它具有基本逻辑的公理，再加上另一个公理，它的模型被称为乘积代数。
单调 t-范数逻辑 MTL 是基本模糊逻辑 BL 的一个泛化，其中合取由左连续的 t-范数实现。它的模型（MTL-代数）是预线性交换有界积分残差格。
有理 Pavelka 逻辑是多值逻辑的泛化。它是 Łukasiewicz 模糊逻辑的扩展，包含额外的常量。

所有这些逻辑都包含传统的命题逻辑（它的模型对应于布尔代数）。

谓词模糊逻辑

这些通过添加全称量词和存在量词来扩展上述模糊逻辑，类似于谓词逻辑从命题逻辑中创建的方式。t-范数模糊逻辑中全称量词和存在量词的语义分别是量化子公式实例的真值度的下确界和上确界。

模糊逻辑的有效性

“可判定子集”和“递归可枚举子集”的概念是经典数学和经典逻辑的基本概念。然后，就会出现将这些概念适当扩展到模糊集理论的问题。E.S. Santos 在模糊图灵机、马尔可夫正规模糊算法和模糊程序的概念上提出了第一个建议。随后，L. Biacino 和 G. Gerla 提出了以下定义，其中Ü 表示 [0,1] 中的有理数集。一个集合S 的模糊子集 μ : S $\rightarrow$ [0,1]是递归可枚举的，如果存在递归映射h : S×N $\rightarrow$ Ü 使得对于S 中的每个x，函数h(x,n) 随着n 的增加而增加，并且 μ(x) = lim h(x,n)。如果 μ 和它的补集 –μ 都是递归可枚举的，那么我们说 μ 是可判定的。G. Gerla 在一篇论文中提出了将这种理论扩展到 L-子集的一般情况。提出的定义与模糊逻辑很好地相关。事实上，以下定理成立（只要模糊逻辑的演绎装置满足一些明显的有效性属性）。

定理。 任何可公理化的模糊理论都是递归可枚举的。特别是，尽管有效公式的清晰集通常不是递归可枚举的，但逻辑真公式的模糊集是递归可枚举的。此外，任何可公理化和完备的理论都是可判定的。

为了支持模糊逻辑的丘奇论题，即模糊子集的递归可枚举性概念是合适的，这是一个悬而未决的问题。为此，需要对模糊语法和模糊图灵机的概念进行进一步研究（例如，参见 Wiedermann 的论文）。另一个悬而未决的问题是从这个概念开始，为模糊逻辑找到 Gödel 定理的扩展。

参考书目

Von Altrock, Constantin (1995). 模糊逻辑和神经模糊应用解释. Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-368465-2.
Biacino, L. (2002). "模糊逻辑、连续性和有效性". 数学逻辑档案. 41 (7): 643–667. doi:10.1007/s001530100128. ISSN 0933-5846. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
Cox, Earl (1994). 模糊系统手册：构建、使用和维护模糊系统的实践指南. Boston: AP Professional. ISBN 0-12-194270-8.
Elkan, C. (1994). "模糊逻辑的悖论式成功". IEEE Expert. 9 (4): 3–8. doi:10.1109/64.336150. ISSN 0885-9000. {{cite journal}}: 引用中存在空的未知参数：|coauthors= (帮助). 来自 Elkan 的主页.
Gerla, Giangiacomo (2006). "有效性和多值逻辑". Journal of Symbolic Logic. 71 (1): 137–162. ISSN 0022-4812. {{cite journal}}: 引用中存在空的未知参数：|coauthors= (帮助)
Hájek, Petr (1998). 模糊逻辑的元数学. 多德雷赫特: 克鲁维尔. ISBN 0792352386.
Hájek, Petr (1995). "模糊逻辑与算术层次结构". Fuzzy Sets and Systems. 3 (8): 359–363. doi:10.1016/0165-0114(94)00299-M. ISSN 0165-0114. {{cite journal}}: 引用中存在空的未知参数：|coauthors= (帮助)
Halpern, Joseph Y. (2003). 关于不确定性的推理. 马萨诸塞州剑桥: 麻省理工学院出版社. ISBN 0-262-08320-5.
Höppner, Frank (1999). 模糊聚类分析：分类、数据分析和图像识别方法. 纽约: 约翰·威利. ISBN 0-471-98864-2. {{cite book}}: 未知参数 |coauthors= 被忽略 (|author= 建议) (帮助)
Ibrahim, Ahmad M. (1997). 应用模糊电子学导论. 新泽西州恩格伍德峭壁: 普伦蒂斯·霍尔. ISBN 0-13-206400-6. {{cite book}}: 引用中存在空的未知参数：|coauthors= (帮助)
Klir, George J. (1988). 模糊集、不确定性和信息. 新泽西州恩格伍德峭壁: 普伦蒂斯·霍尔. ISBN 0-13-345984-5. {{cite book}}: 未知参数 |coauthors= 被忽略 (|author= 建议) (帮助)
Klir, George J. (1997). 模糊集理论：基础和应用. 新泽西州恩格伍德峭壁: 普伦蒂斯·霍尔. ISBN 0133410587. {{cite book}}: 未知参数 |coauthors= 被忽略 (|author= 建议) (帮助)
Klir, George J. (1995). 模糊集和模糊逻辑：理论与应用. 新泽西州上鞍河: 普伦蒂斯·霍尔 PTR. ISBN 0-13-101171-5. {{cite book}}: 未知参数 |coauthors= 被忽略 (|author= 建议) (帮助)
Kosko, Bart (1993). 模糊思维：模糊逻辑的新科学. 纽约: 海波里昂. ISBN 0-7868-8021-X.
Montagna, F. (2001). "量化模糊逻辑中的三个复杂性问题". Studia Logica. 68 (1): 143–152. doi:10.1023/A:1011958407631. ISSN 0039-3215. {{cite journal}}: 引用中存在空的未知参数：|coauthors= (帮助)
Mundici, Daniele (1999). 多值推理的代数基础. 多德雷赫特: 克鲁维尔学术出版社. ISBN 0-7923-6009-5. {{cite book}}: 未知参数 |coauthors= 被忽略 (|author= 建议) (帮助)
Novák, Vilém (1999). 模糊逻辑的数学原理. 多德雷赫特: 克鲁维尔学术出版社. ISBN 0-7923-8595-0. {{cite book}}: 未知参数 |coauthorsr= 被忽略 (帮助)
Passino, Kevin M. (1998). 模糊控制. 波士顿：Addison-Wesley. ISBN 020118074X. {{cite book}}: 未知参数 |coauthors= 被忽略 (|author= 建议) (帮助)
Scarpellini, Bruno (1962). "Die Nichaxiomatisierbarkeit des unendlichwertigen Prädikatenkalküls von Łukasiewicz". 符号逻辑杂志. 27 (2): 159–170. doi:10.2307/2964111. ISSN 0022-4812. {{cite journal}}: 引用包含空未知参数：|coauthors= (帮助)
Wiedermann, J. (2004). "Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines". Theor. Comput. Sci. 317: 61–69. {{cite journal}}: 引用包含空未知参数：|coauthors= (帮助)
Yager, Ronald R. (1994). 模糊建模与控制精要. 纽约：Wiley. ISBN 0-471-01761-2. {{cite book}}: 未知参数 |coauthors= 被忽略 (|author= 建议) (帮助)
Zadeh, L.A. (1968). "Fuzzy algorithms". 信息与控制. 12 (2): 94–102. doi:10.1016/S0019-9958(68)90211-8. ISSN 0019-9958. {{cite journal}}: 引用包含空未知参数：|coauthors= (帮助)
Zadeh, L.A. (1965). "Fuzzy sets". 信息与控制. 8 (3): 338-353. doi:10.1016/S0019-9958(65)90241-X. ISSN 0019-9958. {{cite journal}}: 引用包含空未知参数：|coauthors= (帮助); |pages= 中位置 5 的软连字符 (帮助)
Zemankova-Leech, M. (1983). "Fuzzy Relational Data Bases". 博士论文. 佛罗里达州立大学. {{cite journal}}: 引用期刊需要 |journal= (帮助)
Zimmermann, H. (2001). 模糊集理论及其应用. 波士顿：Kluwer Academic Publishers. ISBN 0-7923-7435-5.

外部链接

更多文章

形式模糊逻辑 - Citizendium 上的详细文章
模糊逻辑 - Scholarpedia 上的文章
模糊逻辑 - 斯坦福哲学百科全书上的文章
面向“普通人”的模糊逻辑
模糊逻辑应用 PC AI 2002 年 3/4 月模糊规则入门
模糊数学 - 模糊逻辑入门级介绍。

链接页面

关于 FSQL 的网页: 关于 FSQL 的参考资料和链接

软件和工具

免费教育软件和应用说明
InrecoLAN FuzzyMath, OpenOffice.org Calc 的模糊逻辑插件
JFuzzyLogic: 开源模糊逻辑包 + FCL (sourceforge, java)
基于 Metarule 的开源模糊逻辑推理引擎和数据挖掘 Web 服务
开源软件“mbFuzzIT” (Java)

教程

示例应用