费马大定理/附录

本附录收集了一些证明和深入研究了某些数学概念，这些概念对于深入研究本书的某些方面可能很有趣。它力求保持简单的方法，但证明是正确的，在某些情况下，有必要借助一些不直接的概念和段落，这些概念和段落已在可能的情况下进行说明和澄清。

勾股定理

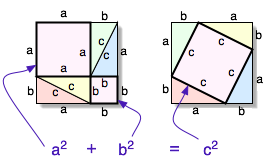
作为数学史上最著名的定理之一，存在着许多证明，包括天文学家、股票经纪人，甚至列奥纳多·达·芬奇的证明。也许，它与二次互反律一起，争夺了具有最多绝对证明的定理的奖项。它将以图形方式进行证明，仅使用初等几何的概念。勾股的证明将不予引用，因为它非常复杂，并不直观。

证明非常简单，从图形中可以看出，首先构造一个由四个三角形和两个正方形组成的正方形，一个边长为a，另一个边长为b。正方形的面积是通过将边乘以自身来计算的，或者用现代符号表示，面积是边升到二次方。因此，大正方形的面积是a²和b²的平方值之和加上四个三角形的面积之和。在第二个正方形中，我们再次有四个三角形和一个面积为c²的正方形。四个三角形既存在于等式左侧，也存在于右侧，因此可以消除。因此，等式中剩下

a² + b² = c²

如你所愿证明。需要注意的是，证明是通用的，实际上涵盖了所有可能的直角三角形，因为证明中没有使用数字，而只使用了通用的线段长度a、b和c。证明仅取决于三角形是直角三角形以及使用的是欧几里得几何这一事实。即使如上所述，这个定理有很多几何证明，这只是一个小型画廊，实际上还有纯粹的代数证明、使用复数的证明，甚至以十四行诗形式写成的证明。

算术基本定理

算术基本定理指出，每个不等于 1 的自然数都承认唯一的一个素数分解，而不考虑因子的顺序。（排除 1 是因为它没有素数因子。）这个定理是加布里埃尔·拉梅和奥古斯丁·路易斯·柯西证明的基础，正如前面所说，它通常不适用于复数，因此不能用于费马定理，但鉴于它的重要性，决定将其证明包含在附录中。对于“小”自然数，该语句很容易验证：很容易发现 70 等于2 × 5 × 7，而 100 等于2 × 2 × 5 × 5 或2² × 5²，此外，很容易验证对于这些数字，不存在其他素数分解。相反，一般的证明要长得多：这里摘录了它的一部分。它处理的是反证法：也就是说，它从与语句相反的假设出发，以便能够证明它是不成立的。

假设存在某个可以以多种方式分解成素因子的数字，并称其为最小的m。首先证明，给定m的两个分解，第一个分解中出现的素数与第二个分解中出现的素数都不相同。事实上，它们是两个不同的分解

[1]

m=p_{1}p_{2}p_{3}\dots p_{s}

[2]

m=q_{1}q_{2}q_{3}\dots q_{t}

其中p_i和q_j是素数。（注意：在一个分解中，自然地可以存在重复的因子：例如，100 = 2 × 2 × 5 × 5）。如果存在相同的因子p_h = q_k，我们可以用这个因子除以m，得到一个比m小的数字m'，它本身也会有两种不同的分解。在这一点上，我们知道p₁与q₁不同；不失一般性地，我们可以假设p₁ < q₁。然后我们把

[3]

n=(q_{1}-p_{1})q_{2}q_{3}\dots q_{t}

显然，n < m，因为[3]可以写成

[4]

n=q_{1}q_{2}q_{3}\dots q_{t}-p_{1}q_{2}q_{3}\dots q_{t}=m-p_{1}q_{2}q_{3}\dots q_{t}\;\!

.

现在我们证明n至少有两种不同的分解。我们首先考虑n的第一个因子q₁ - p₁是否可以是素数；如果它不是素数，我们假设对它进行分解。由此得到的n的分解在其因子中不包含p₁。事实上，从证明的第一部分，我们知道p₁与q₂, q₃, ..., q_t不同；但是，它不能出现在q₁ - p₁的最终分解中。事实上，如果这种情况发生，将意味着

q_{1}-p_{1}=p1\cdot b\Rightarrow q_{1}=p_{1}(1+b)

因此，q₁ 可以被 p₁ 整除，但这不可能，因为 q₁ 是一个质数。现在，我们用 [1] 中的值替换 [4] 中的 m，得到

[5]

n=p_{1}p_{2}p_{3}\dots p_{s}-p_{1}q_{2}q_{3}\dots q_{t}\rightarrow n=p_{1}(p_{2}p_{3}\dots p_{s}-q_{2}q_{3}\dots q_{t})

无论 [5] 中第二个因子的分解方式如何，我们都将得到一个包含 p₁ 的 n 的分解，因此它与 [3] 中的分解不同，这与 m 是唯一一个具有多种分解方式的最小数的假设相矛盾。因此定理得证。

归纳原理

归纳原理指出：

如果 $U$ 是自然数集 $\mathbb {N}$ 的一个子集，并且满足以下两个性质：

$U$ 包含 $0$ ,

每当 $U$ 包含一个数 $n$ 时， $U$ 也包含其后继数 $n+1$ ,

那么 $U$ 与所有自然数集 $\mathbb {N}$ 重合。

这通常在 Peano 公理中找到，并为数学各个领域中的证明提供了强有力的工具。由于许多数学家试图证明费马大定理的基准情况，然后将解推广到包括后续情况，因此在本书中，我们偶尔会回顾这个原理。

归纳法证明

为了证明一个包含自然数 $n$ 的断言 $P(n)$ 对所有 $n\in \mathbb {N}$ 有效，我们需要用以下方式使用归纳原理：

我们设 $U=\{n\in \mathbb {N} :{\mbox{vale }}P(n)\}$ ,

首先，证明 $P(0)$ 是有效的，也就是说 $0$ 属于自然数集 $U$ ，对于该集合中的所有 $n$ ，命题 $P(n)$ 是有效的；
假设命题 $P(n)$ 对于任意一个 $n$ 是有效的，并从这个假设出发，证明命题 $P(n+1)$ 也是有效的（即 $n\in U\Rightarrow n+1\in U$ ）。

因此，可以得出结论，使得命题 $P(n)$ 有效的数的集合 $U$ 与所有自然数的集合一致。步骤 1 通常被称为 **归纳基础**，步骤 2 被称为 **归纳步骤**。

以下是一种直观的方式来理解这种类型的证明：如果我们有一个关于基本情况 $P(0)$ 的证明，以及一个关于归纳步骤 $P(n)\Rightarrow P(n+1)$ 的证明，那么我们显然可以使用这些证明来证明 $P(1)$ ，方法是在 $P(0)$ （基本情况）和 $P(0)\Rightarrow P(1)$ （它是当 $n=0$ 时归纳步骤的特例）上应用逻辑规则肯定前件，然后我们可以证明 $P(2)$ ，因为我们现在是在 $P(1)$ 和 $P(1)\Rightarrow P(2)$ 上应用肯定前件，因此对于 $P(3)$ ， $P(4)$ ，等等... 此时很明显，我们可以用有限步（最终会非常长）来产生 $P(n)$ 的证明，对于任何自然数 $n$ ，由此我们推断出 $P(n)$ 对于每个 $n\in \mathbb {N}$ 都是真的。

一个例子

我们将证明以下公式是有效的

对于每个 $n\in \mathbb {N}$ ： $0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$

在这种情况下，我们有 $P(n)\quad \equiv \quad 0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$ .

归纳基础: 我们需要证明断言 $P(n)$ 在 $n=0$ 时为真。因此，代入后，有 $0={\frac {0\cdot 1}{2}}$ ，实际上，这项工作非常简单，我们只需要进行一个基本的计算。
归纳步骤: 我们需要证明对于任何n，蕴涵关系 $P(n)\Rightarrow P(n+1)$ 是有效的，也就是说，代入后

0+1+2+3+4+...+n={\frac {n(n+1)}{2}}\quad \Rightarrow \quad 0+1+2+3+4+...+n+(n+1)={\frac {(n+1)((n+1)+1)}{2}}

因此，我们需要假设

P(n)\quad \equiv \quad 0+1+2+3+4+...+n={\frac {n(n+1)}{2}}

,

在此等式基础上进行推导，最终得到与 $n+1$ 类似的等式：例如，我们可以将 $n+1$ 添加到等式P(n)的两边

0+1+2+3+4+...+n+(n+1)={\frac {n(n+1)}{2}}+(n+1)

,

然后进行一些简单的代数运算

0+1+2+3+4+...+n+(n+1)={\frac {n(n+1)}{2}}+{\frac {2(n+1)}{2}}

,

0+1+2+3+4+...+n+(n+1)={\frac {(n+1)(n+2)}{2}}

,

0+1+2+3+4+...+n+(n+1)={\frac {(n+1)((n+1)+1)}{2}}

而这个最终等式正是 $P(n+1)$ 。这完成了归纳步骤的证明。

因此，在证明了归纳基底和归纳步骤之后，我们可以得出结论（根据归纳原理），对于每一个 $P(n)$ 都必须成立 $n\in \mathbb {N}$ 。 $\square$

模算术

模算术（有时称为时钟算术，因为 12 或 24 小时周期内的计算是基于这种原理的）是数学的一个重要分支。它在密码学、数论（特别是素数的研究）中有着广泛的应用，也是许多最常见的算术和代数运算的基础。它处理一个整数算术系统，在这个系统中，数字每次达到一个特定数字 *n* 的倍数时就会“循环自身”，这个特定数字 *n* 被称为模数。模算术是由卡尔·弗里德里希·高斯在他的著作《算术研究》中正式引入的，该书于 1801 年出版。模算术基于 **模 *n* 同余** 的概念。给定三个整数 *a*、*b*、*n*，其中 *n*≠0，我们说 *a* 和 *b* 模 *n* 同余，如果它们的差（*a−b*）是 *n* 的倍数。在这种情况下，我们写