“水轮机 ”一词源于希腊语tyrbē (τύρβη) ,意思是湍流 。水轮机由Gustaf de Laval 于1882年发明。现代水轮机的示范由查尔斯·帕森斯爵士 于1884年发明。水轮机是一种机器,它利用流体的动能,通过设计的机构转化为机械能 。水轮机由连接到轴上的多个叶片组成,轴通常用来驱动发电机。水轮机的工作原理是,水轮机的叶片被运动的流体(例如蒸汽、水、气体等)旋转,从而旋转连接到使用这种旋转能量的装置的轴。
根据水轮机的工作类型,可以将其分为两种:
上图是冲击式水轮机的模型。下图是反作用式水轮机的模型。 冲击式水轮机 反作用式水轮机 压力头 速度头 可压缩流体 不可压缩流体 在冲击式水轮机中,首先将所使用的流体通过专门设计的喷嘴 ,将其压力头转化为速度头 。然后,从喷嘴喷出的所需流体流束撞击到弯曲的(水桶形状的 )叶片上。该流体的速度头因此被用来为旋转叶片和轴提供动量。叶片的设计方式使得流体从喷嘴撞击叶片的方向改变其方向并离开叶片。在此过程中产生的冲击力被用来为叶片提供动量。这就是为什么我们把这种类型的水轮机称为冲击式水轮机 。 冲击式水轮机最常见的例子是佩尔顿轮
佩尔顿轮是一种水轮机。它是冲击式水轮机 中最著名的例子。莱斯特·艾伦·佩尔顿在19世纪70年代发明了这种水轮机。这种水轮机利用的是流动的水的能量。早些时候也制造了许多冲击式水轮机,但它们不像佩尔顿轮那样高效。这是因为水离开水轮机时仍然带走了大部分动能,因此能量利用率较低。但是佩尔顿对此进行了研究,并通过改变叶片的几何形状找到了一个巧妙的解决方案。它的设计方式使得即使当轮缘的速度等于喷嘴中水的速度的一半时,流出的水也几乎没有剩余能量。这样,大部分能量都被充分利用了。这使得它成为一种非常高效的水轮机设计。
所需功率可以根据需要进行调节。因此,这种需求可以通过一个矛头机制来满足。这可以通过调节矛头的位置来实现。如果功率需求较高,则将矛头移向喷嘴的出口,如果功率需求较低,则将矛头移开喷嘴的出口。因此,功率需求与水流速同步。喷嘴上安装了一个分流器。特殊的叶片设计使水在 180 o {\displaystyle 180^{o}} 2 n d {\displaystyle 2^{nd}} 180 o {\displaystyle 180^{o}}
最大化能量提取
叶片提取的功率, P = F i m p u l s e × V b u c k e t {\displaystyle P=F_{impulse}\times V_{bucket}}
分析两种情况
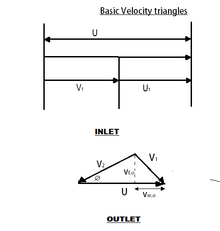
叶片保持静止 :会产生很大的冲击力,但由于叶片保持静止,因此提取的功率为零。叶片的速度与射流速度相同 :如果发生这种情况,则水射流将无法撞击叶片,导致冲击力为零。因此,再次没有能量被提取。入口和出口处的速度三角形 水施加的力= m ˙ ( v w , i − v w , o ) {\displaystyle {\dot {m}}(v_{w,i}-v_{w,o})}
功率= m ˙ ( v w , i − v w , o ) U 1 {\displaystyle {\dot {m}}(v_{w,i}-v_{w,o})U_{1}}
水力效率, η {\displaystyle \eta } ( v w , i − v w , o ) U 1 g U 2 2 g {\displaystyle {(v_{w,i}-v_{w,o}){U_{1} \over g} \over {U^{2} \over 2g}}}
要获得最大效率,
v w , i = U = V 1 + U 1 {\displaystyle v_{w,i}=U=V_{1}+U_{1}}
v w , o = U 1 − V r , o cos ϕ {\displaystyle v_{w,o}=U_{1}-V_{r,o}\cos {\phi }}
因此, P = m ˙ ( v r , i + v r , o cos ϕ ) {\displaystyle P={\dot {m}}(v_{r,i}+v_{r,o}\cos {\phi })}
假设,叶片沿摩擦阻力=0
( v r , i = v r , o ) {\displaystyle (v_{r,i}=v_{r,o})}
因此, P = m ˙ U 1 ( U − U 1 ) ( 1 + cos ϕ ) {\displaystyle P={\dot {m}}U_{1}(U-U_{1})(1+\cos {\phi })}
为了使P最大化, d P d U 1 = 0 {\displaystyle {\frac {\mathrm {d} P}{\mathrm {d} U_{1}}}=0}
因此, U = 2 U 1 {\displaystyle U=2U_{1}}
Daugherty 对佩尔顿水轮性能的分析
提供给涡轮机的净水头h可通过以下公式计算得出:
h = h ″ + k V 2 2 2 g + m V 2 2 2 g + k ″ V 2 2 2 g {\displaystyle h=h''+k{\frac {V_{2}^{2}}{2g}}+m{\frac {V_{2}^{2}}{2g}}+k''{\frac {V_{2}^{2}}{2g}}}
h ″ {\displaystyle h''}
k V 2 2 2 g {\displaystyle k{\frac {V_{2}^{2}}{2g}}}
m V 2 2 2 g {\displaystyle m{\frac {V_{2}^{2}}{2g}}}
k ″ V 2 2 2 g {\displaystyle k''{\frac {V_{2}^{2}}{2g}}}
佩尔顿水斗内水流速度分量的示意图 转轮利用的热量,
h ″ = l g ( u 1 v 1 − u 2 v 2 cos α 2 ) {\displaystyle h''={l \over g}(u_{1}v_{1}-u_{2}v_{2}\cos \alpha _{2})}
利用转轮中水流相对运动的能量方程。
转轮内的总水头损失 = ( z 1 + v 1 2 2 g + p 1 ρ g ) − ( z 2 + v 2 2 2 g + p 2 ρ g ) {\displaystyle ={\Bigg (}z_{1}+{\frac {v_{1}^{2}}{2g}}+{\frac {p_{1}}{\rho g}}{\Bigg )}-{\Bigg (}z_{2}+{\frac {v_{2}^{2}}{2g}}+{\frac {p_{2}}{\rho g}}{\Bigg )}}
利用相对速度和公式 1 & 2,我们得到,
( z 1 + V 1 2 − U 1 2 2 g + p 1 ρ g ) − ( z 2 + V 2 2 − U 2 2 2 g + p 2 ρ g ) {\displaystyle {\Bigg (}z_{1}+{\frac {V_{1}^{2}-U_{1}^{2}}{2g}}+{\frac {p_{1}}{\rho g}}{\Bigg )}-{\Bigg (}z_{2}+{\frac {V_{2}^{2}-U_{2}^{2}}{2g}}+{\frac {p_{2}}{\rho g}}{\Bigg )}}
假设 z 1 = z 2 , p 1 = p 2 , u 1 = u 2 {\displaystyle z_{1}=z_{2},p_{1}=p_{2},u_{1}=u_{2}}
V 2 = V 1 1 + k = v 1 − U 1 1 + k {\displaystyle V_{2}={\frac {V_{1}}{\sqrt {1+k}}}={\frac {v_{1}-U_{1}}{\sqrt {1+k}}}}
水斗上的切向力, F t = m ˙ ( U − u 2 − V 2 cos β ) {\displaystyle F_{t}={\dot {m}}{\bigg (}U-u_{2}-V_{2}\cos \beta {\bigg )}}
F t = m ˙ ( 1 − cos β 2 1 + k ) ( V 1 − U 1 ) {\displaystyle F_{t}={\dot {m}}{\Bigg (}1-{\frac {\cos \beta _{2}}{\sqrt {1+k}}}{\Bigg )}(V_{1}-U_{1})}
P = m ˙ ( 1 − cos β 2 1 + k ) ( V 1 − U 1 ) U 1 {\displaystyle P={\dot {m}}{\Bigg (}1-{\frac {\cos \beta _{2}}{\sqrt {1+k}}}{\Bigg )}(V_{1}-U_{1})U_{1}}
(注意:在实际情况下,不能假设 U = v 1 {\displaystyle U=v_{1}}