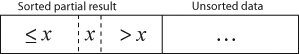GCSE 计算机科学/排序算法

排序算法是所有 GCSE 计算机科学课程的一部分。即使课程不需要知道以下排序算法中的一种或多种的名称和定义，也需要能够在特定情况下理解和使用这些算法。

冒泡排序

哪些课程？ AQA 3.1.4，Ed 1.1.8，OCR 2.1

冒泡排序是一种排序算法，它不断地遍历一个列表，交换项目，直到它们按正确的顺序出现。

冒泡排序是一种简单的排序算法，它的工作原理是反复遍历要排序的列表，比较每一对元素，如果它们顺序错误就交换它们。重复遍历列表，直到不需要交换，这表明列表已经排序。该算法之所以得名，是因为较大的元素会“冒泡”到列表的顶部。这是一种非常慢的排序数据方法，在工业中很少使用。还有更快排序算法，比如插入排序，我们将在后面讨论。

逐步示例

让我们以数字数组“5 1 4 2 8”为例，使用冒泡排序算法将数组从最小数字排序到最大数字。在每一步中，以粗体显示的元素正在被比较。

第一遍
( 5 1 4 2 8 ) $\to$ ( 1 5 4 2 8 ), 这里，算法比较了前两个元素，并交换了它们，因为 5 > 1
( 1 5 4 2 8 ) $\to$ ( 1 4 5 2 8 ), 然后比较了第二个和第三个元素，并交换了它们，因为 5 > 4
( 1 4 5 2 8 ) $\to$ ( 1 4 2 5 8 ), 交换，因为 5 > 2
( 1 4 2 5 8 ) $\to$ ( 1 4 2 5 8 ), 现在，由于这些元素已经按顺序排列（8 > 5），算法不会交换它们。
算法已经到达数字列表的末尾，最大数字 8 已经冒泡到顶部。现在它重新开始。

第二遍
( 1 4 2 5 8 ) $\to$ ( 1 4 2 5 8 ), 不需要交换
( 1 4 2 5 8 ) $\to$ ( 1 2 4 5 8 ), 交换，因为 4 > 2
( 1 2 4 5 8 ) $\to$ ( 1 2 4 5 8 ), 不需要交换
( 1 2 4 5 8 ) $\to$ ( 1 2 4 5 8 ), 不需要交换
现在，数组已经排序，但我们的算法不知道它是否完成了。算法需要一个完整的遍历，没有任何交换才能知道它已经排序。
第三遍
( 1 2 4 5 8 ) $\to$ ( 1 2 4 5 8 )
( 1 2 4 5 8 ) $\to$ ( 1 2 4 5 8 )
( 1 2 4 5 8 ) $\to$ ( 1 2 4 5 8 )
( 1 2 4 5 8 ) $\to$ ( 1 2 4 5 8 )
最后，数组被排序，算法可以终止。

练习

1) Sort the following lists using a bubble sort. How many passes are needed?

(a) 按字母顺序排序

Henry, Cat, George, Mouse

答案

Cat, George, Henry, Mouse (Pass 1)
Cat, George, Henry, Mouse (Pass 2)
2 passes

(b) 按字母顺序排序

G, C, N, A, P, C

答案

C, G, A, N, C, P (Pass 1)
C, A, G, C, N, P (Pass 2)
A, C, C, G, N, P (Pass 3)
A, C, C, G, N, P (Pass 4)
4 passes

(c) 按数字顺序排序

12, 56, 0, 23, 10

答案

12, 0, 23, 10, 56 (Pass 1)
0, 12, 10, 23, 56 (Pass 2)
0, 10, 12, 23, 56 (Pass 3)
0, 10, 12, 23, 56 (Pass 4)
4 passes

2) 显示以下两遍之后的排序结果

(a) 按字母顺序排序

Emu, Shrike, Gull, Badger 

答案

Emu, Gull, Badger, Shrike (Pass 1)
Emu, Badger, Gull, Shrike (Pass 2)

(b) 按数字顺序排序

99, 45, 32, 56, 12

答案

45, 32, 56, 12, 99 (Pass 1)
32, 45, 12, 56, 99 (Pass 2)

插入排序

哪些课程？ AQA 3.1.4，Ed 1.1.8，OCR 2.1

插入排序的示例。检查每个元素并将它们按正确顺序放入已排序的列表中。

不幸的是，冒泡排序是一种非常慢的排序数据方法，在工业中很少使用。我们现在将介绍一种更快的算法，插入排序。

插入排序 是一种简单的排序算法：一种比较排序，其中排序后的数组（或列表）一次构建一个条目。对于大型列表来说，它比更高级的算法（例如下面将介绍的归并排序）效率要低得多。但是，插入排序具有一些优势

• 实现简单
• 对小型数据集效率高
• 运行时使用固定数量的内存

插入排序需要使用两个数组，一个有序，一个无序。算法的每次重复都将一个项目从无序列表移动到有序列表中的排序位置，直到无序列表中没有元素。

排序通常是在原地进行的，不需要额外的内存。经过k次迭代后的结果数组具有以下属性：前k + 1个条目已排序。在每次迭代中，输入的第一个剩余条目被删除，插入到结果中的正确位置，从而扩展结果

变为

每个大于x的元素在与x比较时被复制到右侧。

对一个 30 元素数组进行插入排序的动画。请注意，有序数组（左侧）如何慢慢地消耗无序数组（右侧），直到整个数据集被排序

示例：插入排序 下表显示了对序列 {5, 7, 0, 3, 4, 2, 6, 1} 进行排序的步骤。对于每次迭代，插入元素移动的位置数都显示在括号中。总共 17 步。 5 7 0 3 4 2 6 1 (0) 5 7 0 3 4 2 6 1 (0) 0 5 7 3 4 2 6 1 (2) 0 3 5 7 4 2 6 1 (2) 0 3 4 5 7 2 6 1 (2) 0 2 3 4 5 7 6 1 (4) 0 2 3 4 5 6 7 1 (1) 0 1 2 3 4 5 6 7 (6) 5 7 0 3 4 2 6 1 (0) 5 7 0 3 4 2 6 1 (0) 0 5 7 3 4 2 6 1 (2) 0 3 5 7 4 2 6 1 (2) 0 3 4 5 7 2 6 1 (2) 0 2 3 4 5 7 6 1 (4) 0 2 3 4 5 6 7 1 (1) 0 1 2 3 4 5 6 7 (6)

练习：插入排序 描述插入排序的过程 答案 插入排序是一种简单的排序算法：一种比较排序，其中排序后的数组（或列表）一次构建一个条目。 显示插入排序如何在以下无序数组上工作 9 6 7 1 2 答案 左侧排序部分用下划线表示 9 6 7 1 2 6 9 7 1 2 6 7 9 1 2 1 6 7 9 2 1 2 6 7 9 显示插入排序如何在以下无序数组上工作 G K L A J 答案 左侧排序部分用下划线表示 G K L A J G K L A J G K L A J A G K L J A G J K L

归并排序

哪些课程？ OCR 2.1