使用 XNA/数学物理/弹道学创建游戏

弹道学

当想到弹道学时，首先想到的可能是枪支和各种致命的子弹。但尤其是在游戏中，弹道学可能与任何类型的弹丸的运动有关，从球到香蕉，从椰子到火箭。弹道学有助于确定这些弹丸在运动过程中的行为方式以及它们的影响。本章将展示并解释游戏程序员在编程任何与弹丸相关的项目时需要了解的内容。

基本物理学

任何弹丸的运动都将受到其周围环境和它应该遵守的物理定律的很大影响。但是，重要的是要记住，游戏不需要设置在地球上，外星星球上的体验可能与我们所知的有效体验完全不同。因此，此处列出的公式和解释可能需要调整，以适应您打算让弹丸在其间移动的任何世界。

质量和重量

质量与重量是同一个东西，这是一个常见的误解。但物体的重量会根据其所处环境的变化而变化，而物体的质量将保持不变。重量（用 W 表示）定义为当 重力 影响质量时存在的力

$W=mg\,$ ，其中 g 是存在的重力，m 表示物体的质量

速度和加速度

速度描述了物体在一定时间内通过运动所覆盖的距离以及这种运动的方向。它是你汽车沿着高速公路行驶或子弹在空中呼啸而过的速度和方向。可能最常见的用来表示速度的单位是 km/h 和 m/s。h 和 s 表示一定的时间量，其中 h 代表小时，s 代表秒，km 和 m 代表公里和米，即在此时间间隔内行驶的距离。速度由一个向量定义，该向量指定运动方向，其绝对值为速度。

想象一个直直向上抛起的球，它在整个飞行过程中不会有相同的速度。它会慢下来，直到到达顶点，然后会再次加速。这被称为加速度。它是物体速度随时间变化的速率。牛顿第二运动定律表明，加速度取决于作用于物体上的力（例如，抛出球的手臂和手的力）以及物体的质量（例如，球）：$F=ma\,\implies a={\frac {F}{m}}$
该物体的加速度将与施加的力方向相同。加速度的单位是距离除以时间的平方，例如 km/s²。

重力

万有引力是作用于任何两个物体之间的力，将它们相互吸引。这种力取决于物体的质量以及它们之间的距离。计算这种力的通用公式如下所示
$F=G{\frac {m_{1}m_{2}}{r^{2}}}$ ，其中 $m_{1}$ 和 $m_{2}$ 是物体的质量，r 是距离，G 是万有引力常数
万有引力常数为： $G=6.67428\times 10^{-11}\ {\mbox{m}}^{3}\ {\mbox{kg}}^{-1}\ {\mbox{s}}^{-2}=6.67428\times 10^{-11}\ {\rm {N}}\,{\rm {(m/kg)^{2}}}$

当谈论地球的重力时，指的是由于存在的引力而使物体感受到的加速度。因此，重力不过是朝地球中心点的加速度。这就是为什么从高楼掉下的物体，会一直处于自由落体状态，直到被其他物体，例如地面，阻止。地球的重力定义如下：$g=G{\frac {m_{earth}}{r^{2}}}$，其中g是地球的重力，m是地球的质量，r是地球的半径。
地球表面的重力约等于9.8米/秒²。

阻力

阻力会影响物体在流体和气体中运动的速度。这种力与物体运动方向相反，因此会随着时间的推移降低物体速度。它取决于物体的质量和形状，以及流体的密度。由于弹道计算通常被简化，你可能最终不需要阻力。但是，你应该考虑你的弹丸所处的流体和气体，并调整缩放因子以获得合适的弹道。

弹丸运动

在游戏中，玩家所处的世界永远不是现实世界的百分百准确的呈现。因此，在编程弹丸运动时，更容易简化一些物理学，同时营造出弹丸至少在一定程度上符合人类玩家预期行为的错觉。无论是投球还是在水下发射鱼雷，弹丸在游戏中都有两种普遍的简化运动模式。这些运动可以进行调整和细化，以匹配特定弹丸的预期运动。

弹丸类

建议创建一个自己的弹丸类，其中包含所有特定于弹丸的变量，例如速度，以及用于操纵和计算弹道的函数。该类的基本框架可能看起来像这样

public class Projectile{

private Vector3 velocity;   //stores the direction and speed of the projectile
public Vector3 pos;         //current projectile position
private Vector3 prevPos;    //previous projectile position
private float totalTimePassed;         //time passed since start 
public bool bmoving = false;        //if the projectile is moving

///Constants
private const float GRAVITY = 9.8f;

    public void Start(Vector3 direction,int speed, Vector3 startPos){
        this.velocity = speed*Vector3.Normalize(direction);   
        this.pos = startPos;   //in the beginning the current position is the start position
        bmoving = true;
    }
     
    public void UpdateLinear(GameTime time){
        if(bmoving) LinearFlight(time);
    }
    
    public void UpdateArching(GameTime time){
        if(bmoving) ArchingFlight(time);
    }
}

首先，需要一些东西来触发弹丸的运动，例如玩家的鼠标点击。在该事件发生时，你创建一个弹丸类的新实例，并调用Start()以发射弹丸。你需要保留对该对象的引用，因为弹丸的位置将在每一帧进行更新，并且弹丸会被重新绘制。更新是通过调用UpdateLinear或UpdateArching函数完成的，具体取决于所需的弹道。新位置必须是用于在游戏世界中绘制弹丸的变换矩阵的一部分。

在Start方法中，方向向量被归一化，以确保在乘以速度时，结果是与初始向量方向相同且具有所需速度绝对值的向量。请记住，传递给Start函数的方向向量是发射弹丸的任何东西的瞄准向量。当我们假设瞄准是可变的时，它的绝对值基本上可以是任何东西。因此，这不能保证相同类型的弹丸以相同的速度移动，也不能允许玩家决定在弹丸释放之前施加在弹丸上的力，从而改变其速度。

如果你的弹丸形状具有明显的正面、末端和侧面，那么需要根据其弹道改变弹丸的方向。根据欧拉旋转定理，旋转矩阵的向量必须是单位向量，并且是正交的。对于线性弹道，我们可以简单地将归一化速度向量作为方向矩阵的向前向量，并相应地构建矩阵的向右向量和向上向量。但是，由于在使用拱形弹道时，弹丸的飞行方向会不断变化，因此更容易通过从更新前的职位中减去弹丸的当前职位，在每次更新时重新计算向前向量。为此，将以下函数放在你的弹丸类中。请记住，在绘制弹丸之前调用它，并将结果矩阵放入适当的变换矩阵中，遵循I.S.R.O.T顺序。此顺序指定了乘法变换矩阵的顺序，即Identiy Matrix、Scaling、Rotation、Orientation和Translation。

public Matrix ConstructOrientationMatrix(){
    Matrix orientation = new Matrix();

    // get orthogonal vectors dependent on the projectile's aim
    Vector3 forward = pos - prevPos;     
    Vector3 right = Vector3.Cross(new Vector3(0,1,0),forward);
    Vector3 up = Vector3.Cross(right,forward);

    // normalize vectors, put them into 4x4 matrix for further transforms
    orientation.Right = Vector3.Normalize(right);
    orientation.Up = Vector3.Normalize(up);
    orientation.Forward = Vector3.Normalize(forward);
    orientation.M44 = 1;  
    return orientation; 
}

线性飞行

显示速度为(5,3,2)的球的线性运动。

线性飞行是指沿着直线的运动。当球被直线快速抛出时，可能会观察到这种运动。显然，即使这样的球最终也会落到地面，除非在它停止之前被阻止。但是，如果例如在球离开投掷者的手后很快就被接住，那么它的弹道看起来是线性的。为了简化这种运动，加速度和重力被忽略，并且速度始终相同。运动方向由速度向量给出，与枪、手等的瞄准方向相同。

如果你的游戏中存在活动弹丸，那么XNA Update函数需要调用一个函数，该函数会为每个活动弹丸对象更新位置。弹丸的新位置是通过以下方式计算的
$pos=pos+velocity\times {timePassed}$，其中timePassed是自上次更新以来经过的时间。

此函数只需要一个参数，即自上次更新以来经过的游戏时间。Cawood 和 McGee 建议通过除以 90 来缩放此时间，因为否则每帧计算的位置将相距太远。

private void LinearFlight(GameTime timePassed){
    prevPos = pos; 
    pos = pos + velocity * ((float)timePassed.ElapsedGameTime.Milliseconds/90.0f);
}

拱形飞行

显示球的简化拱形弹道。

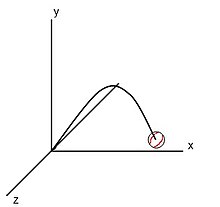
拱形弹道对于大多数飞行物体来说比线性飞行更真实，因为它考虑了重力。请记住，重力是一种加速度。为了计算具有恒定加速度的弹丸在特定时间点的位置，公式是
$pos={\frac {1}{2}}{a}{t}^{2}$，其中a是加速度，t是经过的时间。
由于重力将弹丸拉向地球，因此只有弹丸的y坐标会受到影响。弹丸的上升速度会随着时间的推移而降低，直到它停止上升并开始下降。但是，x坐标和z坐标不受此影响，它们与线性弹道的计算方式相同。以下公式显示了如何计算y坐标
${pos_{y}}=({pos_{y}}+{velocity_{y}}\times {timePassed})-{\frac {1}{2}}\times {gravity}\times {totalTimePassed}^{2}$
，其中totalTimePassed是自弹丸开始运动以来经过的时间。
被减数等于线性飞行公式，减数是由于重力导致的向下加速度。很明显，弹丸速度越低，速度方向越指向地面，重力就会越快获胜。此函数将更新弹丸的弹道。

private void ArchingFlight(GameTime timePassed){
    prevPos = pos; 
    // accumulate overall time
    totalTimePassed += (float)timePassed.ElapsedGameTime.Milliseconds/4096.0f ;
    
    // flight path where y-coordinate is additionally effected by gravity
    pos = pos + velocity * ((float)timePassed.ElapsedGameTime.Milliseconds/90.0f);
    pos.Y = pos.Y - 0.5f * GRAVITY * totalTimePassed * totalTimePassed;
}

我将添加到总时间的时间缩小了，这样重力就不会立即生效。对于速度为 1，按 4096 缩放会产生一个不错的飞行路径。另外，编译器希望能够进行合理的处理并优化除以 4096，因为它是 2 的倍数。你可能想尝试调整缩放因子。如果你的游戏不是在地球上设置的，你还应该考虑重力常数是否不同。

影响

一旦你的弹丸开始移动，你可能想进行一些碰撞检测，如果你希望它击中任何东西。有关如何进行碰撞检测的更多信息和详细信息，请查看关于碰撞检测的章节。如果检测到碰撞，就该考虑弹丸和被击中物体将会发生什么。撞击的效果高度依赖于你的弹丸是什么。球可以弹回，非常快的小子弹可能会穿透物体并继续移动，而另一方面，一个大的鱼雷可能会爆炸。在被击中物体的类中决定适当的反应更容易，并且可能播放指定的音效或动画。否则，你必须在弹丸类中跟踪弹丸对游戏中每个物体可能产生的所有效果。为了保持简单，只需在弹丸类中包含一些定义弹丸可能行为的函数，并在检测到碰撞时从被击中物体类中调用适当的函数。例如，当球击中地面时，它可能会简单地弹回。为了模拟这种行为，在弹丸类中使用以下函数，并在检测到球到达地面时调用它。它所做的只是反射入射方向并降低速度。当速度为零或更小时，球已停止移动，无需继续更新其飞行路径。'reflectionAxis' 向量仅包含 1，除了需要反转方向的轴，此值必须为 -1。

public void bounce(Vector3 incomingDirection, Vector3 reflectionAxis){
    //reflect the incoming projectile and normalize it so it's "just" a direction
    Vector3 direction = Vector3.Normalize(reflectionAxis* incomingDirection);
    speed -= 0.5f;                   // reduces the speed so the arche becomes lower
    velocity = speed * direction;    // the new velocity vector
    totalTimePassed= 0;                     // gravity starts all over again
    if (speed <= 0)bmoving= false;   // no speed no movement
}

当球应该从地面反弹回来时，对该函数的调用可能类似于以下代码，因此它的 y 方向需要反转。

ball.bounce(ball.position - ball.previousPosition, new Vector3(1, -1, 1));