普通天文学/运动和引力

普通天文学
观测天文学	运动和引力	光学原理

编辑章节

天文学的早期起源

几千年前，夜空比今天更贴近日常生活。没有来自路灯的光污染，任何人都可以看到数千颗星星，或者银河系穿过天空的路径。星星的运动为预测天气提供了一个重要的日历，因此古代人非常注意并观察天空和周围环境。这些古代的观测是现代天文学的基础，也是社会中科学思想的最初表现形式。

科学推理中的一个中心原则是，世界本质上是有序的，是可以理解的，观察是我们可以了解宇宙如何运作的方式。然而，没有什么需要宇宙有意义或可以被人理解。人类对科学方法背后的思想抱有信任，因为科学取得了如此巨大的成功，并且世界上有如此多的东西确实遵循一套规则。

构成成功科学哲学的要素不是一蹴而就的，而是在整个历史过程中逐渐发展而成的。古代人永远无法预先知道哪些科学方法原理最终会被证明是可靠的。在青春期，社会在黑暗中摸索，了解世界，发现他们的经验如何教会他们宇宙的样子，并确定理性与迷信之间的界限。世界各地文化中科学发展的故事不仅揭示了世界和真理的本质，而且也揭示了人类本质的一般特征。

可以追溯到 2 万年前旧石器时代的古代文物，可能与天文学有关，尽管对这些文物的解释是一个有争议的话题。最著名的例子是在法国拉斯科洞穴中发现的，那里有各种各样的旧石器时代艺术品。在洞穴中发现的一些标本可能描绘了昴宿星团或黄道带。附近的动物骨头有标记，表明它们可能被用作月球日历。尽管来自旧石器时代的文物稀少且模棱两可，但这并不一定意味着那个时代的人们对天空不感兴趣。例如，现代土著文化会流传下具有强烈天文象征意义的仪式，这些仪式不会反映在考古文物中。

新石器时代的文物特征明显不同，因为即使在最早的时代，对天空和日历的理解对于农业文化显然具有深刻的意义。观察者获得了管理重大年度事件计划的能力。天体的运动对人类事务产生了深远的影响，这种影响表现为对天体现象的宗教解释以及对行星的崇拜，这些实践形成了占星术和天文学起源。

古代纪念碑和标记向考古学家和历史学家展示了社会早期对天空的兴趣。这一时期许多坟墓都与基点一致。古代的纪念碑和祭坛都朝东、南或西，误差在几度之内——这清楚地表明，新石器时代的人们很早就开始识别天文学中最基本的概念。最著名的古代纪念碑是巨石阵。纪念碑的石头标志着夏至日日出的位置，等等。

自史前时代以来，人们就已知几颗行星。这些天体非常明亮，它们在固定恒星之间游荡，穿过星座。希腊人称它们为planētēs，意思是“游荡者”。古代人知道 7 颗“行星”：太阳、月亮、水星、金星、火星、木星和土星。一周七天的名称来自北欧神：星期日（太阳），星期一（月亮），星期二（火星/Tiw），星期三（水星/Wodan），星期四（木星/Thor），星期五（金星/Frigg），星期六（土星/Soeternes）。

早在公元前 3 千年，在巴比伦的古代美索不达米亚文明中，就出现了高度系统化且经过仔细记录的天空观测。巴比伦人还开发了最早的计时工具。然而，也许更重要的是，占星术在美索不达米亚诞生。巴比伦的占星家是第一个假设天体事件和地球事件之间存在因果关系的人，也是第一个想象自然界中存在潜在秩序的人——尽管人类和天体事件之间没有真正的联系，但占星术的预言是现代科学预言的祖先。

早期的天文学家对他们周围的世界了解很多。到了亚里士多德时期，许多人认为世界是圆的。他们从几个证据来源了解到这一点。

当船只驶出地平线时，从陆地观望的人会先看到船体消失，然后看到船帆消失。水手看到陆地从底部开始沉入地平线。从这一点，他们得出结论，世界的表面是弯曲的，船正在绕着地球的曲率移动。
古代人认为月食是地球的阴影。在月食期间看到的阴影总是圆形的。唯一总是投射圆形阴影的形状是球体。这表明地球是球形的。
旅行者注意到，当他们在旅途中移动时，新的星星变得可见。当旅行者向北移动时，北极星和北天星座在天空中获得高度。古代人认识到，这意味着地球是弯曲的。

亚里士多德在他的著作中提到，他那个时代的一些思想家认为地球是平的，而另一些人则认为地球是球形的。他自己坚定地认为地球是一个球体。在亚里士多德之后，几乎所有西方作家都声称地球是一个球体。

埃拉托色尼知道，在塞恩城，方尖碑在夏至日的中午不会投射阴影。然而，在亚历山大，方尖碑投射阴影。这揭示了地球不是平的，并且可以测量其周长。

在公元前 3 世纪，希腊埃及学者埃拉托色尼担任亚历山大图书馆馆长，在那里他对各种学科进行研究和写作。在他的研究过程中，埃拉托色尼得知太阳在夏至日的中午不会在塞恩城投射阴影。从亚历山大，埃拉托色尼观察到太阳确实投射了阴影，他测量到当太阳位于天空最高点时，太阳和天顶之间的角度约为 7 度。

埃拉托色尼知道，如果假设太阳在同一时间在两个城市都处于最高点，他可以通过测量亚历山大和塞恩之间的距离来测量地球的周长。由于 7 度是圆周的 7/360，因此塞恩和亚历山大之间的距离必须是地球周长的 7/360（或相当于约 1/50）。

埃拉托色尼估计塞恩和亚历山大之间的距离约为 5,000 斯塔迪亚，并得出结论，地球的周长约为 50 倍，即 250,000 斯塔迪亚。斯塔迪亚是古代世界常用的距离单位，与现代使用的公里或英里相当；斯塔迪亚的确切长度在历史上和各个地区有所不同，因此很难将埃拉托色尼的估计值与现代值进行比较。然而，大多数斯塔迪亚的值都转化为大约 40,000 公里的周长，这与公认的 40,070 公里的周长非常接近。

随着科学开始在西方文明的文化中发展，它也在世界其他地方扎根。古代和中世纪的中国、印度和美洲，特别是科学世界的中心。

印度的科学史是世界上最长、记录最完整的科学史之一。在早期历史上长期与世界其他地区隔绝，印度可以自由地以自己的节奏发展其独特的观测天文学风格，不受外部影响。古代印度没有占星术体系，但天体计时法很早就流行起来。第一批天文学家监测了一年的进程，并追踪太阳、月亮和行星在nakshatra（印度黄道）中的运动。

这些观测的质量使得后来的印度天文学家能够像喜帕恰斯对希腊天文学所做的那样，探测到岁差的影响。中世纪的印度天文学家估计岁差速度为每年 54 秒。尽管这比喜帕恰斯的测量结果要准确得多，但我们必须注意，数字 54 是出于神秘原因而不是科学原因选择的。世界各地的古代人以这种方式将神秘主义与算术混合在一起，但在印度文化中，这种现象比任何其他文化都更加一致。

基督教纪元的到来给印度天文学带来了巨大的变化。大约公元 519 年，巴比伦的征服已经蔓延到印度河盆地，许多希腊学者也已经访问或定居在那里。自然而然地，文化交流开始扎根。

古代中国人非常重视天文学。对天体的系统性观测可能早在公元前 3 千年就开始了。科学被视为一种强大的工具，因此受到国家的严格保护。在王朝统治下，占星学和天文学的感知目的在于提醒人们皇帝与天体事件之间的联系。因此，占星学被专门分配给皇帝任命的“天文局”，并根据严格的规则执行。

中国人将天体事件视为重要的预兆，特别是在“客星”的情况下，客星是指暂时出现在天空中并迅速消失的恒星。如今我们知道，这些是称为超新星的恒星爆炸。公元 1054 年，一颗新的超新星变得足够明亮，即使在白天也能看到。中国和阿拉伯天文学家记录了这一事件，它似乎被描绘在美国的一个洞穴壁画中。由于中国人重视超新星，他们对古代超新星的观测是世界上迄今为止最完整的，并且即使在今天也仍然是科学数据的宝贵来源。

与此同时，天文学在哥伦布前的美洲蓬勃发展，人们对天体的兴趣很普遍。天文学在玛雅文明中占有重要地位，玛雅文明在欧洲人到来之前统治中美洲长达 2000 年。玛雅人认为，自然界的模式非常重要，并且应该可以使用占星学来预测未来，以此为基础。这使得观测天体周期变得非常重要，因为它们可以提前了解未来的事件，而玛雅人则忠实地跟踪太阳和月亮的运动。随着几个世纪的观测积累，玛雅天文学家能够很好地预测日食并测量天体周期的长度。

类似的想法在整个美洲大陆蔓延开来。在整个美洲大陆，古代人建造了与重要恒星的升起和落下点或月亮的最北端和最南端位置一致的纪念碑、建筑物、土堆和寺庙。像巨石阵这样的日历和纪念碑在这里也能找到。很明显，对天体的兴趣在整个古代世界都很普遍，科学的初步萌芽也是如此。

科学思想贯穿历史，遍布世界各地，但很明显，科学事业在某些地区和时期比其他地区和时期更加成功。造成这种情况的原因尚不清楚。文化、经济和哲学的哪些因素影响了科学思想的兴起？例如，巴比伦文化不允许任何偏离传统或常规做法。人们可能会期望这种文化阻碍科学的进步，但科学和数学在那里蓬勃发展。在古代中国，只有贵族才能从事科学研究。一些历史学家认为，这种文化阻止了中国在欧洲文艺复兴之前很久可能发生的文艺复兴。科学与社会学之间相互作用的问题一直是科学史研究中的一个重要课题。

虽然魔法和迷信是早期思想的重要组成部分，并且难以与新兴的科学追求区分开来，但说精神主义完全渗透了关于宇宙本质的最初想法是不公平的。科学精神，通过观察宇宙来了解宇宙的原则，即使在最早的时期也明显存在，而且科学思想已经非常普遍。阿那克西曼德（公元前 611-547 年）假设存在五种元素：土、气、火、水……以及构成天体的“以太”。

占星学的基础是托勒密于公元 140 年撰写的《四书》。黄道被分为 12 个“宫位”，黄道上的 12 个星座。托勒密认为，一个“第八球”支撑着天空中的恒星。

动能是运动的能量。它的公式是 ${\frac {1}{2}}MV^{2}$ ( $M$ 是质量，而 $V$ 是速度)。在 16 世纪中叶日心模型被普遍接受之前，地球被认为是已知宇宙的中心。地心宇宙模型中许多固有的问题导致尼古拉·哥白尼提出了行星和恒星运动的另一种方式。这两个问题是：一些行星（特别是火星）的视逆行运动，以及为了弥补这个问题而产生的本轮理论，以及发生的维纳斯相位。

行星运动和本轮

将地球视为我们宇宙的中心，我们太阳系中的许多行星在夜空中呈现出奇特的运动。例如，火星似乎有时会逆行。由于地心模型认为我们太阳系中的所有行星都围绕地球运行，这意味着火星有时会改变其轨道方向，然后继续运行。希腊天文学家托勒密试图用本轮来解释这种现象——即行星围绕地球运行时，在它们围绕地球的圆形轨道上所遵循的小圆形运动。从希腊时代到启蒙运动的天文学家通过添加额外的本轮层来弥补地心模型中的缺陷，直到该系统变得如此复杂，以至于几乎无法使用。哥白尼的日心模型将太阳置于中心，行星围绕它运行，而不是围绕地球运行，消除了当时困扰天文学的许多本轮。

维纳斯相位

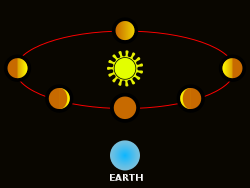
地心模型的另一个问题出现在观察金星及其相对相位时：如果金星和太阳都绕地球运行，那么金星不可能处于“满月”相位，也就是说完全被照亮（类似于满月）。因此，托勒密模型只预测了金星的月牙形和新月形相位。然而，正如伽利略所观察到的，情况显然并非如此；金星表现出月亮的所有相位，这是哥白尼模型预测和解释的一种现象。伽利略发现了这种现象，这是最终支持日心宇宙观的关键因素之一。

请注意，这只是伽利略做出的许多与古代信仰相矛盾的观察结果之一，但这一个最直接地对行星绕地球运行的想法提出了质疑。

参考文献

Shea, William R. 伽利略在罗马：一个麻烦天才的兴衰。纽约：牛津大学出版社，美国，2004 年。

现代日心宇宙模型是由尼古拉·哥白尼在他的《天体运行论》一书中提出的，该书在他去世前出版，以避免因异端罪被起诉。它解决了与托勒密模型相关的许多问题，托勒密模型需要大量的本轮来描述行星运动。日心说将太阳置于太阳系的中心。虽然印度和中东的一些古代文明曾在之前提出过日心模型，但哥白尼的发现为现代太阳系观奠定了基础。

哥白尼模型

在哥白尼的日心模型中，他提出了七个理论。

宇宙中存在不止一个中心。
宇宙的中心位于太阳附近。
地球不是我们宇宙的中心。
地球与太阳之间的距离尺度与地球与天空中的恒星之间的天文距离相比是微不足道的。
地球绕太阳公转，因此造成了我们所见到的季节的年度循环。
地球的自转导致恒星看起来每晚都在移动，而不是恒星本身的任何运动。
任何逆行运动，以前用本轮解释，实际上是由行星围绕太阳的轨道速度不同造成的。

哥白尼多年来一直怀有他对日心说的信仰，直到 1542 年，在他去世前一年，才发表了他的著作。有些人推测哥白尼在相当长的时间里坚持自己的想法，仅仅是因为他害怕它在同行中会受到怎样的评价，更重要的是，它会受到教会的怎样的评价。许多人认为《天体运行论》(On the Revolution of the Celestial Sphere) 的出版标志着科学革命的开始。

在随后的几年里，哥白尼的理论得到了著名的科学家的完善和独立验证，其中最突出的是伽利略和开普勒。具体来说，伽利略注意到金星的所有相位都出现了（类似于我们的月亮），这在以地球为中心的模型中无法得到充分解释。这与地心模型预测的只有新月和弦月相矛盾。

教会的接受

火箭背后的原理是在公元前 100 年发现的。早期的火箭是汽转球，一种蒸汽动力装置。约翰内斯·开普勒是一位数学家，他试图推导出一个基本原理集，以解释行星的运动。他相信哥白尼提出的日心说，并且他也拥有第谷·布拉赫对行星的大量观测数据。

经过二十年的艰苦尝试和基于几何学的各种被抛弃的想法，他终于得出了一个基于椭圆的轨道运动数学模型。开普勒将他的发现总结为行星运动的三定律，通常被称为开普勒第一定律、第二定律和第三定律。

开普勒第一定律，也称为椭圆定律——行星的轨道是椭圆，太阳位于一个焦点上。
开普勒第二定律，或等时间等面积定律——行星与太阳之间的直线在行星轨道平面上扫过相等的时间间隔内的相等面积。
开普勒第三定律，或和谐定律——行星绕太阳运行所需的时间，称为周期，与其椭圆长轴的一半的 3/2 次方成正比。比例常数对于所有行星都是相同的。它通常被称为和谐定律，因为它显示了距离和周期之间的和谐关系。

在他制定这些定律的时候，还没有发展出能够解释行星运动的原因的引力理论。后来，艾萨克·牛顿利用他提出的万有引力平方反比定律，证明了开普勒定律是如何融入天体力学科学理论的。

椭圆轨道

椭圆是通过对圆锥体进行对角切片形成的形状。它本质上是一个圆的形状，只是从一个角度观察。

可以取一张纸、两根大头针、一根绳圈和一支铅笔来画椭圆。将两根大头针穿过纸张插入合适的表面，为椭圆提供两个焦点。它们应该比绳圈长距离更靠近在一起。将绳圈放在这些大头针的底部周围，留出一些松弛。现在将铅笔放置好，使大头针和绳圈形成一个三角形，绳子略有张力。

现在尝试在保持绳子绷紧的情况下，围绕着大头针移动铅笔来绘制一个形状。结果应该是一个椭圆。可以通过将大头针移动到更靠近在一起或更远离在一起来改变椭圆的形状。开普勒认为，这种形状定义了行星围绕太阳运行时的轨迹。

开普勒第一定律——行星围绕太阳运行的轨道是一个椭圆，太阳位于一个焦点上。

简而言之，开普勒第二定律说，物体越靠近太阳，速度就越快，越远离太阳，速度就越慢。在从太阳到轨道路径的距离更长的地方，只需要遍历更小的弧线就可以扫过一个需要在太阳附近遍历更宽弧线的区域。

当行星沿其轨道靠近太阳时，引力作用使速度增加。相反，当行星远离太阳时，太阳的引力逐渐减速，行星的速度也随之减慢。

开普勒第二定律——轨道上的行星围绕太阳扫过相等面积

A

在相同的时间间隔内

t

.

将椭圆分成两半并穿过椭圆最宽部分的直线称为长轴。垂直于此轴并将椭圆分成两半的直线称为短轴。长轴的一半称为半长轴，用 $a$ 表示。行星完成一个完整轨道所需的时间用 $P$ 表示。周期P 与半长轴长度 $a$ 之间的关系被称为开普勒第三定律，可以表示如下

P^{2}\propto a^{3}

其中符号 ∝ 表示“与...成正比”，意味着周期平方与半长轴立方之间存在直接的数学关系。

第二定律和第三定律为计算围绕太阳运行的任何行星的周期以及确定行星在轨道路径上的位置提供了基础。

偏心率和轨道路径

椭圆的焦点到中心距离与半长轴的比值称为轨道的偏心率。当椭圆的两个焦点重叠时，偏心率恰好为 0.0，形状为圆形。随着偏心率的增加，轨道行星的距离比最靠近时更远。我们太阳系中行星的轨道偏心率从水星的 0.21 到金星的 0.0068 不等。

最靠近点的科学名称是近拱点，而最远距离是远拱点。在行星绕太阳运行的情况下，它们分别被称为近日点和远日点。（-helion 后缀来自太阳神 Helios 的希腊名字。这个词也是元素氦的名称来源。）

两个具有相同长轴

a

但偏心率不同的椭圆轨道。

也许第三定律最反直觉的一方面是，对于围绕太阳运行的两个相同的物体，如果它们具有相同的半长轴，则轨道周期相同。即使一个是完美的圆形轨道，另一个是高度椭圆的轨道（具有相对较高的偏心率），情况也是如此。除了两点（长轴的末端，两条曲线将在那里相切）之外，椭圆形将完全适合圆形，因此它实际上是一个更短的轨道路径。但是，椭圆的远日点将位于距离太阳更远的地方，因此行星将花费更多的时间来遍历轨道的远端部分。更短的轨道和更慢的远日点遍历相互抵消，导致与圆形轨道相同的周期。

使用开普勒第三定律的一些例子

最初，开普勒第三定律被用来描述行星围绕太阳的运动。事实证明，它也适用于其他二体轨道系统，例如卫星绕木星运行的轨道或双星绕其系统质心运行的轨道。在所有这些情况下，轨道的周期平方都与半长轴立方成正比，轨道系统之间的差异反映在比例常数中。

在本节中，我们将考虑行星绕太阳运行的特殊情况。如果我们选择以天文单位（AU）为单位来测量轨道半长轴的长度（1 AU 为地球到太阳的距离），并且以年（缩写为 $y$ ）为单位来测量轨道周期，那么我们可以将开普勒第三定律表示为

P^{2}=\left({\frac {y^{2}}{AU^{3}}}\right)a^{3}

其中 $P$ 以年为单位， $a$ 以天文单位为单位。以下是使用此方程的一些示例。

火星的轨道周期

多次测量火星的轨道表明，其轨道半长轴的长度为 1.52 AU。火星绕太阳运行一周需要多长时间？

解决方案：在这个问题中，我们要问的是火星的轨道周期 $P$ 。从问题中我们可以知道轨道半长轴的长度 $a$ 为 1.52 AU。根据开普勒第三定律求解周期，得到

P=\left({\frac {y}{\sqrt {AU^{3}}}}\right){\sqrt {a^{3}}}=\left({\frac {y}{\sqrt {AU^{3}}}}\right){\sqrt {(1.52AU)^{3}}}=1.87y

这告诉我们火星绕太阳运行一周需要 1.87 年。

一颗未知小行星的轨道半长轴

一位业余天文学家花了几个月时间跟踪一颗小行星，并确定它绕太阳运行一周大约需要 3/4 年。这颗小行星轨道的半长轴是多少？

解决方案：从问题中我们可以知道小行星的轨道周期是 3/4 年，也就是 0.75 $y$ 。我们需要找到轨道半长轴的长度 $a$ ，因此我们需要根据开普勒第三定律求解。这样一来，我们得到

a=\left({\frac {AU}{\sqrt[{3}]{y^{2}}}}\right){\sqrt[{3}]{P^{2}}}=\left({\frac {AU}{\sqrt[{3}]{y^{2}}}}\right){\sqrt[{3}]{(0.75y)^{2}}}=0.83AU

这意味着它的半长轴位于金星轨道和地球轨道之间。

普通天文学
观测天文学	运动和引力	光学原理