普通力学/扭矩和角动量

普通力学

扭矩

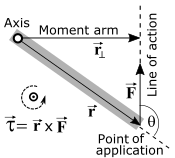
扭矩是作用于一个质量上的力，使它绕一个点（称为原点）旋转。它被定义为

{\vec {\tau }}={\vec {r}}\times {\vec {F}}

其中 $r$ 是质量相对于原点的位移。

需要注意的是，在许多情况下扭矩为 0。如果力的方向直接指向或远离原点，叉积为零，导致扭矩为零，即使力不为零。同样地，如果 $r=0$ ，扭矩为 0。因此，作用于原点的力不会产生扭矩。这两个极限直观上是有道理的，因为它们都没有使质量绕原点旋转。

质量相对于点 O 的角动量定义为

{\vec {L}}={\vec {r}}\times {\vec {p}}

其中 p 是质量的普通（也称为“线性”）动量。如果物体的运动直接指向或远离原点，或者它位于原点，则角动量为 0。

如果我们取位置矢量和牛顿第二定律的叉积，我们会得到一个将扭矩和角动量联系起来的方程

{\vec {r}}\times {\vec {F}}={\vec {r}}\times {\frac {d{\vec {p}}}{dt}}={\frac {d}{dt}}({\vec {r}}\times {\vec {p}})-{\frac {d{\vec {r}}}{dt}}\times {\vec {p}}

由于平行矢量的叉积为零，这简化为

{\vec {\tau }}={\frac {d{\vec {L}}}{dt}}

这是牛顿第二定律的旋转版本。

对于扭矩和角动量，原点的位置是任意的，通常选择最方便的位置。但是，必须为扭矩和角动量选择相同的原点。

对于中心力的情况，即沿着两个物体之间的中心线作用的力（如重力），通常存在一个特别方便的原点选择。如果原点放在太阳的中心（假设它不会受到行星引力的影响而移动），那么太阳的引力对行星施加的扭矩为 0，这意味着行星绕太阳中心的角动量是恒定的。其他任何原点选择都不会产生这种方便的结果。

我们已经了解了两个基本的守恒定律——能量和线性动量的守恒定律。我们相信角动量在孤立系统中也是守恒的。换句话说，粒子可以在彼此之间交换角动量，但是孤立于外部影响的所有粒子的角动量的矢量和必须保持恒定。

在现代观点中，角动量守恒是空间各向同性性的结果——即空间的特性不依赖于方向。这与普通动量守恒是空间齐次性的结果完全类似。我们记得，普通动量守恒是空间齐次性的结果。

如果一个物体绕着一个轴旋转， $n$ 是单位向量，以频率 $\omega$ 旋转，我们说它具有角速度 ${\vec {\omega }}$ 。尽管名称如此，但这 *并非* 角度变化率，甚至不是向量变化率。

如果一个常数向量 ${\vec {r}}$ 以角速度 ${\vec {\omega }}$ 绕固定点旋转，则

{\frac {d{\vec {r}}}{dt}}={\vec {\omega }}\times {\vec {r}}

这意味着加速度始终垂直于速度和旋转轴。

当轴发生变化时， ${\vec {\omega }}$ 可以定义为使得此关系成立的向量。

注意，在这个等式左侧， ${\vec {r}}$ 是固定坐标系中的向量，具有可变分量，而在等式右侧，其分量是在运动坐标系中给出的，在那里它们是固定的。

我们可以使用下标来更清楚地区分它们， $r$ 表示旋转的， $f$ 表示固定的，然后将此扩展到任意向量

{\frac {d{\vec {g}}_{f}}{dt}}={\frac {d{\vec {g}}_{r}}{dt}}+{\vec {\omega }}\times {\vec {g}}_{f}

对于 *任何* 向量 ${\vec {g}}$

利用这个，我们可以写出旋转系中的牛顿第二定律。

{\begin{aligned}{\vec {F}}_{f}&=m{\dfrac {d{\vec {v}}_{f}}{dt}}\\&=m{\dfrac {d{\vec {v}}_{r}}{dt}}+m{\vec {\omega }}\times {\vec {v}}_{f}\\&=m{\ddot {\mathbf {r} }}_{r}+m{\boldsymbol {\omega }}\times \left(2{\dfrac {d_{2}{\vec {r}}_{r}}{dt_{2}}}+{\vec {\omega }}\times {\vec {r}}_{f}\right)\end{aligned}}

或者，重新排列

m{\vec {a}}_{r}={\vec {F}}-2m({\vec {\omega }}\times {\vec {v}}_{r})-m{\vec {\omega }}\times ({\vec {\omega }}\times {\vec {r}})

质量的行为就好像有两个额外的力作用于它。第一项， ${\vec {\omega }}\times {\vec {v}}$ 被称为*科里奥利*力。第二项是熟悉的离心力。