直角坐标系,也称为笛卡尔坐标系,是一种系统化的定位物体的方法。它是由一位名为笛卡尔的数学家发明的。它与地理或计算机素养中的坐标系相似,但并不完全相同。
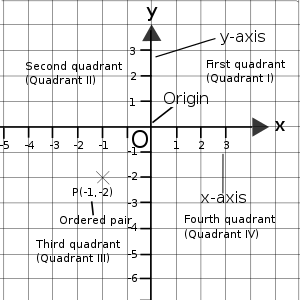
笛卡尔平面相关基本术语的总结 直角坐标平面,或称为笛卡尔平面,由两条轴组成,即x轴和y轴。x轴是水平轴,而y轴是垂直轴。这两条轴的交点称为原点,始终命名为O 。x轴和y轴上是刻度,这与统计图表中的刻度非常相似,只是这里有负数。事实上,它们看起来像数轴,一条水平,一条垂直,‘0’点重叠。
我们可以使用有序对在坐标系中定位一个点。有序对由两个数字组成:两条轴的读数。我们先写x轴的读数,然后写y轴的读数,像这样:(x, y)。坐标平面被分成四个部分:第一象限(象限I)、第二象限(象限II)、第三象限(象限III)和第四象限(象限IV)。四个象限的位置可以在右边的图中找到。一个点可以位于这四个象限中的任何一个,也可以位于x轴、y轴或原点。我们可以仅通过查看点的坐标来找出有序对的一些基本属性。
象限I: (x , y )
象限II: (-x , y )
象限III: (-x , -y )
象限IV: (x , -y )
x轴: (x 或 -x , 0)
y轴: (0, y 或 -y )
原点: (0, 0) 确定一个点的有序对时,请记住刻度不一定是一对一的。这意味着数字不必是0, 1, 2, 3, 4。它们也可以是0, 2, 4, 6, 8,甚至5, 10, 15, 20。
如果您完全确定两点形成一条水平线或垂直线,水平线的定义是平行于x轴,垂直线的定义是平行于y轴,那么您可以参考另一个点,而无需刻度的帮助来找到一个或两个点的坐标。例如,如果P (3, 4) 与Q (3, y ) 位于同一条垂直线上,那么y = 4。
我们将用一个复杂的问题来介绍下一部分(见右边的图)。
求
QP 的长度所有阴影区域的面积之和
如果F :(-2, -3),那么I 的坐标 乍一看有点复杂,所以让我们从第一象限上的直线QP 开始,这条直线看起来相当容易。如果可以的话,我们将计算出所有未知数,并解决第一个目标。首先,让我们看看P 的坐标。它们是(1, 2)。由于P 和Q 位于同一条水平线上,所以它们的y 坐标必须相同。因此,Q 的坐标必须是(3, 2)。换句话说,z = 2。要找到PQ的长度,我们只需找到它们的x 坐标之差即可;在本例中,3 - 1 = 2 个单位。因此,QP = 2 个单位。在数学表达中,应该是
∵ The y -coordinate of P = 2 ∴ z = 2 {\displaystyle {\begin{aligned}\because {\text{The }}y{\text{-coordinate of }}P=2\\\therefore z=2\end{aligned}}}
The length of P Q = 3 − 1 = 2 units {\displaystyle {\begin{aligned}{\text{The length of }}\ PQ&=3-1\\&=2{\text{ units}}\end{aligned}}}
太好了!现在我们已经解决了第一个目标,让我们继续研究第二象限上的小三角形。同样,我们将计算出所有未知数。首先,让我们看看C 的x 坐标。我们已经知道z = 2,所以-z 必须是 -2,C 的x 坐标也是如此。y 坐标呢?我们知道B和C位于同一条水平线上,所以它们的y 坐标必须相同。因此,C 的y 坐标也必须是1,并且y = 1。B 的x 坐标,称为x ,也是缺失的。由于A和B位于同一条垂直线上,所以它们的x 坐标必须相同。因此,我们可以推断x = -4。在数学表达式中
The x -coordinate of C = − z = 1 {\displaystyle {\begin{aligned}{\text{The }}\ x{\text{-coordinate of }}\ C&=-z\\&=1\end{aligned}}}
∵ The y -coordinate of B = 1 ∴ y = 1 {\displaystyle {\begin{aligned}\because {\text{The }}y{\text{-coordinate of }}B=1\\\therefore y=1\end{aligned}}}
∵ The x -coordinate of A = − 4 ∴ x = − 4 {\displaystyle {\begin{aligned}\because {\text{The }}x{\text{-coordinate of }}A=-4\\\therefore x=-4\end{aligned}}}
接下来,我们将求出三角形 ABC 的面积。这在求阴影区域的总面积时将非常有用。在计算之前,我们必须先求出三角形的底和高。你还记得三角形面积公式吗?它是底乘以高除以二。让我们选择 BC 作为三角形的底。由于 AB 和 BC 互相垂直,AB 可以作为高。由于 BC 是水平线,BC 的长度就是 B 和 C 的 x 坐标之差。即 -4 和 -1,所以 BC 的长度为 [(-1)-(-4)] 单位 = 3 单位。对于 AB,情况则相反。由于 AB 是垂直线,我们应该找到它们的 y 坐标之差。在本例中,即为 (3-1) 单位 = 2 单位。因此,三角形 ABC 的面积为 (3-2) 平方单位 = 1 平方单位。让我们用数学表达式来表示。
The length of B C = x − ( − z ) units = [ ( − 1 ) − ( − 4 ) ] units = 3 units {\displaystyle {\begin{aligned}{\text{The length of }}\ BC&=x-(-z){\text{ units}}\\&=[(-1)-(-4)]{\text{ units}}\\&=3{\text{ units}}\end{aligned}}}
The length of A B = 3 − 1 units = 2 units {\displaystyle {\begin{aligned}{\text{The length of }}\ AB&=3-1{\text{ units}}\\&=2{\text{ units}}\end{aligned}}}
The area of △ A B C = B C × A B 2 sq. units = 3 × 2 2 sq. units = 3 units {\displaystyle {\begin{aligned}{\text{The area of }}\ \triangle ABC&={\frac {BC\times AB}{2}}{\text{ sq. units}}\\&={\frac {3\times 2}{2}}{\text{ sq. units}}\\&=3{\text{ units}}\end{aligned}}}
现在我们只需要计算出两个下象限图形的面积。该图形的形状类似于梯形,旁边粘着一个三角形,中间有一个洞。利用我们之前学到的知识,你应该可以算出 a = -4 且 b = -6。注意,我们已经知道上面 -z 的值,即 -2。现在我们要找到梯形、三角形和正方形孔的面积。让我们先计算三角形的面积。从 Z 点画一条与 XY 垂直的虚线,并命名为 R。参考 X 和 Z 点,R 点的坐标为 (-4, -5)。ZR 和 XY 的长度应分别为 1 和 4,因此三角形 XYZ 的面积一定是 2 平方单位。具体细节如下面的数学表达式所示。
∵ The x -coordinate of X = − 4 ∴ a = − 4 {\displaystyle {\begin{aligned}\because {\text{The }}x{\text{-coordinate of }}X=-4\\\therefore a=-4\end{aligned}}}
∵ The y -coordinate of Y = − 6 ∴ b = − 6 {\displaystyle {\begin{aligned}\because {\text{The }}y{\text{-coordinate of }}Y=-6\\\therefore b=-6\end{aligned}}}
The y -coordinate of D = − z = − 2 {\displaystyle {\begin{aligned}{\text{The }}y{\text{-coordinate of }}D=-z\\=-2\end{aligned}}}
The length of Z R = ( − 5 ) − ( − 4 ) units = 1 units {\displaystyle {\begin{aligned}{\text{The length of }}\ ZR&=(-5)-(-4){\text{ units}}\\&=1{\text{ units}}\end{aligned}}}
线段 X Y = ( − 2 ) − ( − 6 ) 个单位 = 4 个单位 {\displaystyle {\begin{aligned}{\text{The length of }}\ XY&=(-2)-(-6){\text{ units}}\\&=4{\text{ units}}\end{aligned}}}
三角形 △ X Y Z = Z R × X Y 2 平方单位 = 1 × 4 2 平方单位 = 2 平方单位 {\displaystyle {\begin{aligned}{\text{The area of }}\ \triangle XYZ&={\frac {ZR\times XY}{2}}{\text{ sq. units}}\\&={\frac {1\times 4}{2}}{\text{ sq. units}}\\&=2{\text{ sq. units}}\end{aligned}}}
现在我们要找到直角梯形的面积。你还记得梯形的面积公式吗?它是平行边之和乘以高除以二。我们需要找到平行边的长度和高度才能求出面积。我们已经知道高度 *XY*。线段 *XD* 和 *YE* 的长度分别为 9 和 8,所以梯形的面积为 34 平方单位。具体细节如下。
线段 X D = ( − 4 ) − 5 个单位 = 9 个单位 {\displaystyle {\begin{aligned}{\text{The length of }}\ XD&=(-4)-5{\text{ units}}\\&=9{\text{ units}}\end{aligned}}}
线段 Y E = ( − 4 ) − 4 个单位 = 4 个单位 {\displaystyle {\begin{aligned}{\text{The length of }}\ YE&=(-4)-4{\text{ units}}\\&=4{\text{ units}}\end{aligned}}}
梯形 X Y D E = ( X D + Y E ) × X Y 2 平方单位 = ( 9 + 4 ) × 4 2 平方单位 = 26 平方单位 {\displaystyle {\begin{aligned}{\text{The area of trapezium}}\ XYDE&={\frac {(XD+YE)\times XY}{2}}{\text{ sq. units}}\\&={\frac {(9+4)\times 4}{2}}{\text{ sq. units}}\\&=26{\text{ sq. units}}\end{aligned}}}
我们的下一步是找到正方形的面积。正方形的面积公式是边长的平方,所以正方形 *FGHI* 的面积是 *z*2 = 22 单位 = 4 单位。
正方形 F G H I = F I 2 平方单位 = z 2 平方单位 = 2 2 平方单位 = 4 平方单位 {\displaystyle {\begin{aligned}{\text{The area of square}}\ FGHI&=FI^{2}{\text{ sq. units}}\\&=z^{2}{\text{ sq. units}}\\&=2^{2}{\text{ sq. units}}\\&=4{\text{ sq. units}}\end{aligned}}}
第二点的最后部分是使用我们从前面章节中学到的平面图形等技能,计算出阴影区域的总面积。第三和第四象限的阴影区域 = 五边形 XZYED 的面积 - 正方形 FGHI 的面积 = 三角形 XYZ 的面积 + 梯形 XYDE 的面积 - 正方形 FGHI 的面积 = (2+26-4) 平方单位 = 24 平方单位。然后我们将它加到三角形 ABC 的面积,得到 (24+3) 平方单位 = 27 平方单位。数学表达式如下所示。
The shaded area in quadrants III and IV = Area of △ X Y Z sq. units + Area of trapezium X Z Y E D − Area of square F G H I = ( 2 + 26 − 4 ) sq. units = 24 sq. units {\displaystyle {\begin{aligned}&{\text{The shaded area in quadrants III and IV }}\\&={\text{Area of }}\triangle XYZ{\text{ sq. units}}+{\text{Area of trapezium }}XZYED-{\text{Area of square }}FGHI\\&=(2+26-4){\text{ sq. units}}\\&=24{\text{ sq. units}}\end{aligned}}}
The sum of all shaded areas = ( 24 + 3 ) sq. units = 27 sq. units {\displaystyle {\begin{aligned}{\text{The sum of all shaded areas }}&=(24+3){\text{ sq. units}}\\&=27{\text{ sq. units}}\end{aligned}}}
既然我们已经完成了两个目标,现在该寻找第三个目标了。第三个目标需要一种与前面我们使用的方法相反的技术。你可能已经注意到,第三个目标与其他目标不同,它要求找到坐标,而不是测量值。请记住,我们从问题中知道的唯一坐标是点 *F* 的坐标。还要记住,正方形的四条边都相等。既然我们可以根据线段端点的坐标找到线段的长度,那么我们也可以根据线段的长度找到端点的坐标。
那么,我们究竟是如何做到的呢?*F* 的坐标是 (-2, -3)。我们可以找到 *I* 的 *y* 坐标,我们已经知道它与 *F* 的 *y* 坐标相同。因此,*y* 坐标为 -3。但是 *x* 坐标呢?既然我们知道 *FI* = *z* = 2 个单位,我们可以算出 *I* 的 *x* 坐标为 [(-2)+2)] 个单位 = 4 个单位。请记住,我们正在寻找的端点的坐标相对于我们已经知道的端点的坐标的位置是重要的。如果 *I* 在 *F* 的右边,而不是左边,它的 *x* 坐标将为 [(-2)-2)] 个单位 = -4 个单位。如果 *I* 在 *F* 的上方或下方,它们的 *x* 坐标将相同,而 *I* 的 *y* 坐标将为 [(-3)-2)] 个单位 = -5 个单位(下方)或 [(-3)+2)] 个单位 = -1 个单位(上方)。
∵ The y -coordinate of F = − 3 ∴ The y -coordinate of I = − 3 {\displaystyle {\begin{aligned}\because {\text{The }}y{\text{-coordinate of }}F=-3\\\therefore {\text{The }}y{\text{-coordinate of }}I=-3\end{aligned}}}
∵ F I = z = 2 units {\displaystyle {\begin{aligned}\because FI=z\\=2{\text{ units}}\end{aligned}}} ∴ The x -coordinate of I = [ ( − 2 ) + 2 ) ] = 4 {\displaystyle {\begin{aligned}\therefore {\text{The }}x{\text{-coordinate of }}I=[(-2)+2)]\\&=4\end{aligned}}}
就是这样!我们不仅学习了如何在直角坐标系中计算图形的长度和面积以及点的坐标,而且还看到了一个重要的例子,说明了面积是如何计算的。







![{\displaystyle {\begin{aligned}{\text{The length of }}\ BC&=x-(-z){\text{ units}}\\&=[(-1)-(-4)]{\text{ units}}\\&=3{\text{ units}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ed707e08315fbae43e73fe3df868022c03d38b7)
















![{\displaystyle {\begin{aligned}\therefore {\text{The }}x{\text{-coordinate of }}I=[(-2)+2)]\\&=4\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a56cf9a7a5b74462fa93f938d0c4c785f52b777f)