高中化学/使用数据

之前，我们学习了定性和定量观察，以及定量观察需要测量。在科学中，测量意味着数据。在接下来的部分中，我们将深入研究数据，以查看模式并绘制数据图表。有时我们可以绘制数据图表，进行计算，绘制直线并计算斜率。所有这些定量观察有助于我们形成基于证据的结论。

识别数据中的模式

如前所述，数据可以为科学家提供大量信息，以进行解释和得出结论。为了做到这一点，科学家必须能够查看一组数据并识别模式。数据可以以图片、图表或图形的形式存在。例如，在（图 3.1）中找到的图片。尽管这与化学无关，但它与模式识别和从这些模式中收集的数据的概念密切相关。您认为科学家在 2005 年 8 月 28 日之前第一次看到这张图像时，得出了什么结论？

现在，让我们看一个常见的化学示例。我们都知道金属应该具有化学反应性。我们怎么知道的？嗯，这是金属的一种性质。但是它们的反应性如何？你怎么知道？你现在对元素周期表了解多少，可以帮助你确定这一点？查看表 3.5，看看是否可以收集一些可以巩固您对金属的化学反应性和元素周期表的结论的证据。

表 3.5：有关金属和反应性的信息
金属	大气中的化学反应性
钠	储存在甲苯中，极具反应性
钾	在 O₂ 中燃烧几秒钟
钙	与 O₂ 的反应速度比元素周期表中右边的邻居慢
钛	在形成氧化物屏障后抵抗腐蚀
铝	在形成氧化物屏障后抵抗腐蚀
金	不与氧气反应
铂	不与氧气反应
铜	不与 H₂O 反应；会与 O₂ 缓慢反应
铁	在 O₂ 中生锈

从阅读这张表格中，你能得出什么结论？你能确定金属与空气中的氧气之间的反应在元素周期表中的一行中横向移动时会降低吗？您是否注意到碱金属（第一组）（钠和钾）是所有与氧气反应最强的金属，而碱土金属（第二组）（钙）是第二反应最强的金属？是的，他们是。铝和钛实际上会形成金属氧化物涂层，这就像一层保护盾，防止进一步反应。看看下面的图。铜由于在铜屋顶上形成的这种保护涂层而变成了绿色。你以前见过吗？

目前的温哥华酒店在 1930 年代建造花了十多年时间，因为大萧条暂时中断了建设。从 1939 年到 1972 年，它是温哥华最高的建筑。

这些是什么样的观察？它们是定量的吗？当然不是，因为它们没有附加测量值；它们是定性观察。

其他涉及定量观察的数据类型呢？我们可以查看测量值并确定模式吗？当然可以。统计学家、气象预报员、股市工作人员、体育分析师和化学家（仅举几例职业）每天都会为他们的常规工作执行此操作。如果您试图根据体积置换实验来识别未知物质怎么办。您被提供了一系列已知质量的已知物质，然后您确定它们在水柱中置换了多少体积。通过您的实验，记录了以下数据（表 3.6）。

表 3.6：体积置换数据
物质	质量	置换的水体积
铝	3.7 克	1.0 毫升
铁	7.86 克	1.0 毫升
铜	8.92 克	1.0 毫升
银	10.5 克	1.0 毫升
锌	7.14 克	1.0 毫升
铅	11.34 克	1.0 毫升

首先，仅查看数据表，您认为哪种金属密度最大？您认为是铅还是铝？你怎么知道？铅是正确的答案，因为较重的铅质量置换了相同体积的水。您是否注意到铜比铁重，而铁比锌重？现在您认为这是一种什么样的数据？它是定性的还是定量的？定量是正确的答案，因为我们正在处理测量值。

有趣的是，19.3 克金会置换相同体积的水。它会是密度最大的吗？是的，它会。这也意味着相同量的金转换为约 212.5 磅/加仑。还记得在电视或电影中看到恶棍拿着装满金条的袋子逃跑吗？从这张表中了解金属的密度，这将相当困难。能够阅读表格和数据使我们有能力理解周围的世界。

另一种概括数据趋势并根据这些趋势进行解释的方法是绘制图表。图表就像数字图片，提供实验中收集数据的图像。假设您被要求记录混合物的温度，因为它在热水浴中缓慢加热。您在观察实验时记录了以下数据（表 3.7）。然后您将数据绘制在图表上，看看数字告诉您什么。

表 3.7：时间与温度
时间（秒）	温度 °C
0	23.5
1	24
2	25
3	26
4	27
5	28
6	29
7	30
8	31
9	32

查看图表，您注意到混合物的温度在热水浴中加热时如何变化？它在不断上升。初始点或y−截距代表什么？它是初始温度的值，很可能是室温。使用图表，很明显地看到 y−轴（在本例中为温度）取决于x−轴。对于我们的示例，自变量是时间。这意味着什么？这意味着要进行温度变化，时间必须过去。

能够绘制数值表并阅读相应的图表是一项重要的技能，不仅对数学很重要，而且对科学也很重要。可以使用这些表示形式中的任何一种进行解释；一种可能更直观，因此有时比另一种更容易解释。现在尝试一个示例，您必须绘制图表并进行一些解释。

示例问题：数学成绩与化学成绩

以下数据代表 12 名学生在数学测试和化学测试中的成绩。所有分数均为 50 分。

数学	17	38	40	17	28	30	45	24	48	42	32	36
化学	8	32	36	17	19	20	43	16	48	40	22	29

a. 将此数据绘制在x − y 轴上，以数学成绩作为x 轴。

b. 绘制最佳拟合线。最佳拟合线绘制在散点图上，以便它尽可能多地连接点，并显示数据的总体方向。在构建最佳拟合线时，重要的是大约保持线上下方相同数量的点。

c. 估计在数学测试中获得 32 分的学生的化学成绩。

d. 估计在化学测试中获得 45 分的学生的数学成绩。

e. 根据数据中发现的趋势，您能说出数学成绩和化学成绩之间的关系吗？

解决方案:

(a 和 b)

c) 当学生在数学中获得 32 分时，化学成绩大约为 25 分。我们可以从蓝线上看到这一点。通过对数据进行插值，我们可以从x−轴上的 32 分处向上画一条线，直到最佳拟合线穿过数据点。在这里，我们穿过y−轴，以找到相应的化学成绩。

d) 当学生在化学中获得 45 分时，数学成绩大约为 47 分。我们可以从绿线上看到这一点。通过对数据进行插值，我们可以从y−轴上的 45 分处横向画一条线，直到最佳拟合线穿过数据点。在这里，我们向下画一条线到x−轴，以找到相应的数学成绩。

e) 趋势表明，随着数学成绩的提高，化学成绩也会提高。此图表中的因变量是化学成绩。

用数据进行计算

能够从表格、图表、图片和图表中识别模式是任何科学家和科学学生的宝贵技能。通过拥有图表、图片、表格和图表，您还可以根据自变量和因变量执行各种各样的计算。从这里，我们可以完成诸如进行进一步预测、得出更多结论或识别未知物等任务。例如，让我们说，在前面的密度实验中，我们被提供了实验的未知物。现在，使用相同的图表，但添加第四列，表示金属的密度（表 3.8）。回想一下密度的公式

{\text{Density}}={\frac {\text{mass}}{\text{volume}}}

现在，使用密度公式填充第四列，我们可以看到以下信息。记住密度 = 质量/体积，或者在下面的表格中，第 4 列 = 第 2 列 ÷ 第 3 列。

表 3.6：体积置换数据
物质	质量	置换的水体积	密度
铝	3.7 克	1.0 毫升	2.7 克/毫升
铁	7.86 克	1.0 毫升	7.86 克/毫升
铜	8.92 克	1.0 毫升	8.92 克/毫升
银	10.5 克	1.0 毫升	10.5 克/毫升
锌	7.14 克	1.0 毫升	7.14 克/毫升
铅	11.34 克	1.0 毫升	11.34 克/毫升
未知	1.78 克	0.2 毫升	8.9 克/毫升

仅仅通过这个计算，我们就能确定实验中的未知物吗？当然可以，它是铜。正如你将要学到的，化学中经常使用计算。大多数情况下，你会看到我们会使用各种公式来解决类似于你在任何课程中都会解决的问题。比较答案集之间的关系会让我们了解这类计算的有趣部分。

示例问题

以 7 英里/小时的速度跑 3.5 英里需要多长时间？

解决方案

我们知道

${\text{speed}}={\frac {\text{distance}}{\text{time}}}$

因此

${\text{time}}={\frac {\text{distance}}{\text{speed}}}$

${\text{time}}={\frac {3.5\,{\text{mi}}}{7\,{\text{mi/h}}}}$

${\text{time}}=0.5\,{\text{h}}\,\!$

计算中的另一个重要技巧是从一个单位转换为另一个单位。在化学中，数据经常出现在需要我们使用转换因子才能完成问题的问题中。一些转换因子包括 100 cm = 1 m，1000 mL = 1 L，以及 1 km = 1000 m。

示例问题

光速为 3.00×10⁸ m/s。声速为 1230 km/h。光速比声速快多少。

解决方案:

${\text{speed of sound}}={\frac {1230\,{\text{km}}}{\text{h}}}\times {\frac {1000\,{\text{m}}}{1\,{\text{km}}}}\times {\frac {1\,{\text{h}}}{60\,{\text{min}}}}\times {\frac {1\,{\text{min}}}{60\,{\text{sec}}}}$

${\text{speed of sound}}=342\,{\text{m/s}}\,\!$

${\frac {\text{speed of light}}{\text{speed of sound}}}={\frac {3.00\times 10^{8}\,{\text{m/s}}}{342\,{\text{m/s}}}}$

${\frac {\text{speed of light}}{\text{speed of sound}}}=8.77\times 10^{5}\,\!$

换句话说，光速几乎是声速的 900,000 倍。令人惊叹，不是吗！

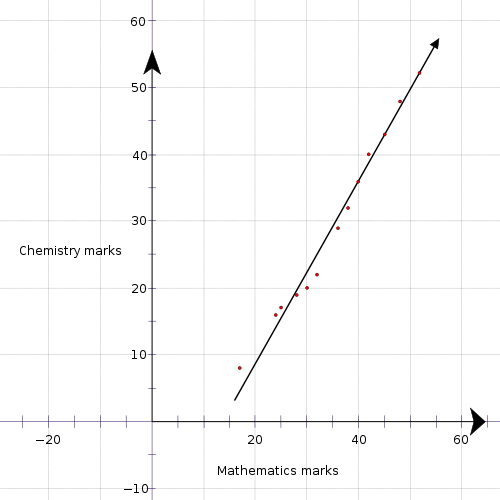
从数据中准备图表

在实验室中，我们大多数时候会收集一些数据，然后把它带回我们的办公桌进行分析。我们想要确定未知固体的熔点，所以我们取一些已知物质的熔点，然后取我们未知物质的熔点；接下来，我们做一张表格，最后把从实验中收集到的数据写入表格。一些我们作为科学家所做的实验室实验要求我们绘制图表，以便解释结果并得出任何结论。绘制任何人都能理解的图表对于任何科学家来说都是一项有用的技能。图表必须在x轴（水平）和y轴（垂直）上进行适当的标记。图表应显示一条直线或一条平滑曲线，表示数据是连续的。直线代表线性关系；曲线则不代表。

示例问题

医疗从业人员长期以来一直在研究心脏。因此，我们现在可以根据从你的年龄得出的公式来计算你的心率。

绘制下面给出的值表。适当标记图表，包括自变量和因变量。将直线一直绘制到y轴，以便找到y截距。最后，在x轴上找到你的年龄，然后通过绘制一条垂直线向上到图表找到你的最大心率。

年龄（岁） (x)	30	40	50	60
每分钟跳动次数 (y) (最大心率)	90	80	70	60

解决方案:

在 17 岁时，从图表上读出的最大心率（每分钟跳动次数）为 103。

从图表中读取结果

化学中的许多性质在绘制时都会导致线性关系。我们在温度/时间关系中看到了这一点。化学中的其他性质不会形成这种线性关系。例如，浓度与温度之间的关系。还记得上次你冲泡速溶咖啡或热巧克力的时候吗？你为什么要把水烧开？如果你使用温水甚至冷水从冰箱里拿出来，会发生什么？撇开预期的口味差异不谈，你想要溶解的固体将会发生什么？你杯子中实际溶解在温水或冷水中的速溶咖啡或热巧克力粉的量，与你使用沸水时相比会很少。这种性质被称为溶解度。物质的溶解度是指它在一定量溶液中可以溶解的量。溶解度受温度影响，但很少是线性的。看看下面的数据表（表 3.9）。这些数据是 KClO₃（氯酸钾）在水中的溶解度。

表 3.9
温度 (°C)	溶解度 (g/100 mL H₂O
0	3.3
20	7.3
40	13.9
60	23.8
80	37.5
100	56.3

现在将数据绘制成图表，看看我们得到的是什么曲线。

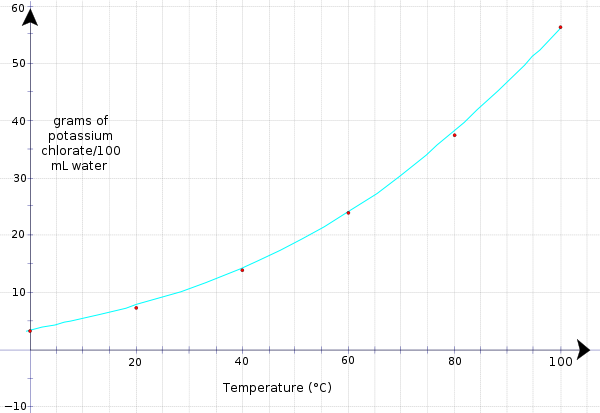
注意，当绘制线条时，溶解在 100 毫升水中氯酸钾的克数与温度之间的关系不是线性的，而是弯曲的。我们仍然可以像之前那样解释数据。例如，当温度为 75 °C 或室温时，KClO₃ 的溶解度（多少 KClO₃）是多少。

使用相同的步骤，我们从 75 °C 向上画一条线，然后横向到 y−轴。读数为 34.5 g/100 mL。因此，在 75 °C 时，34.5 g KClO₃ 可以溶解在 100 mL H₂O 中。

现在你试试一个

示例问题

已知氨气 NH₃ 和氯化钠 NaCl 具有以下溶解度数据（表 3.10）。

表 3.10
温度 (°C)	NH₃ 溶解度 (g/100 mL H₂O)	NaCl 溶解度 (g/100 mL H₂O)
0	88.5	35.7
20	56.0	35.9
40	34.0	36.4
60	20.0	37.1
80	11.0	38.0
100	7.0	39.2

a) 正确绘制每种物质数据的图表。

b) 这些数据中是否有任何是线性的？解释一下。

c) 每种物质在 50 °C 时的溶解度是多少？

解决方案:

a)

b) 当绘制 NaCl 的溶解度数据时，它代表一种线性关系。您可以在上面的图表中看到蓝线。NH₃ 线（红色）是弯曲的；因此它是非线性的。

c) NH₃ 在 50 °C 时的溶解度为 27 g/100 mL H₂O。NaCl 在 50 °C 时的溶解度为 37.5 g/100 mL H₂O。下面的图表被标记，以显示从 50 °C 向上移动的直线，并横向移动到 y-轴（溶解度），以找到这两个部分的答案。

除了绘制和读取线性及非线性数据的图表以得出结论之外，我们还可以做更多的事情。为此，我们使用诸如直线 **斜率** 之类的公式。还记得数学课上的斜率吗？它是一个用于查找一个因素以正或负方式影响另一个因素的速率的公式。还记得数学课上的斜率公式吗？

{\text{slope}}={\frac {\text{rise}}{\text{run}}}\ \ {\text{or}}\ \ m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}

让我们看看如何将斜率公式应用于图表，以了解实验中一个因素是如何影响另一个因素的。

在 19 世纪，热气球的使用作为一项运动以及那些能够负担得起这种奢侈的人们的课外活动非常流行。到目前为止，对气体与温度、压力和体积因素之间关系的研究仅限于罗伯特·波义耳关于压力和体积的实验。雅克·查尔斯在他的关于体积和温度之间关系的实验中脱颖而出。以下是一些典型的来自气体体积/温度实验的数据（表 3.11）。

表 3.11
温度 (°C)	气体体积 (cm³)
20	60
40	65
60	70
80	75
100	80
120	85

现在，找出温度对气体体积的影响。换句话说，找到斜率。选择直线上两点，并使用上面的方程来找到 m 的值。

m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}

m={\frac {80-65}{100-40}}

m={\frac {15}{60}}

m=0.25\,{\text{cm}}^{3}{\text{/}}^{\circ }{\text{C}}\,\!

这意味着什么？这意味着，每升高 1 °C 的温度，体积就会增加 0.25 cm³（或 0.25 mL）。这大约相当于每 4 °C 增加 1 mL。这是一个正向增加（请注意斜率正在增加或向上）。现在让我们再试试一个。

查看表 3.12 中在实验室环境中进行的溴和甲酸之间的一组实验数据。进行该反应是为了查看溴浓度的降低是否会导致反应随后变慢。换句话说，如果从反应中去除一些溴，反应是否会开始变慢？查看数据并看看发生了什么。

表 3.12
读数	溴浓度 (mol/L)	时间
1	0.1	0
2	0.07	0.75
3	0.05	1.75
4	0.035	2.49
5	0.02	3.48
6	0.01	5
7	0.005	6.2
8	0.001	7.5
9	0.0	8.8
10	00	9

查看数据表，你能判断溴浓度的增加是否对反应速率有影响吗？它使反应变快还是变慢？让我们看一下。从 T₁ 到 T₇，溴浓度从 0.1 mol/L 降低到 0.005 mol/L，降低了 0.095 mol/L。这个下降所花费的时间是 6.2 秒。这告诉我们什么关于速率？一个初步结论是，溴浓度的降低会导致反应速率也降低。图表可能会让您更容易根据数据得出结论。

在这里使用斜率来计算影响并不容易，因为我们有一个曲线。我们可以很容易地看到，随着浓度的增加，速率也会增加，但增加了多少？斜率实际上会告诉我们这一点。为了确定曲线的斜率，您需要在曲线上绘制一条 **切线**。切线只是一条绘制到曲线的直线；您可以从此计算斜率。看看下面的图表，切线是用红色钢笔绘制的。

如果我们绘制一条切线，看看，我们得到了一条直线。现在我们可以找到两点。

m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}

m={\frac {0.06-0.07}{1.1-0.75}}

m=-0.028\,{\text{mol/L}}\cdot {\text{s}}\,\!

这意味着随着溴浓度的降低，反应速率也会降低。看看斜率的单位。单位是 mol/L · s。这些是速率的单位。有趣的是，这意味着随着浓度的下降，反应会变慢。

课程总结

数据集中、图片、图表和图形中都可以找到模式。科学家可以从这些模式中对数据进行解释并得出结论。
绘制值表图形时，可以绘制一条直线或一条平滑曲线。某些数据集确实需要最佳拟合线。
最佳拟合线绘制在散点图上，使它尽可能连接更多点，并显示数据的总体方向。在构建最佳拟合线时，还应确保线上方和下方有大致相同数量的点。
当单位不匹配时，需要使用转换系数进行计算。例如，km 和 m。
回顾斜率公式： $m={\tfrac {y_{2}-y_{1}}{x_{2}-x_{1}}}$
对于曲线，请记住先绘制切线，然后求切线的斜率。

复习题

为什么图形的斜率对化学如此重要？
如何找到曲线的斜率？
转换系数用于什么？
以下职业中，哪一种使用数据来识别未知指纹？
(a) 分析化学家

(b) 考古化学家

(c) 无机科学家

(d) 法医科学家

(e) 质量控制化学家
哪个速度最慢？
(a) 200 m/min (200 m/min × 1 km/1000 m = 0.2 km/min)

(b) 0.2 km/min

(c) 10 km/h (10 km/h × 1 h/6 min = 0.17 km/min)

(d) 1.0×10⁵ mm/min (1.0×10⁵ mm/min × 1 m/1000 mm × 1 km/1000 m = 0.1 km/min)

(e) 10 mi/h (10 mi/h × 1.603 km/mi × 1h/60 min = 0.267 km/min or 0.27 km/min)
安德鲁正在完成他的化学实验室考试的密度实验室。他在数据表（表 3.13）中收集了以下数据。
表 3.13
固体质量 (g) 溶液体积 (mL)
3.4 0.3
6.8 0.6
10.2 0.9
21.55 1.9
32.89 2.9
44.23 3.9
55.57 4.9

(a) 绘制图形以表示数据。

(b) 计算斜率。

(c) 线的斜率代表什么？

(d) 你能帮助安德鲁通过查阅标准表来确定他的未知物吗？
唐娜正在完成她实验的最后一步，以找出氨浓度对反应的影响。她从计时试验中收集了以下数据，并准备进行分析（表 3.14）。唐娜现在需要绘制数据图，描述关系，找到斜率，然后讨论斜率的含义。帮助唐娜解释她的数据。
表 3.14
时间（秒）浓度 (mol/L)
0.20 49.92
0.40 39.80
0.60 29.67
0.81 20.43
1.08 14.39
1.30 10.84
1.53 5.86
2.00 1.95
2.21 1.07
2.40 0.71
2.60 0.71

词汇表

碱金属: 元素周期表中的第 1 族金属（H、Li、Na、K、Rb、Cs、Fr）。
碱土金属: 元素周期表中的第 2 族金属（Be、Mg、Ca、Sr、Ba、Ra）。
化学反应性: 根据元素或化合物在反应性（或活性）序列中的位置，对其行为的观察结果。
转换系数: 用于将一个单位转换为另一个单位的比率。
因变量: 根据另一个变量而变化的变量（y 轴变量）。
图形: 使用坐标系（x − y 轴）对模式进行图形表示。
自变量: 导致另一个变量变化的变量（x 轴变量）。
最佳拟合线: 绘制在图形上的线，使它尽可能连接更多点，并显示数据的总体方向。在构建最佳拟合线时，还应确保线上方和下方有大致相同数量的点。
线性关系: x 值与 y 值成比例变化的关系，导致一条直线。
非线性关系: x 值与 y 值不成比例变化的关系，导致一条曲线。
斜率: 用于查找一个因素影响另一个因素的速率的公式。
溶解度: 特定量溶液中可以溶解的物质的量。
切线: 绘制到曲线的直线。
y 轴截距: 直线与 y 轴的交点。

← Making Measurements · How Scientists Use Data →

此材料改编自原始 CK-12 图书，可在此处找到。本作品根据知识共享署名-相同方式共享 3.0 美国许可协议进行授权

表 3.13
固体质量 (g)	溶液体积 (mL)
3.4	0.3
6.8	0.6
10.2	0.9
21.55	1.9
32.89	2.9
44.23	3.9
55.57	4.9

表 3.14
时间（秒）	浓度 (mol/L)
0.20	49.92
0.40	39.80
0.60	29.67
0.81	20.43
1.08	14.39
1.30	10.84
1.53	5.86
2.00	1.95
2.21	1.07
2.40	0.71
2.60	0.71