IB 物理/热物理
热能从高温物体传递到低温物体。
T(K) = t/(°C) +273
将摄氏温度转换为开氏温度,需要加上 273.15。将开氏温度转换为摄氏温度,需要减去 273.15。
| 概念 | 解释 |
|---|---|
| 温度 | 是物质中分子平均动能的量度。 |
| 内能 | 是物质中平均动能和势能的量度。 |
| 热能 | 是系统与其周围环境之间非机械的能量传递。 |
| 词语 | 定义 |
|---|---|
| 摩尔 | 含有与 12g 碳-12 中原子数目相同的粒子的物质的量。 |
| 摩尔质量 | 一摩尔物质的质量。 |
| 阿伏伽德罗常数 | 是每摩尔粒子数。该数值可以在 IB 物理数据手册中找到,等于 6.023 × 1023。 |
| 词语 | 定义 |
|---|---|
| 比热容(SHC) | 1kg 物质升高 1K 温度所需的热能。 |
| 热容 | 物质升高 1K 温度所需的热能。 |
| 相态 | 解释 |
|---|---|
| 固态 | 宏观上,体积和形状固定。分子围绕平均位置振动。 |
| 液态 | 体积固定,但形状可变。分子振动,但不固定在某个位置。分子可以自由移动。 |
| 气态 | 分子会膨胀以充满容器。分子不处于固定位置。 |
| 相变 | 解释 |
|---|---|
| 凝固 | 运动较慢的液体分子开始失去能量,并固定在某个位置。液体转变为固体。 |
| 熔化 | 固定的固体分子获得能量,并开始运动得更多。固体转变为液体。 |
| 蒸发 | 液体表面运动较快的分子逃逸,使液体冷却。液体转变为气体。 |
| 沸腾 | 液体内部运动较快的分子逃逸。液体转变为气体。 |
| 冷凝 | 运动较慢的气体分子失去能量。气体转变为液体。 |
相变与分子势能的增加或减少有关,而不是动能。因此,在相变过程中温度不变。
蒸发发生在液体的表面,而沸腾发生在整个液体中。
比潜热是相变过程中每单位质量吸收或释放的能量。
其中,
L= 比潜热,单位 Jkg^-1
Q= 能量,单位 J
m= 质量,单位 kg
压力是作用在单位面积上的力。它以帕斯卡为单位。
假设
- 牛顿定律适用于分子行为
- 不存在分子间力
- 分子是点
- 碰撞是弹性的
- 这些碰撞不花费时间
温度是理想气体分子平均随机动能的量度
| 定律 | 对理想气体的影响 |
|---|---|
| 压强定律 | 气体的压强与其温度成正比 |
| 查理定律 | 气体的体积与其温度成正比 |
| 玻意耳定律 | 气体的压强与其体积成反比 |
麦克斯韦-玻尔兹曼分布曲线
气体的速度(或能量)分布曲线通常以速度为横轴,分子数量为纵轴。曲线从原点开始,上升到峰值,然后呈指数下降,就像横轴是一条渐近线一样。较高的温度曲线更“平坦”,峰值更低,但在峰值之后下降速度更慢。
蒸发是单个分子从液体中逃逸的过程。这发生在任何液体中,除非液体处于封闭系统中,否则最终所有液体都会蒸发。
随着液体蒸发,其温度会降低。冷却效应是由于快速移动的分子逃逸,留下缓慢移动的分子。这意味着分子的平均速度降低,因此液体的温度降低。这是蒸发冷却的原理。
线性膨胀系数用符号 a 表示,定义了物体(例如一根金属丝)的长度在给定的温度变化下变化多少。它用于公式 ΔL = a x L0 x ΔT,其中 L0 是初始长度,ΔL 是变化量。
重要的是要理解,L0 应该出现在这个公式中。膨胀是由于分子移动得更快,因此在振动时距离更远。因此,分子越多,在给定变化情况下膨胀越大,因为所有分子之间的空间都会膨胀。
固体的热膨胀是由于组成粒子的振动幅度增加。随着温度升高(即热量增加),粒子获得更多能量,这些能量变成 Ek(尽管不是平移能量),导致振动幅度更大。因此,分子之间有更大的空间,因此整个固体变得更大。
线性膨胀方程可以应用于任何方向(在大多数物质中),因此可以用来计算面积和体积的膨胀。要计算面积,只需计算两个垂直方向的膨胀,然后计算这两个变化导致的面积变化。对于体积,计算三个垂直方向的膨胀,然后计算体积变化。
利用热膨胀
- 双金属片(其中两条不同的金属片,具有不同的 a 值,在中间粘合在一起),当加热或冷却时会弯曲(因为其中一侧的金属膨胀/收缩速度快于另一侧)。这可以用来闭合或断开电路,通常用于恒温器(即当温度低于或高于某个温度时会打开或关闭加热器的装置)。
- 当金属环膨胀时,外边缘和中间的孔都会膨胀(这可能并不明显,但这是真的)。因此,可以扩大“孔”使环可以套在某个物体上,然后当它冷却时会锁紧。这种技术用于将带子安装在马车轮上(如今这种情况很少见)。
- 液体的体积膨胀是水银温度计和酒精温度计的基础。随着温度升高,水银的体积增加,将其推向管子上方。
克服热膨胀问题
- 桥梁由混凝土块建造,如果温度升高,它们会相互膨胀并破碎。为了克服这个问题,在块之间留有间隙,以便它们膨胀。这就是桥梁上存在间隙的原因,也是您开车经过桥梁时听到“砰砰”声的原因。铁路轨道也是如此。
- 蒸汽管道必须允许膨胀,因为它们在温度上有很大变化(即,管道里有蒸汽时和没有蒸汽时)。为了允许这种情况,管道连接到“角落”接头。这些接头类似于 L 形,因此垂直管道可以在接头中上下膨胀,而水平管道可以在左右膨胀,而不会扭曲管道的形状(它还会创建一系列膨胀发生的短部分,而不是一个长部分,这将更难处理)。
10.3 : 热力学
[edit | edit source]10.3.1
[edit | edit source]热力学用于描述热力学系统不同部分中热力学变量之间的关系。热力学变量的主要例子是热量、功和熵,但还有很多其他变量,如压力、体积、表面张力、磁化率和(摩尔)浓度。所有这些变化都在系统内部和外部热量、功和熵的传递背景下进行研究。经典热力学完全关注平衡状态,因此其方程中不出现带有时间维度的量。只有时间的顺序可能会出现(之前,之后)。64.134.223.225 (discuss) 02:08, 26 August 2014 (UTC)
10.3.2
[edit | edit source]热量和功都是能量的形式,因此,加热物体或对物体做功会导致能量的传递。A 对 B 做功,会增加 B 的内能,同时减少 A 的内能,依此类推。
10.3.3
[edit | edit source]热力学中的系统是指具有特定内能的物体。
例如,一块金属块就是一个系统。可以向其中加入热量或从其中取出热量。对它做功的概念有点模糊,但可以想象。
一定质量的气体也可以是一个系统。热量可以进出,如果你压缩它,你就在做功(从而增加内能),如果气体做功(即被允许膨胀,但推动活塞回来或其他情况),那么它的内能就会减少。
热力学过程是指从系统中取出或输入热量,或对系统做功或由系统做功的任何过程。
10.3.4
[edit | edit source]如果快速压缩气体,则其温度会升高。压缩气体所做的功已转换为内能。如果然后让气体冷却,与功所提供的能量量相等的热量将释放到周围环境中。
如果允许气体膨胀,则会发生相反的情况。温度(和内能)会降低,然后系统会从周围环境中吸收热量。换句话说,系统会做功(膨胀),导致内能损失,但如果让系统这样做,它会吸收回热量。
功在第一种情况下转换为热量,热量在第二种情况下转换为功。
10.3.5
[edit | edit source]等温 : 等温过程是指内能(或温度)没有变化的过程。这种过程的一个例子可能是非常缓慢地膨胀或压缩气体,这样在对系统做功或由系统做功时,会从周围环境中吸收或释放热量。因此,即使做功并传递热量,温度也会保持恒定。在等温过程中,所做的功和传递出去的热量必须以相同的速度向相反的方向发生。
绝热 : 绝热过程是指 ΔQ 为零(即没有热量离开或进入系统)的过程。最常见的例子是快速压缩或膨胀气体,这样就没有时间传递热量。在这样的过程中,内能(即温度)会在做功时发生变化。
等容 : 等容过程是指 ΔV 为零(即体积变化为零)的过程。在这样的过程中,系统所做的功为零。一个例子是将只包含空气的密闭锡罐放入火中。在第一近似中,罐子不会膨胀,唯一的变化是气体获得内能,这可以通过其温度和压力的升高来证明。在数学上,ΔQ = ΔU。
等压 : 等压过程是指压力保持恒定的过程。一个简单的例子是加热一锅没有盖子的水,这样水表面就会受到恒定压力(大气压力)。
10.3.6
[edit | edit source]在 P-V 图(压力与体积)上说明这些热力学过程是另一件事,如果使用图表会更好。
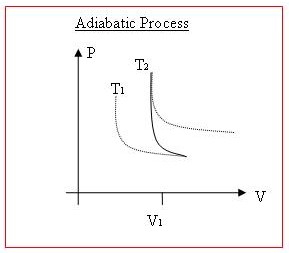
当对气体做功或由气体做功,或当热量传递进或出气体时,体积和压力通常都会发生变化。P 与 V 图上等温线的曲线在 x 轴和 y 轴都有渐近线。温度更高的曲线远离原点。
等温过程将完全遵循这些温度曲线之一,因为内能是恒定的。
对于绝热过程,当对系统做功时,温度会升高,因此图上的点会“向上”移动到更高的温度曲线。如果由系统做功,则点会“向下”移动到更低的温度曲线。
除此之外,P 与 V 图上产生的曲线通常由过程的性质决定。有时只有压力会发生变化(可以添加更多气体,或者温度可以发生变化),有时只有体积会发生变化(温度会随着体积减小而降低,保持压力恒定)。
还值得注意的是(虽然我不知道是否必要),曲线下的面积等于系统所做的功(这在下一节中会变得令人困惑)。
10.3.7
[edit | edit source]ΔU = ΔQ + ΔW
这个方程将热量和功的变化与内能的变化联系起来。实际符号有点棘手,但如果我们知道正 ΔU 值会导致温度升高,就可以记住。基于此,我们知道通过向系统添加热量,温度会升高,因此当向系统添加热量时,ΔQ 为正。
类似地,如果对系统做功,温度会升高,因此对系统做功时,ΔW 为正。显然,当热量释放到周围环境中时,ΔQ 为负,当系统做功时,ΔW 为负。
这个方程可以通过代入两个值并求出第三个值来应用。由于我们知道 ΔU 为零,因此这个方程可以在等温过程中简化,并且由于我们知道 ΔQ 为零,因此它可以在绝热过程中简化。
10.3.8
[edit | edit source]热力学循环是指一系列热力学过程最终使系统恢复到初始状态,从该状态可以重复该过程。这个概念被热机所利用,热机使用一系列重复的热力学过程来从热能产生机械能。热机主要有两种类型(内燃机和外燃机),下面将对它们进行描述。
外燃机 : 这些是老式的发动机,用于蒸汽火车。热量用于将水煮沸,水变成蒸汽,从而增加管道中的压力。这种压力增加会迫使活塞向下移动(活塞连接到适合发动机正在做的事情的任何东西)。一旦它被完全压下,一个阀门就会释放,蒸汽被允许逸出到另一组管道中,最终通过冷凝器返回到锅炉。这会降低压力,活塞被其他活塞在凸轮轴中的作用或弹簧推回。当它再次到达顶部时,更多的蒸汽被允许进入,迫使活塞再次向下移动。也可以使用涡轮机,其中蒸汽用于旋转涡轮机,从而产生旋转运动(这通常用于发电)。我认为我们真正需要知道的就是这些,内燃机在这里更重要。
内燃机:这是一种目前汽车中常用的发动机类型,汽油在汽缸内被点燃。它们被称为四冲程发动机,因为整个过程发生在两个循环中(两次向上冲程和两次向下冲程)。活塞从汽缸顶部开始向下移动。进气门打开,汽缸内吸入燃料和氧气的混合物。当活塞到达底部时,进气门关闭,活塞向上移动,压缩混合物,直到活塞到达顶部。当活塞处于顶部时,火花塞点燃混合物,产生向下的高压,推动活塞向下(这是发动机实际做功的地方)。当活塞到达底部时,排气门打开,活塞向上移动时排出废气。到达顶部后,排气门关闭,进气门打开(回到起点)。所有这些过程都可以用 P-V 图表示(有人想画一个吗?)。大多数物理教科书中会有一个类似的图表。
熵(符号 S)是衡量系统混乱程度的指标。关于概率、亚态和信息论,有一个复杂的解释,但我认为没有必要。基本上,熵总是增加的。在一个系统中可以降低熵,但它会导致该系统周围环境的熵增加。这是热力学第二定律;自然系统趋向于向更混乱的状态发展。从能量的角度来看,混乱程度的增加意味着能量分布更均匀。如果有一个高能量点和一个低能量点,可以使用这两个点之间的能量差做功,熵会降低这种能量差。换句话说,能量趋于均匀分布,而不是集中在一个点上。
自然系统趋向于向更混乱的状态发展(热力学第二定律)。这意味着你无法制造出一种发动机,它可以将输入到它的能量的 100% 转换为功(即,没有发动机可以达到 100% 的效率)。例如,第一定律表明,放在桌子上的木块可以将其热能的一部分转换为功,并从桌子上跳下来,但第二定律说这不可能发生(不是说它不能发生,只是它非常非常不可能)。
此外,由于它不适合放在任何其他地方,但出现在数据手册中,方程 ΔS = ΔQ/ΔT 可以用来求解熵的变化(其中 Q = 热量,T = 温度)。这实际上是一个微积分方程,但对于 T 的微小变化,用平均温度近似就足够了。
冰箱:基本原理是通过做功克服熵,在内部产生一个低温区域,而在外部产生一个高温区域。这个过程通过一套沿着系统外壁和内壁运行的管道来实现。低压(因此冷)气体通过内壁管道,吸收冰箱内部的热量。然后,使用冷凝器(活塞)对该气体进行加压,并通过外壁管道进行抽送。由于该气体进行了做功,热量从该气体释放到冰箱外部。然后,慢慢地让气体通过连接到低压管道的阀门进行再循环。这样,即使内部温度已经很低,热量还是从内部转移到外部。这似乎违反了第二定律,但宇宙的总熵实际上正在增加,因为让它发生需要能量(驱动冷凝器)。这种系统的效率由方程 效率 = QH-QL / QL 定义,其中效率是指冰箱的效率(1 表示完美或 100% 效率),QL 是低温(内部)温度,QH 是高温(外部)温度。
热泵:热泵是一种特殊的加热器,通常与 HVAC 系统中的空调功能一起安装,当预期的气候变化使其比安装和使用直接加热器更经济时。热泵不是依靠热量的纯粹产生,而是将热量(更准确地说,是热能)从一个地方转移到另一个地方。热泵的工作原理是通过做功将热量从寒冷的外部转移到温暖的内部。这与上面描述的冰箱正好相反。这种泵的效率将为 效率 = QH-QL / QH,与上述工作原理相同。
请注意,在每种情况下,这个方程都类似于数据手册中的方程,但分母必须根据特定过程要实现的目标进行选择。
如果我们想从哲学角度看待问题,可以将熵视为定义时间的“向前”和“向后”的因素。随着时间的推移,熵增加,因此我们可以将时间视为熵增加时向前推进。如上所述,热泵和冰箱能够降低系统中的熵,但会增加整个系统 + 环境的熵。当冰(或其他东西)融化时,它会吸收热量,因此熵会增加。从固态到液态到气态的转变也标志着熵的增加,因为粒子变得越来越随机地运动。