无机化学/化学键/轨道杂化

四个sp³轨道。

三个sp²轨道。

在化学中，杂化（或杂交）是将原子轨道混合成新的杂化轨道的概念，这些轨道适用于电子配对以形成价键理论中的化学键。杂化轨道在解释分子几何形状和原子键合特性方面非常有用。

历史和用途

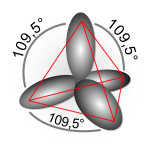
化学家莱纳斯·鲍林首先发展了杂化理论，以解释甲烷（CH₄）等分子的结构。鲍林指出，碳原子通过使用一个s轨道和三个p轨道形成四个键，因此“可以推断”碳原子将使用p轨道形成三个直角键，并使用s轨道在某个任意方向形成第四个较弱的键。然而，实际上，甲烷具有四个强度相等的键，它们之间以109.5°的四面体键角分开。鲍林解释说，在存在四个氢原子的情况下，s和p轨道形成了四个等价的组合或杂化轨道，每个轨道都用sp³表示以指示其组成，这些轨道沿四个C-H键方向排列。从历史上看，这个概念是为这种简单的化学体系而发展的，但后来该方法被更广泛地应用，如今它被认为是合理化有机化合物结构的有效启发式方法。它给出了一个与路易斯结构等价的简单轨道图像。杂化理论主要用于有机化学。

杂化理论是有机化学的一个组成部分。对于绘制反应机理，有时需要一个经典的键合图像，其中两个原子共享两个电子。杂化理论解释了烯烃和甲烷中的键合。主要由轨道杂化决定的p特性或s特性的数量可用于可靠地预测分子性质，例如酸度或碱度。

概述

轨道是电子在分子中行为的模型表示。在简单杂化的例子中，这种近似基于原子轨道，类似于氢原子获得的那些，氢原子是唯一一个对其薛定谔方程有精确解析解的原子。在较重的原子（如碳、氮和氧）中，使用的原子轨道是2s和2p轨道，类似于氢的激发态轨道。

假设杂化轨道是原子轨道的混合物，以不同的比例叠加在一起。例如，在甲烷中，形成每个C-H键的C杂化轨道包含25%的s特性和75%的p特性，因此被称为sp³（读作s-p-three）杂化。量子力学将这种杂化描述为形式为N[s + (√3)pσ]的sp³波函数，其中N是归一化常数（此处为1/2），pσ是沿C-H轴方向的p轨道，形成σ键。p与s的比率（一般用λ表示）在此示例中为√3，N²λ² = 3/4为p特性或p分量的权重。

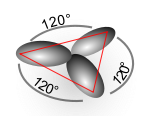
通常情况下，同一原子上的任意两个杂化轨道都必须相互正交。对于一个原子，其s和p轨道形成杂化轨道h_i和h_j，夹角为$\theta$，正交条件意味着以下关系：1 + $\lambda$_i$\lambda$_j cos($\theta$) = 0。杂化轨道i的p-s比为$\lambda$_i²，杂化轨道j的p-s比为$\lambda$_j²。正如Bent规则所述，指向更具电负性的取代基的键往往具有更高的p特性。在同一原子上的等价杂化轨道的特殊情况下，同样夹角为$\theta$，该方程简化为1 + $\lambda$² cos($\theta$) = 0。例如，BH₃具有三角平面几何形状，三个120°键角，硼原子周围有三个等价杂化轨道，因此1 + $\lambda$² cos($\theta$) = 0 变为 1 + $\lambda$² cos(120°) = 0，得到$\lambda$² = 2 作为p-s比。换句话说，sp²杂化。

杂化类型

sp³

对于四面体配位的碳（例如，甲烷CH₄），碳应该有4个轨道，具有正确的对称性来与4个氢原子成键。

碳的基态电子构型为1s² 2s² 2p²，或者更容易理解为

C	↑↓	↑↓	↑	↑
	1s	2s	2p	2p	2p

（注意：1s轨道的能量低于2s轨道，2s轨道的能量低于2p轨道）

碳原子可以使用其两个单占据的p型轨道与两个氢原子形成两个共价键，生成亚甲基CH₂单线态，这是卡宾中最简单的例子。碳原子还可以通过将一个电子从双占据的2s轨道激发到空的2p轨道，从而形成四个单占据轨道，与四个氢原子成键。

C*	↑↓	↑	↑	↑	↑
	1s	2s	2p	2p	2p

形成两个额外键释放的能量超过了所需的激发能，在能量上更有利于形成四个C-H键。

从量子力学的角度来看，如果四个键是等价的，则可以获得最低的能量，这需要它们是由碳上的等价轨道形成的。可以得到一组四个等价轨道，它们是价层（核心轨道几乎从未参与成键）s和p波函数的线性组合，即四个sp³杂化轨道。

C*	↑↓	↑	↑	↑	↑
	1s	sp3	sp3	sp3	sp3

在CH₄中，四个sp³杂化轨道与氢的1s轨道重叠，生成四个σ（西格玛）键（即四个长度和强度相同的单共价键）。

转化为

sp²

其他碳基化合物和其他分子可以用类似甲烷的方式解释。例如，乙烯 (C₂H₄) 在两个碳原子之间有一个双键。其路易斯结构如下所示

乙烯的路易斯结构。每个碳原子与两个氢原子键合，碳原子之间有一个双键。

对于该分子，碳原子进行sp²杂化，因为碳原子之间的双键需要一个π键，并且每个碳原子只形成三个σ键。在sp²杂化中，2s轨道只与三个可用的2p轨道中的两个混合

C*	↑↓	↑	↑	↑	↑
	1s	sp2	sp2	sp2	2p

形成总共三个sp²轨道和一个剩余的p轨道。在乙烯中，两个碳原子通过两个sp²轨道的重叠形成σ键，并且每个碳原子通过s–sp²重叠与氢形成两个共价键，所有键角均为120°。碳原子之间垂直于分子平面的π键由2p–2p重叠形成。氢-碳键的强度和长度都相等，这与实验数据相符。

sp

诸如炔烃之类的具有三键的化合物的化学键合可以通过sp杂化来解释。在这个模型中，2s轨道只与三个p轨道中的一个混合，

C*	↑↓	↑	↑	↑	↑
	1s	sp	sp	2p	2p

产生两个sp轨道和两个剩余的p轨道。乙炔 (C₂H₂) 的化学键合包括两个碳原子之间的sp–sp重叠形成σ键，以及由p–p重叠形成的两个额外的π键。每个碳原子还以180°角的σs–sp重叠与氢键合。

杂化和分子形状

杂化有助于解释分子形状，因为键之间的角度（大约）等于杂化轨道之间的角度。

不同类型的杂化轨道的形状

sp^x杂化

由于主族元素的价电子轨道是一个s轨道和三个p轨道，并遵循相应的八隅体规则，因此sp^x杂化用于模拟这些分子的形状。

配位数	形状	杂化	例子
2	线性	sp杂化 (180°)	CO2
3	平面三角形	sp2杂化 (120°)	BCl3
4	四面体	sp3杂化 (109.5°)	CCl4
轨道间角	$\theta =\arccos \left(-{\frac {1}{x}}\right)$

sp^xd^y杂化

由于过渡金属的价电子轨道是五个d轨道、一个s轨道和三个p轨道，并遵循相应的18电子规则，因此sp^xd^y杂化用于模拟这些分子的形状。由于涉及不同的d轨道，这些分子往往具有对应于相同杂化的多种形状。由于p轨道不一定完全占据，因此平面正方形形状具有16个价电子。

配位数	形状	杂化	例子
4	平面正方形	sp2d杂化	PtCl42−
5	三角双锥	sp3d杂化	Fe(CO)5
	四方锥		MnCl52−
6	八面体	sp3d2杂化	Mo(CO)6
7	五角双锥	sp3d3杂化	ZrF73−
	顶帽八面体		MoF7−
	顶帽三角棱柱		TaF72−
8	四方反棱柱	sp3d4杂化	ReF8−
	十二面体		Mo(CN)84−
	双顶帽三角棱柱		ZrF84−
9	三顶帽三角棱柱	sp3d5杂化	ReH92−
	顶帽四方反棱柱

sd^x杂化

在某些d电子数低的过渡金属配合物中，p轨道未被占据，并且sd^x杂化用于模拟这些分子的形状。

配位数	形状	杂化	例子
3	三角锥形	sd2杂化 (90°)	CrO3
4	四面体	sd3杂化 (70.5°, 109.5°)	TiCl4
5	四方锥	sd4杂化 (65.9°, 114.1°)	Ta(CH3)5
6	C3v 三角棱柱	sd5杂化 (63.4°, 116.6°)	W(CH3)6
轨道间角	$\theta =\arccos \left(\pm {\sqrt {{\frac {1}{3}}\left(1-{\frac {2}{x}}\right)}}\right)$

超价分子的杂化

八隅体扩展

在一些普通化学教科书中，使用保林首先提出的“扩展八隅体”方案，利用d轨道来呈现主族AX₅及以上化合物的杂化。然而，鉴于计算化学计算的结果，这种方案现在被认为是不正确的。

配位数	形状	杂化	例子
5	三角双锥	sp3d杂化	PF5
6	八面体	sp3d2杂化	SF6
7	五角双锥	sp3d3杂化	IF7

1990年，Magnusson发表了一篇具有开创性的著作，明确排除了d轨道杂化在第二周期元素超价化合物键合中的作用。长期以来，在使用分子轨道理论描述这些分子时，这是一个有争议和令人困惑的问题。这里部分混淆源于这样一个事实，即必须在用于描述这些化合物的基组中包含d函数（否则会导致不合理的能量和扭曲的几何形状），并且d函数对分子波函数的贡献很大。历史上，这些事实被解释为意味着d轨道必须参与键合。然而，Magnusson在他的著作中得出结论，d轨道的参与与超价无关。

共振

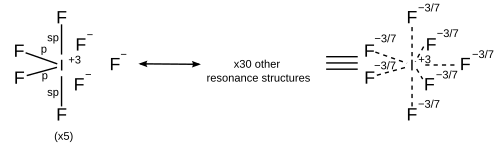
根据计算化学，更好的处理方法是除了杂化之外，还要引入σ键共振，这意味着每个共振结构都有其自身的杂化方案。所有共振结构都必须遵循八隅体规则。

配位数	共振结构
5	三角双锥
6	八面体
7	五角双锥

计算VB理论中的杂化

虽然轨道杂化的简单模型常用于解释分子形状，但在现代价键程序中，杂化的使用方法有所不同。具体来说，杂化不是先验确定的，而是通过变分优化来寻找最低能量解，然后进行报告。这意味着所有人为的约束，特别是两个约束，都被取消了

• 杂化被限制为整数（等价杂化）
• 杂化轨道彼此正交（杂化缺陷）

这意味着在实践中，杂化轨道并不符合通常教授的简单概念，因此在科学计算论文中，为了表达它们的性质，通常简单地将其称为sp^x、sp^xd^y或sd^x杂化，而不是更具体的整数数值。

等价杂化

尽管理想的杂化轨道很有用，但实际上大多数键需要中间性质的轨道，类似于中间离子-共价特性。这需要扩展以包含每种类型（s、p、d）原子轨道的灵活权重，并在分子几何形状偏离理想键角时，允许对键形成进行定量描述。p成分的含量不受限于整数；即，sp^2.5之类的杂化也很容易描述。

键轨道的杂化由Bent规则决定：“原子s成分集中在指向正电性取代基的轨道上”。

对于具有孤对电子的分子，成键轨道是等价的sp^x杂化。例如，水中氧的两个成键杂化轨道可以描述为sp^4.0，以得到104.5°的轨道间角。这意味着它们具有20%的s成分和80%的p成分，并且不意味着杂化轨道是由氧原子上的一个s轨道和四个p轨道形成的，因为氧的2p亚层仅包含三个p轨道。

杂化缺陷

s和p轨道杂化形成有效的sp^x杂化需要它们具有相当的径向范围。虽然2p轨道的平均尺寸比2s轨道大不到10%，部分原因是2p轨道缺乏径向节点，但具有一个径向节点的3p轨道比3s轨道大20-33%。s和p轨道的范围差异在同一族中进一步增加。可以通过考虑局域分子轨道来分析化学键中原子的杂化，例如在自然键轨道（NBO）方案中使用自然局域分子轨道。在甲烷CH₄中，计算出的p/s比率约为3，与“理想”sp³杂化一致，而对于硅烷SiH₄，p/s比率更接近于2。其他2p元素也观察到类似的趋势。用氟取代氢进一步降低了p/s比率。2p元素表现出接近理想的杂化，具有正交的杂化轨道。对于较重的p区元素，不能证明这种正交性的假设。库泽尔尼格将这些与理想杂化的偏差称为杂化缺陷。

然而，Gerratt、Cooper和Raimondi（SCVB）以及Shaik和Hiberty（VBSCF）等计算VB小组更进一步地论证，即使对于甲烷、乙烯和乙炔等模型分子，杂化轨道也已经存在缺陷且非正交，例如甲烷的杂化是sp^1.76而不是sp³。

光电子能谱

关于轨道杂化的一个误解是，它错误地预测了许多分子的紫外光电子能谱。虽然如果将库普曼斯定理应用于局域杂化，这是正确的，但量子力学要求（在这种情况下是离子化的）波函数服从分子的对称性，这意味着价键理论中的共振。例如，在甲烷中，离子化态（CH₄⁺）可以由四个共振结构构成，将弹出的电子归因于四个sp³轨道中的每一个。这四个结构的线性组合，保持结构数量不变，导致三倍简并的T₂态和一个A₁态。离子化态与基态之间的能量差将是电离能，这会产生两个与实验一致的值。

存在两种不同的CH₄⁺态（A₁和T₂），它们都是由CH₄的电离产生的。这导致了甲烷光电子能谱上的两个独特峰。

局域MOs与正则MOs

由杂化原子轨道形成的成键轨道可以被认为是局域分子轨道，可以通过适当的数学变换，由分子轨道理论的离域轨道形成。对于基态分子，轨道的这种变换不会改变总的多电子波函数。因此，基态的杂化轨道描述与基态总能量和电子密度以及对应于最小总能量值的分子几何形状的离域轨道描述等价。

两种局域表示

H₂O的对称性适应和杂化的孤对电子

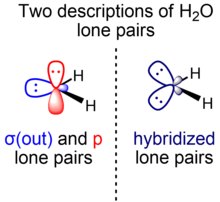
具有多重键或多个孤对电子的分子可以具有用σ和π对称性或等价轨道表示的轨道。不同的价键方法使用两种表示方法中的任何一种，它们具有数学上等价的总多电子波函数，并且通过占据分子轨道集的酉变换相关联。

对于多重键，σ-π表示法比等价轨道（弯曲键）表示法更为普遍。相反，对于多个孤对电子，大多数教科书使用等价轨道表示法。但是，σ-π表示法也使用，例如Weinhold和Landis在自然键轨道的背景下使用，自然键轨道是一种局域轨道理论，包含经典（价键/路易斯结构）成键对和孤对的现代化类似物。例如，对于氟化氢分子，两个F孤对电子本质上是未杂化的p轨道，而另一个是sp^x杂化轨道。类似的考虑适用于水（一个O孤对电子位于纯p轨道中，另一个位于sp^x杂化轨道中）。