跳转到内容

无机化学/化学键/VSEPR理论

Add links
来自维基教科书，开放的书籍，开放的世界
< 无机化学 | 化学键
最新修订版本于2022年4月10日审查。有模板/文件更改正在等待审查。

价层电子对互斥理论（VSEPR）是一个化学模型，用于根据中心原子周围的电子对数量来预测单个分子的几何形状。[1] 它也被称为吉莱斯皮-尼霍尔姆理论，以其两位主要开发者罗纳德·吉莱斯皮和罗纳德·尼霍尔姆命名。

VSEPR理论的前提是，原子周围的价层电子对倾向于相互排斥，因此它们将采用一种使这种排斥最小化的排列方式。这反过来又降低了分子的能量并增加了其稳定性，从而决定了分子的几何形状。

历史

[编辑 | 编辑源代码]

分子几何形状与价层电子数（包括共用电子对和非共用电子对）之间相关性的想法，最早由内维尔·西德威克和赫伯特·鲍威尔于 1940 年在牛津大学的贝克莱恩演讲中提出。[2] 1957 年，伦敦大学学院的罗纳德·吉莱斯皮和罗纳德·西德尼·尼霍尔姆完善了这一概念，建立了一个更详细的理论，能够在各种替代几何形状之间进行选择。[3][4]

概述

[编辑 | 编辑源代码]

VSEPR 理论用于预测分子中中心原子周围电子对的排列方式，尤其是简单对称的分子。在本理论中，中心原子被定义为与两个或多个其他原子键合的原子，而末端原子仅与另一个原子键合。[5]:398 例如，在异氰酸甲酯 (H3C-N=C=O) 分子中，两个碳和一个氮是中心原子，而三个氢和一个氧是末端原子。[5]:416 中心原子的几何形状及其非键合电子对反过来又决定了整个分子更大结构的几何形状。

中心原子价层电子对的数量是在绘制分子的路易斯结构之后确定的，并将路易斯结构扩展以显示所有键合基团和孤对电子。[5]:410–417 在 VSEPR 理论中，双键或三键被视为单个键合基团。[5] 中心原子键合的原子数与中心原子非键合价电子形成的孤对数之和称为中心原子的空间数。

电子对（如果存在多重键，则为基团）被认为位于以中心原子为中心的球体的表面上，并且倾向于占据位置，以最大限度地减小它们之间的相互排斥，从而最大限度地增加它们之间的距离。[5]:410–417[6] 因此，电子对（或基团）的数量决定了它们将采用的整体几何形状。例如，当中心原子周围有两个电子对时，它们之间的相互排斥在它们位于球体的相对两极时最小。因此，中心原子预计将采用线性几何形状。如果中心原子周围有 3 个电子对，它们的排斥可以通过将它们放置在以原子为中心的等边三角形的顶点上以最小化。因此，预测的几何形状是三角形。同样，对于 4 个电子对，最佳排列是四面体。[5]:410–417

作为预测给定数量的电子对所采用的几何形状的工具，一种经常使用的是利用充气的气球来物理演示最小电子对排斥原理。通过操作，气球会获得轻微的表面静电荷，这会导致它们在将它们绑在一起时采用与相应数量的电子对大致相同的几何形状。例如，五个绑在一起的气球将采用三角双锥体几何形状，就像 PCl5 分子的五个键合对一样。

空间数

[编辑 | 编辑源代码]
四氟化硫的空间数为 5。

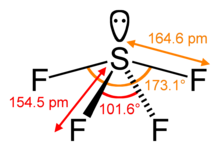
分子中中心原子的空间数是与该中心原子键合的原子数，称为配位数，加上中心原子上的孤对价电子数。[7] 例如，在 SF4 分子中，中心硫原子有四个配体；硫的配位数为 4。除了四个配体外，硫在这个分子中还有一个孤对。因此，空间数为 4 + 1 = 5。

排斥程度

[编辑 | 编辑源代码]

整体几何形状通过区分键合和非键合电子对进一步细化。在与相邻原子形成σ键中共享的键合电子对比该原子的非键合（孤对）电子对更远离中心原子，非键合电子对靠近其带正电荷的原子核。因此，VSEPR 理论认为孤对的排斥大于键合对的排斥。因此，当一个分子具有 2 种不同排斥程度的相互作用时，VSEPR 理论预测结构，其中孤对占据允许它们经历较少排斥的位置。孤对 - 孤对 (lp–lp) 排斥被认为比孤对 - 键合对 (lp–bp) 排斥更强，而孤对 - 键合对 (lp–bp) 排斥被认为比键合对 - 键合对 (bp–bp) 排斥更强，这些区别指导关于整体几何形状的决定，当 2 个或多个非等效位置是可能的时。[5]:410–417 例如，当 5 个价层电子对围绕中心原子时，它们将采用三角双锥体分子几何形状，具有两个共线的轴向位置和三个赤道位置。轴向位置的电子对只有三个相邻的赤道对，距离只有 90°，而第四个对距离 180° 远得多，而赤道电子对只有两个相邻对在 90° 处，两个在 120° 处。来自距离 90° 的近邻对的排斥更为重要，因此轴向位置经历的排斥比赤道位置更多；因此，当存在孤对时，它们倾向于占据赤道位置，如下一节中针对空间数为 5 的示意图所示。[6]

孤对电子和成键电子之间的差异也可以用来解释理想几何形状的偏差。例如，H2O 分子在其价层中有四个电子对：两个孤对电子和两个成键电子对。这四个电子对分布开来，大致指向四面体的顶点。然而，两个 O-H 键之间的键角只有 104.5°，而不是规则四面体的 109.5°，因为两个孤对电子（其密度或概率包络更靠近氧原子核）比两个成键电子对施加更大的相互排斥。[5]:410–417[6]

具有较高键序的键也施加更大的排斥力，因为 π 键电子参与其中。[6] 例如，在异丁烯 (H3C)2C=CH2 中，H3C-C=C 角 (124°) 大于 H3C-C-CH3 角 (111.5°)。然而，在碳酸根离子 CO2−3 中，由于共振，所有三个 C-O 键都是等效的，角度为 120°。

AXE 方法

[edit | edit source]

在应用 VSEPR 理论时，通常使用电子计数的“AXE 方法”。中心原子周围的电子对用公式 AXnEm 表示，其中 A 代表中心原子，总是隐含下标 1。每个 X 代表一个配体（与 A 键合的原子）。每个 E 代表中心原子上的一个孤对电子。[5]:410–417 X 和 E 的总数称为空间位阻数。例如，在分子 AX3E2 中，原子 A 的空间位阻数为 5。

当取代基 (X) 原子不完全相同时，几何形状仍然大致有效，但键角可能与所有外部原子都相同的键角略有不同。例如，烯烃如 C2H4 中的双键碳是 AX3E0，但键角并不完全都是 120°。同样，SOCl2 是 AX3E1，但由于 X 取代基并不相同，因此 X-A-X 角并不完全相等。

根据空间位阻数以及 X 和 E 的分布，VSEPR 理论做出了以下表格中的预测。

主族元素

[edit | edit source]

对于主族元素，存在立体化学活性孤对电子 E，其数量可以在 0 到 3 之间变化。请注意，几何形状是根据原子位置而不是电子排列命名的。例如，将 AX2E1 描述为弯曲分子意味着三个原子 AX2 不在一条直线上，尽管孤对电子有助于确定几何形状。

空间位阻
数		 分子几何形状[8]
0 个孤对电子		 分子几何形状[5]:413–414
1 个孤对电子		 分子几何形状[5]:413–414
2 个孤对电子		 分子几何形状[5]:413–414
3 个孤对电子
2
线性
      
3
平面三角形
弯曲
    
4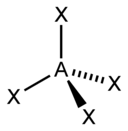
四面体
三角锥形
弯曲
  
5
三角双锥
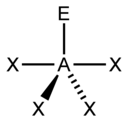跷跷板
T 形
线性
6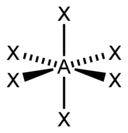
八面体
四方锥形
平面四方
  
7
五角双锥
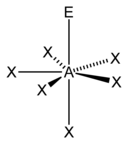五角锥形
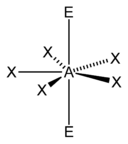五角平面
  
8
四方反棱柱
 		    
分子
类型		 形状[5]:413–414 电子排列[5]:413–414
包括孤对电子，以浅黄色显示 		几何形状[5]:413–414
不包括孤对电子 		示例
AX2E0 线性 BeCl2,[1] CO2[6]
AX2E1 弯曲 NO2-,[1] SO2,[5]:413–414 O3,[1] CCl2
AX2E2 弯曲 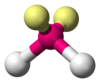H2O,[5]:413–414 OF2[9]:448
AX2E3 线性 XeF2,[5]:413–414 I3-,[9]:483 XeCl2
AX3E0 平面三角形 BF3,[5]:413–414 CO2−3,[9]:368 NO3-,[1] SO3[6]
AX3E1 三角锥形 NH3,[5]:413–414 PCl3[9]:407
AX3E2 T 形 ClF3,[5]:413–414 BrF3[9]:481
AX4E0 四面体 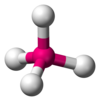CH4,[5]:413–414 PO3−4, SO2−4,[6] ClO4-,[1] XeO4[9]:499
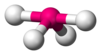
AX4E1 跷跷板或双锥 SF4[5]:413–414[9]:45
AX4E2 平面四方 XeF4[5]:413–414
AX5E0 三角双锥 PCl5[5]:413–414
AX5E1 四方锥形 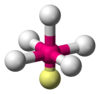ClF5,[9]:481 BrF5,[5]:413–414 XeOF4[6]
AX5E2 五角平面 XeF5-[9]:498
AX6E0 八面体 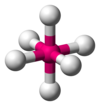SF6[5]:413–414
AX6E1 五角锥形 XeOF5-,[10] IOF2−5[10]
AX7E0 五角双锥[6] IF7[6]
AX8E0 正方形反棱柱[6] IF8-

过渡金属（Kepert 模型）

[edit | edit source]

过渡金属原子上的孤对电子通常是立体化学惰性的，这意味着它们的存在不会改变分子几何形状。例如，六水合配合物 M(H2O)6 对 M = V3+, Mn3+, Co3+, Ni2+ 和 Zn2+ 都是八面体形的，尽管中心金属离子的电子构型分别是 d2, d4, d6, d8 和 d10。 [9]:542 Kepert 模型忽略了过渡金属原子上的所有孤对电子，因此所有这些原子的周围几何形状对应于 AXn 的 VSEPR 几何形状，其中有 0 个孤对电子 E。 [11][9]:542 这通常写成 MLn，其中 M = 金属，L = 配体。Kepert 模型预测了配位数为 2 到 9 的以下几何形状

分子
类型		 形状 几何形状 示例
ML2 线性 HgCl2[1]
ML3 平面三角形
ML4 四面体 NiCl2−4
ML5 三角双锥 Fe(CO)5
四方锥形 MnCl52−
ML6 八面体 WCl6[9]:659
ML7 五角双锥形[6] ZrF3−7
帽状八面体 MoF7-
帽状三角棱柱 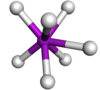TaF2−7
ML8 正方形反棱柱[6] ReF8-
十二面体 Mo(CN)4−8
双帽状三角棱柱 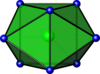ZrF4−8
ML9 三帽状三角棱柱 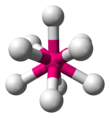ReH2−9[9]:254
帽状正方形反棱柱

示例

[edit | edit source]

甲烷分子 (CH4) 是四面体形的，因为它有四对电子。四个氢原子位于四面体的顶点，键角为 cos−1(−1⁄3) ≈ 109° 28′。 [12][13] 这被称为 AX4 型分子。如上所述，A 代表中心原子，X 代表外原子。 [5]:410–417

氨分子 (NH3) 有三对参与键合的电子，但氮原子上有一对孤对电子。 [5]:392–393 它没有与其他原子键合；然而，它通过排斥作用影响着整体形状。如上所述的甲烷，有四个电子密度的区域。因此，电子密度的区域的整体方向是四面体形的。另一方面，只有三个外原子。这被称为 AX3E 型分子，因为孤对电子用 E 表示。 [5]:410–417 根据定义，分子形状或几何形状仅描述原子核的几何排列，对 NH3 而言为三角锥形。 [5]:410–417

7 或更高的空间数是可能的，但不太常见。空间数 7 发生在七氟化碘 (IF7) 中；空间数为 7 的基本几何形状是五角双锥形。 [6] 空间数为 8 的最常见几何形状是正方形反棱柱几何形状。 [14]:1165 例如，八氰合钼酸盐 (Mo(CN)4−8) 和八氟合锆酸盐 (ZrF4−8) 阴离子。 [14]:1165 钾九氢合铼酸盐中的九氢合铼酸根离子 (ReH2−9) 是具有空间数为 9 的化合物的罕见例子，它具有三帽状三角棱柱几何形状。 [9]:254[14]

空间数为 10、11、12 或 14 的可能几何形状分别是双帽状正方形反棱柱（或双帽状十二面体）、十八面体、二十面体和双帽状六角反棱柱。没有化合物具有涉及单齿配体的这种高空间数，而涉及多齿配体的化合物通常可以更简单地分析为具有较低空间数的配合物，当一些多齿配体被视为一个单元时。 [14]:1165,1721

例外

[edit | edit source]

有一些化合物组，VSEPR 无法预测正确的几何形状。

一些 AX2E0 分子

[edit | edit source]

较重 14 族元素炔烃类似物（RM≡MR，其中 M = Si、Ge、Sn 或 Pb）的形状经计算为弯曲的。 [15][16][17]

一些 AX2E2 分子

[edit | edit source]

一个例子是氧化锂分子 Li2O，它是线性的而不是弯曲的，这归因于键合本质上是离子性的，导致锂原子之间发生强烈的排斥作用。 [18]
另一个例子是 O(SiH3)2，其 Si-O-Si 角为 144.1°，与 Cl2O (110.9°)、(CH3)2O (111.7°) 和 N(CH3)3 (110.9°) 中的角度相比。Gillespie 的解释是，当配体具有与中心原子相似或大于中心原子的电负性时，孤对电子的定位最强，因此它们排斥其他电子对的能力也最强。[19] 当中心原子电负性更强时，如 O(SiH3)2 中，孤对电子定位较差，排斥作用较弱。这一事实，加上更强的配体-配体排斥力（-SiH3 相比于上面的例子是一个相对较大的配体），导致了比预期更大的 Si-O-Si 键角。[19]

一些 AX6E1 和 AX8E1 分子

[edit | edit source]
六氟化氙，具有扭曲的八面体几何结构

一些 AX6E1 分子，例如六氟化氙 (XeF6) 和 Te(IV) 和 Bi(III) 阴离子，TeCl2−6，TeBr2−6，BiCl3−6，BiBr3−6 和 BiI3−6，是八面体而不是五角锥体，孤对电子对几何形状的影响程度不如 VSEPR 预测的那样。[20] 一种解释是，配体的空间拥挤不允许非键合孤对电子存在；[19] 另一种解释是惰性电子对效应。[21] 同样地，八氟合氙酸根离子 (XeF2−8) 在亚硝酰八氟合氙(VI) 中[9]:498[22][23] 是一个正方反棱柱，而不是一个双顶三角棱柱（如 VSEPR 理论预测的 AX8E1 分子），尽管它有一个孤对电子。

平面正方形 ML4 配合物

[edit | edit source]

Kepert 模型预测 ML4 过渡金属分子呈四面体形状，它无法解释平面正方形配合物的形成。[9]:542 大多数此类配合物表现出 d8 电子构型，例如四氯合铂酸根 (PtCl2−4) 离子。平面正方形配合物形状的解释涉及电子效应，需要使用晶体场理论。[9]:562-4

具有强 d 电子贡献的配合物

[edit | edit source]
六甲基钨，一个几何结构不同于主族配位的过渡金属配合物。

一些 d 电子数较少的过渡金属配合物具有不寻常的几何结构，这可以归因于 d 亚层键合相互作用。[24] Gillespie 发现这种相互作用产生键合对，这些键合对也占据了球体的相应对位点（与配体相对）。[25][26] 这种现象是由于 sdx 杂化轨道双叶形结构导致的电子效应。[27][28] 这些键合对的排斥导致了一组不同的形状。

分子类型 形状 几何形状 示例
ML2 弯曲 VO+2
ML3 三角锥形 CrO3
ML4 四面体 TiCl4[9]:598–599
ML5 四方锥形 Ta(CH3)5[29]
ML6 C3v 三角棱柱 W(CH3)6[30]

第二主族较重元素 (即钙、锶和钡卤化物，MX2) 的三原子卤化物的气相结构并非如预测的那样是线性的，而是弯曲的 (近似 X–M–X 角：CaF2，145°；SrF2，120°；BaF2，108°；SrCl2，130°；BaCl2，115°；BaBr2，115°；BaI2，105°)。[31] Gillespie 提出，这也是由于配体与金属原子 d 亚层的键合相互作用导致的，从而影响了分子几何形状。[19][32]

奇电子分子

[edit | edit source]

VSEPR 理论可以扩展到具有奇数个电子的分子，方法是将未配对电子视为“半个电子对”。实际上，奇电子对几何形状的影响类似于完整的电子对，但影响较小，因此几何形状可能介于具有完整电子对的分子和中心原子少一个电子对的分子之间。

例如，二氧化氮 (NO2) 是一个 AX2E0.5 分子，中心氮原子有一个未配对电子。VSEPR 预测的几何形状类似于 NO2- 离子 (AX2E1，弯曲，键角约为 120°)，但介于 NO2- 和 NO+2 (AX2E0，线性，180°) 之间。实际上，NO2 是弯曲的，角度为 134°，更接近 120° 而不是 180°，这与理论定性一致。

同样地，二氧化氯 (ClO2，AX2E1.5) 的几何形状类似于 ClO2-，但介于 ClO2- 和 ClO+2 之间。

最后，甲基自由基 (CH3) 预计像甲基阴离子 (CH3-) 一样是三角锥形的，但键角更大，如同三角平面甲基阳离子 (CH+3)。然而，在这种情况下，VSEPR 预测并不完全正确，因为 CH3 实际上是平面的，尽管它扭曲成三角锥形几何结构只需要很少的能量。[33]

参考文献

[edit | edit source]
  1. ↑ a b c d e f g Jolly, W. L. (1984). 现代无机化学. McGraw-Hill. pp. 77–90. ISBN 978-0-07-032760-3.
  2. ↑ http://rspa.royalsocietypublishing.org/content/176/965/153.abstract N.V.Sidgwick 和 H.M.Powell, Proc.Roy.Soc.A 176, 153–180 (1940) Bakerian 讲座。立体化学类型和价键组
  3. ↑ R.J.Gillespie 和 R.S.Nyholm, Quart.Rev. 11, 339 (1957)
  4. ↑ R.J.Gillespie, J.Chem.Educ. 47, 18(1970)
  5. ↑ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae Petrucci, R. H.; W. S., Harwood; F. G., Herring (2002). 普通化学：原理与现代应用 (第 8 版). Prentice-Hall. ISBN 978-0-13-014329-7.
  6. ↑ a b c d e f g h i j k l m n Miessler, G. L.; Tarr, D. A. (1999). 无机化学 (第 2 版). Prentice-Hall. pp. 54–62. ISBN 978-0-13-841891-5.
  7. ↑ Miessler, G. L.; Tarr, D. A. (1999). 无机化学 (第 2 版). Prentice-Hall. p. 55. ISBN 978-0-13-841891-5.
  8. ↑ Petrucci, R. H.; W. S., Harwood; F. G., Herring (2002). 普通化学：原理与现代应用 (第 8 版). Prentice-Hall. pp. 413–414 (表 11.1). ISBN 978-0-13-014329-7.
  9. ↑ a b c d e f g h i j k l m n o p q r Housecroft, C. E.; Sharpe, A. G. (2005). 无机化学 (第 2 版). Pearson. ISBN 978-0-130-39913-7.
  10. ↑ a b Baran, E. (2000). "五角锥形 XeOF5- 和 IOF2−5 阴离子的平均振动幅度". J. Fluorine Chem. 101: 61–63. doi:10.1016/S0022-1139(99)00194-3.
  11. ↑ Anderson, O. P. (1983). "书评：无机立体化学（作者：David L. Kepert）" (PDF). Acta Crystallographica B. 39: 527–528. doi:10.1107/S0108768183002864. Retrieved 14 September 2020. 基于对电子对排斥的常见观点的系统定量应用
  12. ↑ Brittin, W. E. (1945). "四面体碳原子的价键角". J. Chem. Educ. 22 (3): 145. Bibcode:1945JChEd..22..145B. doi:10.1021/ed022p145.↑ "四面体两条边的夹角" Template:Webarchive – Maze5.net
  13. ↑ a b c d Wiberg, E.; Holleman, A. F. (2001). 无机化学. Academic Press. ISBN 978-0-12-352651-9.
  14. ↑ Power, Philip P. (2003 年 9 月). "乙炔的硅、锗、锡和铅类似物". Chem. Commun. (17): 2091–2101. doi:10.1039/B212224C. PMID 13678155.
  15. ↑ Nagase, Shigeru; Kobayashi, Kaoru; Takagi, Nozomi (2000 年 10 月 6 日). "重第 14 族元素之间的三键。理论方法". J. Organomet. Chem. 11 (1–2): 264–271. doi:10.1016/S0022-328X(00)00489-7.
  16. ↑ Sekiguchi, Akira; Kinjō, Rei; Ichinohe, Masaaki (2004 年 9 月). "含硅-硅三键的稳定化合物" (PDF). Science. 305 (5691): 1755–1757. Bibcode:2004Sci...305.1755S. doi:10.1126/science.1102209. PMID 15375262. S2CID 24416825. [失效链接]
  17. ↑ LiOLi 分子的键长光谱测定：强离子键，D. Bellert，W. H. Breckenridge，J. Chem. Phys. 114，2871 (2001)；doi:10.1063/1.1349424
  18. ↑ a b c d 分子几何模型，Gillespie R. J.，Robinson E.A. Chem. Soc. Rev.，2005，34，396–407，doi: 10.1039/b405359c
  19. ↑ Wells A.F. (1984) 结构无机化学 第 5 版 牛津科学出版物 ISBN 0-19-855370-6
  20. ↑ Template:Housecroft2nd
  21. ↑ Peterson, W.; Holloway, H.; Coyle, A.; Williams, M. (1971 年 9 月). "氙周围的反棱柱配位：硝酰八氟合氙(VI)的结构". Science. 173 (4003): 1238–1239. Bibcode:1971Sci...173.1238P. doi:10.1126/science.173.4003.1238. ISSN 0036-8075. PMID 17775218. {{cite journal}}: Cite has empty unknown parameter: |month= (help)
  22. ↑ Hanson, Robert M. (1995). 分子折纸：精确比例模型，纸制. University Science Books. ISBN 0-935702-30-X.
  23. ↑ Kaupp, Martin (2001). ""非 VSEPR" 结构和 d0 系统中的键合". Angew. Chem. Int. Ed. Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#.
  24. ↑ Gillespie, Ronald J.; Noury, Stéphane; Pilmé, Julien; Silvi, Bernard (2004). "对第 4 周期金属 Ca 至 Mn 的 d0 分子几何的电子局域化函数研究". Inorg. Chem. 43 (10): 3248–3256. doi:10.1021/ic0354015. PMID 15132634.
  25. ↑ Gillespie, R. J. (2008). "VSEPR 模型的五十年". Coord. Chem. Rev. 252 (12–14): 1315–1327. doi:10.1016/j.ccr.2007.07.007.
  26. ↑ Landis, C. R.; Cleveland, T.; Firman, T. K. (1995). "Making sense of the shapes of simple metal hydrides". J. Am. Chem. Soc. 117 (6): 1859–1860. doi:10.1021/ja00111a036.
  27. ↑ Landis, C. R.; Cleveland, T.; Firman, T. K. (1996). "Structure of W(CH3)6". Science. 272 (5259): 179–183. doi:10.1126/science.272.5259.179f.
  28. ↑ King, R. Bruce (2000). "Atomic orbitals, symmetry, and coordination polyhedra". Coord. Chem. Rev. 197: 141–168. doi:10.1016/s0010-8545(99)00226-x.
  29. ↑ Haalan, A.; Hammel, A.; Rydpal, K.; Volden, H. V. (1990). "The coordination geometry of gaseous hexamethyltungsten is not octahedral". J. Am. Chem. Soc. 112 (11): 4547–4549. doi:10.1021/ja00167a065.
  30. ↑ Template:Greenwood&Earnshaw
  31. ↑ Seijo, Luis; Barandiarán, Zoila; Huzinaga, Sigeru (1991). "Ab initio model potential study of the equilibrium geometry of alkaline earth dihalides: MX2 (M=Mg, Ca, Sr, Ba; X=F, Cl, Br, I)" (PDF). J. Chem. Phys. 94 (5): 3762. Bibcode:1991JChPh..94.3762S. doi:10.1063/1.459748. hdl:10486/7315.
  32. ↑ Anslyn E.V. and Dougherty D.A., Modern Physical Organic Chemistry (University Science Books, 2006), p.57
Retrieved from "https://wikibooks.cn/w/index.php?title=Inorganic_Chemistry/Chemical_Bonding/VSEPR_theory&oldid=4046776"
华夏公益教科书