化学工程过程导论/示例：带循环的简单系统

带循环的系统：清洁过程

问题陈述

示例:

考虑一个过程，其中新开采的矿石需要进行清洁，以便后期的加工单元不会被泥土污染。每小时有 3000 公斤的脏矿石被倾倒进一个大型洗矿机，在洗矿机中，水被允许浸泡矿石，直到矿石流到该单元底部的排水口。在此过程之后，矿石上残留的泥土量可以忽略不计，但水仍然吸附在矿石表面，因此清洗后的矿石的净质量流量为每小时 3100 公斤。

脏水在一个沉降器中被净化，该沉降器能够去除流中 90% 的泥土，而不会去除大量的水。然后，净化后的流与新鲜水流混合，然后再进入洗矿机。

湿润的清洁矿石进入干燥机，在干燥机中，所有的水都被去除。干燥的矿石以每小时 2900 公斤的速度从干燥机中取出。

该过程的设计示意图如下

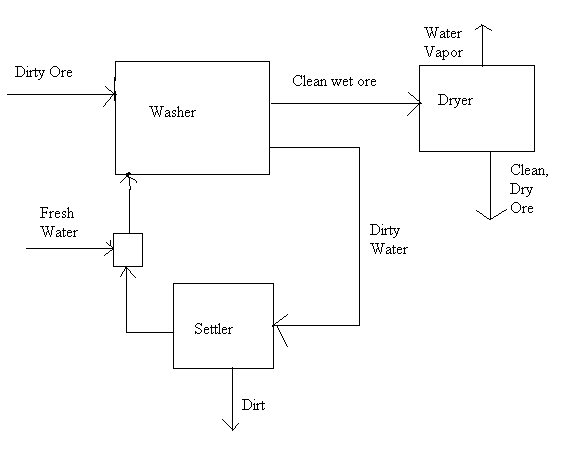
a) 计算在稳态下实现这种去除所需的淡水质量流量。

b) 假设泥土在水中的溶解度为$0.4{\frac {g{\mbox{ dirt}}}{cm^{3}{\mbox{ H}}_{2}O}}$. 假设离开洗矿机的水是泥土饱和的，计算进入洗矿机的流中泥土的质量分数（在与新鲜水流混合之后）。

第一步：绘制流程图

问题陈述中给出了一个示意图，但它非常不完整，因为它不包含任何设计规范（沉降器的效率、泥土在水中的溶解度以及质量流量）。因此，强烈建议您即使在提供给您时也绘制自己的图片。确保您标记所有流和未知浓度。

第二步：自由度分析

• 围绕洗矿机：6 个独立未知数 ($x_{O1},{\dot {m}}_{2},x_{D2},{\dot {m}}_{3},x_{D3},x_{O4}$)，三个独立的质量平衡（矿石、泥土和水）以及一个溶解度。洗矿机具有2 个自由度。
• 围绕干燥机：2 个独立未知数 ($x_{O4},{\dot {m}}_{5}$) 以及两个独立的方程 = 0 个自由度。

• 围绕沉降器：5 个独立未知数 (${\dot {m}}_{3},x_{D3},{\dot {m}}_{7},{\dot {m}}_{8},x_{D8}$)，两个质量平衡（泥土和水），饱和泥土的溶解度，以及一个额外的信息（去除 90% 的泥土），给我们留下了1 个自由度。
• 在混合点：我们需要包括这一点来计算该过程的总自由度，因为否则我们不会在任何地方计算 m9。5 个未知数 (${\dot {m}}_{2},x_{D2},{\dot {m}}_{8},x_{D8},{\dot {m}}_{9}$) 以及 2 个质量平衡，给我们留下了3 个自由度。

因此，总共 = 3+2+1 - 6 个中间变量（不包括 xO4，因为它进入干燥机）= 0

问题定义明确。

制定计划

回想一下，我们的思路是寻找一个具有 0 自由度的单元操作或多个单元操作的组合，计算这些变量，然后重新计算自由度，直到所有变量都被考虑在内。

从我们的初始分析来看，干燥机有 0 个 DOF，因此我们可以计算出两个未知数 xO4 和 m5。现在我们可以认为 xO4 和 m5 已知，并对单元操作重新进行自由度分析。

• 在洗涤器周围：现在我们只有 5 个未知数 ($x_{O1},{\dot {m}}_{2},x_{D2},{\dot {m}}_{3},x_{D3}$)，但仍然只有三个方程式和溶解度。1 DOF。
• 在沉降器周围：由于 xO4 和 m5 与该操作无关，因此这里没有任何变化。
• 整体系统：由于 ${\dot {m}}_{5}$ 已经确定，我们有三个未知数 ($x_{O1},{\dot {m}}_{7},{\dot {m}}_{9}$)，并且我们有三个物料衡算（矿石、泥土和水）。因此，整个系统的 0 DOF。

现在我们可以说我们知道 $x_{O1},{\dot {m}}_{7},$ 和 ${\dot {m}}_{9}$。

• 再次在沉降器周围：由于我们知道 m7，因此沉降器现在有 0 DOF，我们可以求解 ${\dot {m}}_{3},x_{D3},{\dot {m}}_{8},$ 和 $x_{D8}$。

• 再次在洗涤器周围：现在我们知道 m8 和 xD8。我们可以写多少个物料衡算方程式？

因此，洗涤器有两个未知数 (m2，xD2) 和两个方程式（泥土和水的物料衡算方程式）= 0 DOF

最后一步也可以通过对混合点的物料衡算方程式来完成（如下所示）。一旦我们获得 m2 和 xD2，系统就完全确定了。

单位换算

唯一单位不一致的给定信息是溶解度，它是以 $0.4{\frac {g{\mbox{ dirt}}}{cm^{3}{\mbox{ H}}_{2}O}}$ 给出的。但是，由于我们知道水的密度（或可以查询），我们可以将它转换为 ${\frac {kg{\mbox{ dirt}}}{kg{\mbox{ H}}_{2}O}}$，如下所示

$0.4{\frac {g{\mbox{ dirt}}}{cm^{3}{\mbox{ H}}_{2}O}}*1{\frac {cm^{3}{\mbox{ H}}_{2}O}{g{\mbox{ H}}_{2}O}}=0.4{\frac {g{\mbox{ dirt}}}{g{\mbox{ H}}_{2}O}}=0.4{\frac {kg{\mbox{ dirt}}}{kg{\mbox{ H}}_{2}O}}$

现在，由于这些信息与质量流量的单位相同，我们可以继续下一步。

执行计划

首先，对干燥器进行任何两个质量平衡。我选择总量和矿石平衡。请记住，第三个平衡与前两个不独立！

• 总量平衡: ${\dot {m}}_{4}={\dot {m}}_{5}+{\dot {m}}_{6}$
• 矿石平衡: ${\dot {m}}_{4}*x_{O4}={\dot {m}}_{5}*x_{O5}+{\dot {m}}_{6}*x_{O6}$

代入已知值

• 总量: $3100={\dot {m}}_{5}+2900$
• 矿石: $x_{O4}*3100=1*2900$

求解得到

${\dot {m}}_{5}=200{\frac {kg}{hr}}$

$x_{O4}=0.935{\frac {kg}{hr}}$

现在我们已经完成了干燥器，我们执行计划中的下一步，即总系统平衡

• 水平衡: ${\dot {m}}_{9}={\dot {m}}_{5}$
• 矿石平衡: $x_{O1}*{\dot {m}}_{1}={\dot {m}}_{6}$
• 泥土平衡: $(1-x_{O1})*{\dot {m}}_{1}={\dot {m}}_{7}$

${\dot {m}}_{9}=200{\frac {kg}{hr}}$, $x_{O1}=0.967$,

${\dot {m}}_{7}=100{\frac {kg}{hr}}$

接下来我们按照计划进入沉降器，这个有点棘手，因为解决方案并不立即显而易见，但必须解一个系统。

• **总平衡**: ${\dot {m}}_{3}={\dot {m}}_{7}+{\dot {m}}_{8}$
• **泥土平衡**: ${\dot {m}}_{3}*x_{D3}={\dot {m}}_{7}*x_{D7}+{\dot {m}}_{8}*x_{D8}$
• **去除效率**: ${\dot {m}}_{7}=0.9*{\dot {m}}_{3}*x_{D3}$

使用溶解度稍微棘手。您可以通过注意到流3 中的泥土质量与水的质量成正比来使用它，因此您可以写成

• 流3 中的泥土质量 = 流3 中的水质量 * 0.4
• **溶解度**: ${\dot {m}}_{3}*x_{D3}=0.4*{\dot {m}}_{3}*(1-x_{D3})$

代入已知值，得到以下方程组

• ${\dot {m}}_{3}=100+{\dot {m}}_{8}$
• ${\dot {m}}_{3}*x_{D3}=100+{\dot {m}}_{8}*x_{D8}$
• ${\dot {m}}_{3}*x_{D3}=111.11$
• ${\dot {m}}_{3}*x_{D3}=0.4*{\dot {m}}_{3}*(1-x_{D3})$

求解这四个未知数的方程，解为

${\dot {m}}_{3}=388.89{\frac {kg}{hr}},{\dot {m}}_{8}=288.89{\frac {kg}{hr}},$

$x_{D3}=0.286,x_{D8}=0.0385$

最后，我们可以转到混合点，并说

• 总计: ${\dot {m}}_{8}+{\dot {m}}_{9}={\dot {m}}_{2}$
• 泥土: ${\dot {m}}_{8}*x_{D8}={\dot {m}}_{2}*x_{D2}$

由此得出最终的未知数

${\dot {m}}_{2}=488.89{\frac {kg}{hr}}$

$x_{D2}=0.0229$

由于问题要求 ${\dot {m}}_{2}$，我们现在已经完成了。

检查你的工作

这些值应该通过使用数值绘制一个新的流程图并确保洗涤器上的平衡满足来进行检查。留作读者的练习。