循环反应非常有用,主要原因是它们可以用于提高多种反应的选择性,将反应推到其平衡转化率之外,或通过去除产物来加速催化反应。与反应器耦合的循环回路通常包含分离过程,其中未反应的反应物从产物中(部分)分离出来。然后,这些反应物与新鲜进料一起送回反应器。
示例:
考虑一个用于将乙烯加氢成乙烷的系统


反应进行得太慢,无法完成(并释放出过多的热量),因此设计人员决定实施一个循环系统,其中在反应仅部分完成之后,混合物被送入膜分离器。在那里,大多数乙烯被分离出来,氢或乙烯的污染很少。分离后,清洁的物流进入分离器,其中剩余混合物的一部分返回反应器,其余部分被丢弃。
该过程的系统规格如下
- 进料:584 千克/小时乙烯,200 千克/小时氢气
- 反应器出口物流中氢的质量分数为 15%
- 膜分离器的物流:100 千克/小时,氢气 5%,乙烷 93%
- 分离器:30% 弃料,70% 回流
该系统的反应程度是多少?如果没有分离/循环过程,反应程度会是多少?(假设离开反应器的氢气的质量分数相同)什么限制了该过程的有效性?
解决方案:
让我们首先像往常一样绘制流程图
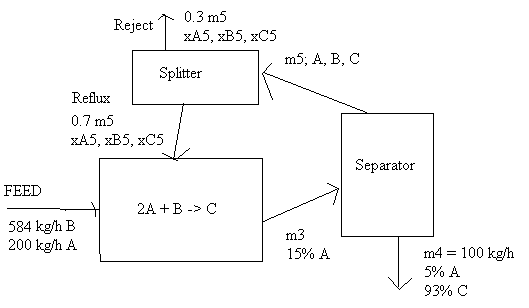
- 在反应器上:6 个未知数
 - 3 个方程式 = 3 个自由度
- 3 个方程式 = 3 个自由度
- 在分离器上:5 个未知数
 - 3 个方程式 = 2 个自由度
- 3 个方程式 = 2 个自由度
- 在分离器上:3 个未知数 - 0 个方程式(我们用它们全部标记图表)-> 3 个自由度
- 重复变量:8 (
 出现两次,
出现两次, 出现一次)
出现一次)
- 总 DOF = 8 - 8 = 0 DOF
通常,尽管并非总是如此,但处理反应器本身最后是最容易的,因为它通常具有最多的未知数。让我们先看看整个系统,因为我们经常可以从那里获得一些有价值的信息。
整个系统 DOF(整个系统)= 4 个未知数 ( ) - 3 个方程式 = 1 个自由度。
) - 3 个方程式 = 1 个自由度。
|
注意
我们不能说 A 和 B 的总质量是守恒的,因为这里有一个反应!因此,我们必须将转化率 X 包含在反应器和整个系统的未知数列表中。但是,系统中的总质量是守恒的,所以我们可以求解  . .
|
让我们继续求解 m5,因为它在后面会很有用。


在不知道转换率的情况下,我们无法对整个系统进行任何操作,所以让我们看看其他地方。
DOF(分离器) = 4 个未知数 ( ) - 3 个方程 = 1 个 DOF。 尽管如此,让我们还是尝试求解我们能求解的那些变量。
) - 3 个方程 = 1 个 DOF。 尽管如此,让我们还是尝试求解我们能求解的那些变量。
我们可以求解 m3,因为从分离器上的整体物料衡算可以得出



然后,我们可以对 A 进行物料衡算,以求解 xA5



由于我们不知道  或
或  ,我们无法使用分离器上的 B 或 C 的物料衡算,所以让我们继续前进。现在让我们转向反应器。
,我们无法使用分离器上的 B 或 C 的物料衡算,所以让我们继续前进。现在让我们转向反应器。
DOF:剩余 3 个未知数 ( ) - 2 个方程(因为整体衡算已经求解!)= **1 个 DOF**。 因此,我们仍然无法完全求解反应器。 然而,我们可以根据我们目前所知求解转化率和生成项。 让我们从在反应器中对 A 进行 *摩尔* 衡算开始。
) - 2 个方程(因为整体衡算已经求解!)= **1 个 DOF**。 因此,我们仍然无法完全求解反应器。 然而,我们可以根据我们目前所知求解转化率和生成项。 让我们从在反应器中对 A 进行 *摩尔* 衡算开始。

要找到三个 nA 项,我们需要将质量转换为摩尔(因为 A 是氢气 H2,分子量是  )
)


因此,进入反应器的 A 的总量为

流出的量为

因此,根据摩尔平衡,我们有以下结果


现在我们有了这个结果,就可以计算 B 和 C 的生成量


此时,您可能想要根据 B 和 C 的质量平衡来计算反应器中 B 和 C 的排出量

- (1)

然而,这些方程完全相同!因此,我们已经证明了我们的断言,即反应器中仍然存在 1 个自由度。所以我们需要在其他地方寻找东西来计算 xB5。这个地方是 B 的分离器平衡

- (2)

求解这两个方程(1)和(2)将得出系统中的最后两个变量

注意这意味着流 5 中的主要物质也是 C ( )。然而,分离器/循环设置确实产生了重大影响,正如我们将在下一节中看到的那样。
)。然而,分离器/循环设置确实产生了重大影响,正如我们将在下一节中看到的那样。
现在我们知道了从分离后的反应器中可以获得多少乙烷,让我们比较一下如果没有循环系统会发生什么。使用与本问题第一部分相同的数据,新的流程图如下所示
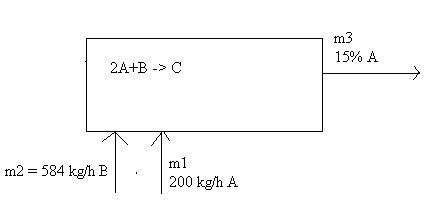
存在三个未知数 ( ) 以及三个独立的物料平衡,因此问题可以得到解决。从总物料平衡开始,因为总质量守恒
) 以及三个独立的物料平衡,因此问题可以得到解决。从总物料平衡开始,因为总质量守恒


我们可以对反应器进行与上一节相同的分析,以找出出口流中的转化率和 C 的质量百分比,这留给读者作为练习。结果是

将此与循环设置中的两个出口流进行比较。即使是排放流,两种流中的 C 的含量都比 77% 高。这是因为未反应的 A 和 B 被允许重新进入反应器并形成更多 C,分离器能够将几乎所有从未反应的 A 和 B 中形成的 C 分离出来。








































