无机化学导论/纳米材料基础科学

  纳米材料基础科学

            

彩色玻璃、防晒霜、磁性硬盘、非均相催化剂、消费电子产品、防污服装、自清洁玻璃和医疗诊断有什么共同点？它们都从纳米材料中获得了一些特殊的性能和用途：普通的元素和无机化合物，如金、银、TiO₂、铬、SiO₂和硅，当它们的特征尺寸在1 到 100 纳米之间时，会获得不同的性能。在本章中，我们将学习纳米材料的基础科学，即是什么让它们的尺寸如此不同。

第 11 章的学习目标

• 了解纳米级半导体和磁性粒子中介观行为的物理基础。
• 描述箱中粒子方程如何应用于量子阱中的电子。
• 使用 Brus 公式计算纳米级半导体粒子的带隙能量。
• 使用表面能概念计算纳米粒子的熔点和蒸气压变化。
• 描述用于制造尺寸均匀的半导体和金属纳米晶体的 方法。
• 解释金属纳米粒子中局域表面等离子体共振效应的起源。
• 描述金属纳米粒子新兴的分析和生物医学应用。

  11.1 物理和长度尺度：腔激光器、库仑阻塞、纳米磁体

纳米材料的特殊性能并非来自不同的物理定律，这些定律对于大小不同的物体都是相同的。例如，牛顿第二定律 (F = ma)、库仑定律 (E = q₁q₂/4πε₀r) 以及能量守恒和动量守恒定律对于富勒烯 (C₆₀) 和标准足球都是一样的。然而，电子的物理特性、原子和光子自然会产生特征长度尺度，我们已经见过其中的一些。例如，在第 6 章中，我们发现良好金属中电子的平均自由程约为 40 纳米。在第 10 章中，我们了解到掺杂 Si 中电子或空穴的玻尔半径约为 4 纳米，以及半导体中库珀对的相干长度在几个纳米到 1 微米之间。当物体相对于这些特征长度变小时，它们的物理特性会以有趣的方式发生变化。存在于相关长度尺度上的材料被称为介观（meso = "介于"，scopic = "大小"），这意味着它们从一种行为转变为另一种行为——大型物体的整体行为。这种长度尺度对于不同类型的特性是不同的，但对于许多特性而言，它发生在 1 到 100 纳米之间。我们用几个例子来说明这一点。

VCSEL 器件结构。这是一个底部发射多量子阱VCSEL。

腔激光器。垂直腔面发射激光器（或 VCSEL）是一种基于半导体的器件，它相对于芯片平面的方向垂直发射光。这些器件正在开发和用于高功率应用，例如激光手术、用于军事监视的红外照明以及激光切割工具。VCSEL 的基本设计如右图所示。VCSEL 本质上是一个发光二极管，包含 III-V 半导体 (Al,Ga)As 的 p 型和 n 型区域。但是，它具有两个特殊特征。首先，半导体的折射率在结点之上和之下被调制以形成布拉格反射镜。这些反射镜反射在结点中发射的光，因此光子密度在那里变得非常高，这是受激发射和激光的必要条件。布拉格反射镜堆栈是不对称的（底部更薄），因此光只能从一个方向从结点中逸出。其次，结点本身包含一层薄的“量子阱”层 (In,Ga)As，这是一种 III-V 半导体，其带隙比周围的 (Al,Ga)As 层小。

量子阱结构（其能带图如左图所示）是激光器的纳米级部分。 (Al,Ga)As 的导带和价带的能量包围着薄的 (In,Ga)As 层的能量。因此，注入到该层中的电子和空穴无法逸出： (In,Ga)As 中的电子没有足够的能量“爬上”到 (Al,Ga)As 的导带，而空穴无法“爬下”。限制在如此小阱中的电子表现得像一个箱中粒子（正如我们在第 9 章关于电化物的背景下所了解的那样）。
电子具有由以下方程定义的动能

$KE={\frac {h^{2}n^{2}}{8mL^{2}}}$

我们可以计算最低能级 (n=1) 和次低能级 (n=2) 之间的能量差，该能量差与 (In,Ga)As 层的厚度 (L) 的平方成反比。在这个计算中，我们需要使用 (In,Ga)As 中电子的有效质量，这大约是电子静止质量的 7%。对于 8 纳米厚的层，这种能量是

$E={\frac {(2^{2}-1^{2})(6.626\cdot 10^{-34}Js)^{2}}{8\cdot 0.07\cdot (9.1\cdot 10^{-31}kg)(8\cdot 10^{-9}m)^{2}}}=4.0\cdot 10^{-20}J=0.25eV$

因此，VCSEL 腔将具有 0.25 eV 的共振能量，并在红外光谱中以该能量发射光子 (λ ≈ 5000 nm)。请注意，由于腔能量与层厚度的平方成反比，因此基于这种设计的激光器只能在纳米尺寸下工作。当腔的厚度增加三倍时，其共振能量将与室温下的热能相当 (kT = 0.026 eV)，激光效应将被热能“洗掉”。

面积为 A、介电层厚度为 d 的平行板电容器的基本设计

库仑阻塞。电容器是一种（宏观）设备，用于存储电荷。电容器的基本结构如右图所示。当对这种设备施加电压时，它会在两个板上产生与电压成正比的电荷 (± Q)

$C={\frac {Q}{V}}$

电容 C 的大小由介电常数 ε 和介电层的尺寸 A 和 d 决定。

$C={\frac {\varepsilon A}{d}}$

我们还可以通过积分电压乘以电荷来计算对电容器进行充电所做的功（即充电电容器存储的能量）

单电子晶体管的示意图。

$E=\int _{0}^{Q}V(q)\mathrm {d} q=\int _{0}^{Q}{\frac {q}{C}}\mathrm {d} q={1 \over 2}{Q^{2} \over C}={1 \over 2}CV^{2}={1 \over 2}VQ$

现在有趣的是，当我们使电容器变得非常小时，会发生什么？这在一种名为单电子晶体管的设备中尤为有趣，该设备的示意图如右图所示。金属栅极引线通过一层薄介电层与一个“量子点”隔开，该量子点可以是金属或半导体粒子。这种金属-介电-金属夹层结构充当电容器，根据上面的方程式，用一个电子 (Q = e) 对其充电所需的能量是

$E={\frac {e^{2}}{2C}}$

其中 e 是电子的电荷，1.602 x 10^-19 库仑。如果栅极宽度和横向尺寸非常小，例如自组装库仑阻塞器件中可以轻松实现的 2 纳米，那么对于典型的绝缘介电材料，需要约 200 mV 的电压才能用一个电子对量子点充电。同样，这种效应是纳米尺度特有的，因为 10 倍更大的器件面积将使单电子充电电压约为 20 mV，这小于热能 kT (26 meV)。因此，对于大于约 5-6 纳米的器件，在室温下，单个电子充电事件会被热波动“洗掉”。

像这样的纳米电容器如何充当晶体管，在电路中充当开关？这种效应来自于电子的相互排斥。量子点上的一个电子会排斥任何其他想要通过施加源极和漏极之间的微小电压而被强加到它上的电子。因此，量子点的电导率在零电压的栅极偏压下非常低，或者在任何栅极偏压（200、400、600 mV...）下，这些偏压将整数个电子 (1、2、3、...) 放在量子点上。但在这些电压的中间（例如，在 100、300、500 mV 下），量子点上有 n 个电子还是 n+1 个电子，能量是相同的。这意味着电子可以在不改变能量的情况下跳上跳下，即它们可以从源极到漏极穿过量子点。这种效应在栅极电压的规则步长中使量子点的电导率出现峰值。实际上，栅极可以充当开关，就像传统的场效应晶体管一样。单电子晶体管被研究作为超灵敏的静电计和单分子化学传感器，因为量子点静电环境的微小变化会使器件开启或关闭。

纵向 和 垂直记录，两种类型的硬盘驱动器写入头。

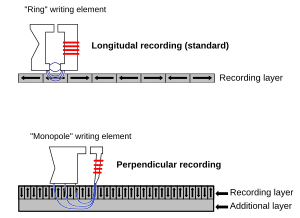
纳米磁体。铁和氧化铬等铁磁性和亚铁磁性材料用于硬盘驱动器中信息的数字化存储。单个存储位可以垂直或平行于磁盘平面排列，如右图所示，它们根据其磁偶极子的方向存储逻辑“0”或“1”。为了有用，这种信息必须是非易失性的，即磁位在没有来自读/写头的施加磁场的情况下必须保持其极化。

这种磁性存储器的存储密度令人印象深刻。一个 2.5 英寸的硬盘驱动器现在可以存储 1 TB 的信息，使用长度约为 0.5 µm 的棒状磁性颗粒。我们现在有良好的合成方法，可以将这些相同的材料作为仅几个纳米尺寸的晶体合成。为什么不使用这些纳米晶体来制作密度更高的存储磁盘呢？

包含超顺磁性 Fe₃O₄ 纳米粒子的铁磁流体，这些纳米粒子被油酸包裹并悬浮在油中，位于强永磁体的磁场中。

原因是翻转磁化所需的能量（即，将“0”变成“1”，反之亦然）与尺寸密切相关。对于铁磁体或亚铁磁体，这种能量等于 Mr³，其中 M 是单位体积的磁能，r 是磁性颗粒的特征尺寸（例如，立方体的边长或球体的直径）。对于典型的材料，如铁，当 r 约为 3-5 纳米时，这种能量变得与 kT 相当。如此小的颗粒是 超顺磁性 的，这意味着它们仍然具有很大的磁矩，因为它们的旋转有序，但在没有施加磁场的情况下，它们不会保留永久极化。因此，超顺磁性颗粒不适合用作磁性记忆，但它们在其他方面很有趣且实用，例如在 铁磁流体、磁共振成像 (MRI) 和一些新兴的医学诊断和治疗应用中。

在这三个说明性的例子（涉及光发射、电子传导和磁行为）中，向新属性的转变涉及一个交叉，其中系统的特征能量与热能 kT 相当。恰好，对于许多物理现象，这种交叉发生在纳米级的长度尺度上。

  11.2 半导体量子点

CdSe 纳米颗粒的原子分辨率图像。

不同尺寸 CdSe 纳米颗粒的发射颜色。较小的颗粒发射蓝光，因为激子能量随着尺寸减小而增加。

最令人着迷和研究最充分的中观效应之一发生在当一个或多个尺寸在几纳米范围内时，各种形状的半导体颗粒中。这些所谓的“量子点”（0D）、“量子棒”（1D）和“纳米片”（2D）获得了惊人的新电子和光学特性。

半导体量子点的合成将在下面更详细地讨论，其控制程度足以获得几千个原子的完美晶体，这在宏观晶体中是统计上不可能的。右侧显示了这种晶体的图像。在合成过程中，这些晶体可以用外延配体的层或更宽带隙半导体的壳（例如 CdSe 情况下的 ZnS）进行封端，使得内部核心有效地成为量子阱。由核心半导体激发形成的电子-空穴对被限制在那里，无法到达颗粒的外表面，否则它们可能会在那里被捕获并在热力学上复合。因此，半导体量子点的带隙发射量子产率通常很高，导致右侧所示不同尺寸 CdSe 颗粒的明亮发射颜色。由于其强烈的窄发射带，量子点作为生物成像应用的发光标签以及太阳能电池和光学显示器中的光吸收体和发射体而备受关注。半导体核-壳量子点的明亮光致发光是商业 量子点显示器 的基础，这种显示器可以比有机发光二极管 (OLED) 显示器制造出更大、更明亮的格式。

发射颜色的尺寸依赖性主要来自盒中粒子效应。当量子点吸收光时产生的电子和空穴被“盒”的限制束缚在一起，形成一个 激子。Louis Brus 使用一阶微扰理论确定半导体量子点的带隙近似为：

$E_{gap}=E_{gap,bulk}+{\frac {{h}^{2}}{8\mu {{R}^{2}}}}-{\frac {1.8{e}^{2}}{4R\pi \varepsilon {{\varepsilon }_{0}}}}+...$

其中 R 是粒子半径，µ 是电子-空穴约化质量（1/µ = 1/m_e* + 1/m_h*），m_e* 和 m_h* 是电子和空穴的 有效质量，ε 是半导体的介电常数。在这个方程中，体带隙后的第一项是由于激子限制引起的动能，第二项表示受限电子和空穴之间的静电吸引能。由于能量是 R² 的函数，因此可以通过改变量子点的尺寸在可见光谱中进行广泛调整。

  11.3 半导体纳米晶体的合成

用油酸、油酰基和羟基进行表面钝化的 5 纳米直径胶体硫化铅纳米颗粒的完整原子模型。

早期关于半导体纳米颗粒中量子尺寸效应的研究使用了简单的复分解反应来合成。例如，CdSe 和 PbS 可以通过以下反应在环境温度下沉淀出来

CdCl₂(aq) + H₂Se(g) = CdSe (s) + 2 HCl(aq)

Pb(NO₃)₂ + H₂S(g) = PbS(s) + 2 HNO₃(aq)

通过在不同的基质中进行这些反应来限制颗粒的生长，例如在聚合物薄膜或沸石的硅酸盐笼中，并且有时也使用封端配体来限制颗粒生长。虽然这些反应确实产生了纳米颗粒，但通常会获得广泛的颗粒尺寸分布。这些颗粒也不稳定，容易发生 奥斯特瓦尔德熟化 - 其中较大的颗粒以较小的颗粒为代价生长以最大限度地减少总表面能 - 因为水性介质中形成酸的合成反应的可逆性。缺乏良好的样品阻碍了详细研究和半导体量子点应用的开发。

纳米粒子合成的重要进展出现在 1990 年代初期，当时 Murray、Norris 和 Bawendi 引入了第一个用于 II-VI 半导体量子点的非水、可控生长过程。 该合成的关键是 (1) 使用非水溶剂和封端配体来稳定产品，使其免受熟化，(2) 在高温下进行反应以确保良好的结晶度，以及 (3) 将颗粒成核和生长步骤分开，从而获得尺寸均匀的颗粒。以下说明了此过程

合成是在作为三辛基膦 (TOP) 和三辛基氧化膦 (TOPO) 混合物的配位性高沸点溶剂中进行的。在早期的实验中，二乙基镉等有机金属镉化合物用作金属源，但后来发现这些剧毒和易燃化合物可以被 CdO 取代。在反应开始时，硒源，通常是二（三甲基硅基）硒，[(CH₃)₃Si]₂Se，溶解在 TOP 中，迅速注入热的（350 °C）反应混合物中。该反应导致纳米粒子快速成核，但由于注入冷溶剂，温度也会下降，因此成核事件很快结束。冷却的溶液现在包含纳米晶体种子。它在 TOPO-Cd 和 TOP-Se 中过饱和，但颗粒生长缓慢进行，直到溶液再次加热到生长温度，约为 250 °C。颗粒生长和尺寸聚焦发生是因为较小的颗粒比较大的颗粒需要更少的添加材料才能生长 ΔR。这是因为围绕球形种子的附加壳的体积为 4πR²ΔR，因此对于较大的 R，ΔR 较小。在高过饱和条件下可以获得非常窄的粒子尺寸分布，其中纳米粒子生长速度相对于粒子溶解和 奥斯特瓦尔德熟化 很快。 [6] 然后，可以通过向冷却的反应混合物中添加非溶剂，例如己烷，进一步缩小尺寸分布。最大的颗粒首先沉淀出来，然后是较小的颗粒。由于纳米颗粒被 TOP 的配体壳封端，因此在尺寸分离后，它们可以重新悬浮在有机溶剂中。

半导体量子点的**高温合成**已被应用于多种材料，包括II-VI族、III-V族和IV-VI族半导体。通过这种方法的变体可以制备出**形状可控**的单分散纳米颗粒。例如，可以通过调节条件使CdSe以闪锌矿多晶型物形式成核，形成四面体形状的种子，然后在每个三角形面上生长极性纤锌矿“臂”，形成纳米晶体四足体。通过这种技术的变体可以制备出许多其他纳米晶体形状，例如棒状、箭头状、米粒状（锥形棒状）和极性结构，例如Janus棒。这些形状控制策略通常涉及使用专门吸附在特定晶体面上并抑制其生长的配体。例如，己基膦酸配体选择性地吸附在富Cd晶体面上，从而导致棱柱形纤锌矿相CdSe纳米晶体的生长。

以金纳米粒子为催化剂，在气-液-固（VLS）工艺中外延生长硅纳米线。

另一种广泛使用的半导体纳米晶体合成方法涉及从分子前驱体和熔融金属液滴中生长，如图右侧所示。**气-液-固（VLS）**和相关的**溶液-液-固（SLS）**生长过程依赖于这样一个事实，即硅、锗、砷化镓、磷化铟等半导体在高温下可溶于金和铜等液态金属。例如，四氯化硅（SiCl₄）在金纳米晶体表面的催化还原反应释放出氯化氢气体，并在金中形成硅的固溶体。硅的存在降低了金的熔点，随着更多四氯化硅的反应，形成了硅-金合金的液态**共晶**液滴。当该液滴中硅的含量过饱和时，硅纳米晶体就会成核并生长。该反应可以在宏观硅晶体的表面进行，在这种情况下，纳米晶体“晶须”从表面生长，通常为单晶，并且外延取向由基底的硅晶体面决定。晶须的直径由金液滴的半径控制，金液滴的半径可以小到几纳米，也可以大到几微米。使用这种技术，可以生长出纳米线或微线的“森林”。由于纳米线的组成取决于供应到金液滴的前驱体，因此可以沿纳米线轴制备出具有不同组成的“图腾柱”结构。还可以通过**化学气相沉积（CVD）**在纳米线周围生长半导体外壳。VLS工艺还可以通过使用激光从固体靶材中烧蚀半导体来适应没有分子前驱体的复杂成分。

通过这种方法制备的半导体纳米线是极其灵敏的**生物传感器**的基础，在这种生物传感器中，纳米线上的任何分子结合事件都会强烈影响其电导率。 纳米线和微线阵列也被研究用作**太阳能电池**组件，并作为**锂电池**材料被商业化生产，以及纳米级热电、电子和光电器件。

  11.4 表面能

如图右侧所示，纳米粒子有很大一部分原子位于表面。 这种高表面积与体积比是许多纳米粒子物理性质的重要因素，例如它们的**熔点**和**蒸气压**，以及它们的**反应性**。例如，非均相催化剂通常基于纳米粒子，因为催化活性原子是位于粒子表面的原子。

**表面能始终为正值。**与所有表面化学相关的关键量是**表面能**。这是形成表面“悬空键”的（热力学上不利的）能量。表面原子配位不足，由于断裂键需要能量，因此表面原子总是比体相原子具有更高的能量。无论键合是共价键（如金属）、离子键（如盐）还是非共价键（如水等液体），都会发生这种情况。例如，我们在蜡表面上的水滴呈珠状时看到了这种效应。水滴收缩成球形（抵消了使水滴变平的重力），以最大限度地减少表面悬空的氢键数量。

在金属或半导体颗粒的情况下，表面会断裂强共价键。例如，体相面心立方金中的金原子具有 12 个最近邻，但晶体（111）表面（金最密集的晶体面）上的金原子在平面内具有 6 个最近邻，在下方具有 3 个最近邻，总共 9 个。我们可以预计该晶体面的表面能会略微降低（因为剩余的键会变得稍微更强），约为体相金的 3/12 = **1/4 的键合能**，而这实际上是许多材料的相当好的经验法则。当换算为每单位面积的能量时，金属和无机盐的表面能通常在 1-2 J/m² 范围内。

**示例：** 体相金的升华能为 334 kJ/mol，表面能为 1.5 J/m²。金晶体（111）表面上的原子损失了体相键能的百分比是多少？

要解决这个问题，我们需要知道每个金原子的表面积。金具有面心立方结构，晶胞边长为 4.08 Å。由此我们可以确定 Au-Au 距离为 4.08/1.414 = 2.88 Å。在具有此原子间距的金原子六方排列中，每个原子的表面积为 (2.88 Å)² x 0.866 = 7.2 Ų。乘以阿伏加德罗常数，我们发现（111）晶体面上每摩尔金表面原子的面积为 **4.3 x 10⁴ m²。**

现在我们将此面积乘以表面能

(4.3 x 10⁴ m²/mol) x (1.5 J/mol) x (1 kJ/1000 J) = **+65 kJ** 每摩尔金表面原子。

65 kJ/334 kJ x 100% = **19%** 的体相键能被表面原子损失了。

从这个例子可以清楚地看出，纳米粒子的表面能会对其物理性质产生重大影响，因为纳米粒子中很大一部分原子位于表面。**熔点**急剧下降就是一个很好的例子。

固体纳米晶体通常是多面的，而通过熔化纳米晶体形成的液滴则采用球形形状以最小化表面积。

为了最小化表面能，多面体固体纳米晶体熔化成球形液滴。

让我们考虑熔化直径为 2 nm 的银纳米晶体，这意味着大约 1/2 的原子位于表面。球形液滴的表面积比多面体晶体低。例如，立方体的表面积是相同体积的球体的 1.24 倍。如果熔化时的表面积减少约 20%，并且表面能约为体相原子键合能的 1/4，那么对于直径为 2 nm 的纳米晶体，我们估计

ΔH°_熔化 ≈ ΔH°_{熔化，体相} - (1/2)(0.25)(1/4)ΔH°_汽化 = ΔH°_{熔化，体相} - 0.025 ΔH°_{汽化，体相}

其中 ΔH°_{汽化，体相}，即汽化热，是体相晶体中原子的总键能。对于银，ΔH°_{熔化，体相} = 11.3 kJ/mol 且 ΔH°_{汽化，体相} = 250 kJ/mol。由此我们可以计算出直径为 2 nm 的 Ag 纳米晶体的熔化热

ΔH°_熔化 ≈ 11.3 - (0.025)(250) = 5.1 kJ/mol

体相银的熔点为 962 °C = 1235 K。假设熔化熵在体相和纳米晶体中相同，则纳米晶体的熔点应为 1235 K x (5.1/11.3) = 557 K = 284 °C，与体相值相比下降了近 700 度。实验表明，直径为 2 nm 的银纳米晶体的熔点下降了约 **800 度**，降至 127 °C。 这是一个巨大的熔点变化，与我们的粗略估计大体一致。

相同的效应——表面原子相对于体相原子的能量不稳定——导致纳米晶体相对于相同材料的微晶体（或更大晶体）具有**较低的沸点**、**较高的蒸气压**、**较高的溶解度**和**较高的反应性**。

  11.5 纳米级金属粒子

金纳米粒子中的五重孪晶

在过去的 20 年里，纳米级金属粒子一直是研究的热点，尤其是它们独特的**光学**、**磁性**和**催化**特性。各种形状的金属纳米晶体的合成变得越来越复杂和合理，就像上面描述的半导体纳米晶体的合成一样。通过控制成核和生长的各个阶段，并使用在生长过程中封端特定晶体面的配体，可以制备出各种有趣且有用的形状的尺寸均匀的金属纳米晶体，包括立方体、截角立方体、八面体、三角棱柱和高长径比棒状。通过利用将一种金属替换为另一种金属的置换反应，可以从其他形状开始制备出复杂的空心形状，例如纳米笼（如左侧所示）。在这种情况下，固体银纳米立方体被转化为金纳米笼。

利库尔格斯杯（公元四世纪的罗马玻璃制品）独特的颜色来自于贵金属纳米颗粒。在透射光下，杯子呈现红色，而在散射（反射）光下呈现绿色。

纳米晶体金、银、铜和其他一些金属的有趣的光学特性，源于它们价电子的集体振荡，这种现象被称为等离子体共振。请记住，在这些金属中，电子平均自由程很长（大约是原子大小的 100 倍），因此价电子在晶体中快速移动时，只感受到原子核的平均正电荷。照射到金属上的光表现为振荡电场，以光的波长特征频率推拉价电子。这种情况非常类似于摆锤或弹簧上的重物。电子被推离平衡位置，会感受到一个与其位移成正比的恢复力。它们的运动可以用胡克定律来描述

F = kx

其中弹簧常数 k 决定了弹簧的“刚度”。在等离子体共振的情况下，k 与价电子数密度 n 和电子电荷 e 的平方成正比

k = ne²/ε₀

等离子体振荡的共振频率由下式给出

ω_p = (k/m)^1/2 = (ne²/m_eε₀)^1/2

其中 m_e 是电子质量。对于大多数金属，等离子体共振位于光谱的紫外部分，但对于一些金属如金、银和铜，它位于可见光部分。

等离子体金纳米颗粒的颜色取决于它们的大小和形状。

对于远小于光波长的金属颗粒，这种效应被称为局域表面等离子体共振，或 LSPR。LSPR 效应有三个重要结果

• 入射光波的局部电场在颗粒表面显著增强。这导致光学过程（如拉曼散射和荧光）产生巨大的增强因子。因此，某些分析光谱技术通过 LSPR 显著增强。
• 在等离子体共振频率附近，金属纳米晶体强烈地吸收和散射光。这使得它们具有明亮的反射性，强烈的光吸收可用于光诱导的局部加热。这些性质正在应用于医疗诊断和治疗，例如用于检测和光热破坏癌细胞。通过调整金纳米颗粒的大小和形状，这些纳米颗粒在生物介质中比银和铜更稳定，等离子体频率可以调谐到组织透明的近红外区域（700 到 900 纳米）。少量等离子体银和金颗粒也能形成颜色鲜艳且散射性强的颜料，例如上图右侧所示的彩色玻璃。
• 等离子体频率对颗粒周围介质的折射率（即其化学环境）敏感。这使得金属纳米颗粒在传感和生物传感应用中具有特殊意义。

金属纳米颗粒散射和吸收光的理论。金属纳米颗粒中的价电子在光波的电场中振荡。虽然这些振荡的本质在非球形金属颗粒中比较复杂，但球形颗粒的理论相对简单，事实上，它在一百多年前就被德国物理学家古斯塔夫·米推导出来。

米考虑了一个球形颗粒与均匀电场 E 的相互作用，该电场以角频率 ω（= 2πf）振荡。当颗粒直径远小于光波长时，这是一个很好的近似，如左侧所示。该颗粒嵌入均匀的绝缘材料（例如溶剂）中，该材料具有介电常数 ε_diel。对于绝缘体，ε_diel 是一个正实数。

金属的介电常数 ε 实际上是一个复数

$\epsilon =\epsilon '+i\epsilon ''$

这里，实部 ε' 与光的折射有关，虚部 ε'' 与光的吸收有关。ε' 和 ε'' 都依赖于光的频率。对于等离子体共振频率附近的金属，ε' 通常是一个负数。

光波被颗粒吸收的截面是

${\sigma _{absorption}}={\frac {9\omega }{c}}\epsilon _{diel}^{3/2}V{\frac {\epsilon _{metal}''}{(\epsilon _{metal}'+2\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}}$

光波被颗粒散射的截面是

${\sigma _{scattering}}={\frac {3}{2\pi }}({\frac {\omega ^{4}}{c}})\epsilon _{diel}^{2}V^{2}{\frac {(\epsilon _{metal}'-\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}{(\epsilon _{metal}'+2\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}}$

这两个的总和是消光截面

${\sigma _{extinction}}={\sigma _{absorption}}+{\sigma _{scattering}}$

当分母中的 (ε'_metal + 2ε_diel) 项变小时，这些截面会变大。这种情况发生在

$\epsilon _{metal}'\simeq -2\epsilon _{diel}$

对于水中直径为 15 纳米的金纳米颗粒，这种情况发生在大约 580 纳米处，导致胶体金溶液呈现出特征性的酒红色。改变溶液环境（例如，通过吸附分子到金表面）会改变ε_diel，从而略微改变颜色。

需要注意的是，散射的截面与颗粒的体积平方（V²）成正比，而吸收与 V 成正比。这意味着非常小的金颗粒（< 5 纳米）具有很强的吸收性，但散射性不强。较大的颗粒（>30 纳米）散射光非常强。因此，根据应用的不同，我们选择较大和较小的颗粒。

贵金属纳米颗粒的一个关键互补特性是它们可以很容易地与聚合物或小分子共价偶联，这对于它们在生物医学中的应用非常重要，通常通过其表面的硫醇或胺键。这赋予颗粒生物识别特性，使其能够与特定的生物分子靶标结合。左侧的图说明了通过表面功能化可以赋予纳米颗粒的一些功能。

金纳米颗粒的聚集（在本例中通过向胶体溶液中添加盐）导致颜色从酒红色（左）变为蓝色（右）。照片来源：威斯康星州立大学比洛伊特分校的乔治·利辛斯基

用硫醇封端的单链 DNA 对金纳米颗粒进行功能化是第一个纳米颗粒传感器的基础，该传感器由西北大学的米尔金小组开发。DNA 包覆的纳米颗粒具有球形纳米金的特征性酒红色等离子体颜色。然而，当这些颗粒通过互补 DNA 链连接在一起时，共振频率会发生偏移，导致蓝色。这种颜色变化如右侧图所示，为目标 DNA 序列的存在提供了一个“试纸”。 DNA 的“熔化”——将其加热到双链 DNA 解离形成单链的温度——会逆转颜色变化。由于许多金颗粒的聚集，DNA 杂交/熔化转变具有高度的协同性，因此转变温度非常尖锐。通过适当的温度控制，颜色变化可以对这种方法检测到的目标 DNA 中的单个碱基错配敏感。

基于纳米耀斑检测的通用示意图。

随后的研究已经开发出针对这些球形核酸颗粒的复杂诊断和治疗（“治疗诊断”）应用。这些颗粒很容易穿透细胞膜，并可以报告活细胞内部发生的化学反应。

金纳米颗粒在这些应用中的一个重要特性是它们能够猝灭其表面附近报告分子发出的荧光。含有发夹环的核酸链可以将荧光分子定位在金表面附近，在那里它们的荧光会被纳米颗粒猝灭。这些序列与目标 RNA 或 DNA 的杂交会导致荧光分子远离纳米颗粒表面，从而使荧光重新开启。因此，这些所谓的“纳米耀斑”可以发出特定基因在细胞内上调或下调的信号。纳米耀斑是维尔金系统（由 Nanosphere，Inc. 开发并商业化）的基础，用于检测传染病和癌症的标志物。

  11.6 纳米材料的应用

本节的 PowerPoint 幻灯片

  11.7 讨论问题

• 解释分离成核和生长步骤是如何导致尺寸均匀的纳米颗粒的。
• Delia Milliron 及其同事最近发表的一篇论文（Nature，2013，500，323–326，doi:10.1038/nature12398）描述了能够控制窗户红外透明度的等离子体氧化铟锡（ITO）纳米颗粒。解释纳米颗粒的等离子体共振波长如何可以通过电化学掺杂来调节，以及这项发明如何可以节省用于加热和冷却建筑物的一些能源。

  11.8 问题

1. 考虑一个包含 500 个原子的球形金纳米颗粒。如果一个原子的直径大约为 3 Å，那么颗粒中位于表面的金原子所占比例是多少？

2. 现在考虑包含 500 个原子的汞小液滴。汞原子直径也约为 3 Å。块状汞的汽化热为 64.0 kJ/mol，汞的蒸气压为 0.00185 托 = 2.43 x 10^-6 atm。汞的表面张力（γ_Hg）为 0.518 N/m，表面过剩能量可以计算为 γ_HgA，其中 A 为表面积。利用这些信息和克劳修斯-克拉佩龙方程（P = const•exp(-ΔH_vap/RT)），计算这些汞小液滴的蒸气压。

3. James Heath 及其同事（Phys. Rev. Lett. 1995, 75, 3466）在室温下观察到金纳米颗粒薄膜中的奥斯特瓦尔德熟化现象。从不均匀的粒径分布开始，他们发现大颗粒以牺牲小颗粒为代价而生长。根据你对问题 (1) 和 (2) 的答案，你能解释这种现象吗？

4. 块状锗的带隙为 0.67 eV。你预计直径为 4 纳米的锗纳米晶体会有多少带隙？使用布鲁斯公式，

$\Delta {{E}_{gap}}\approx {\frac {{h}^{2}}{8\mu {{R}^{2}}}}-{\frac {1.8{e}^{2}}{4R\pi \varepsilon {{\varepsilon }_{0}}}}+...$

其中 R 为粒子半径，ε_Ge = 16.2，h = 6.6 10^-34 J s，1 eV = 1.6 10^-19 J，1 J = 1 kg m²/s²。以及 e²/4πε₀ = 1.44 10^-9 eV m。假设电子-空穴约化质量 μ 约为自由电子质量的 40%，m_e = 9.1 10^-31 kg。

5. 希腊配方（一种染发产品）直到最近还含有醋酸铅，醋酸铅与头发中的半胱氨酸反应生成 PbS。块状 PbS 是一种带隙为 0.3 eV（1 eV = 1240 纳米）的半导体。这些颗粒最初非常小，但随着更多希腊配方被使用并与半胱氨酸反应，它们会逐渐长大。随着颗粒的生长，它们的颜色会从无色逐渐变为黄色，最后变为黑色。解释为什么这些颗粒最初是无色的以及为什么它们的颜色会发生变化。（希腊配方现在使用 Bi，Bi 的毒性低于 Pb，并且通过相同的机制起作用）