无机化学/配位化学与晶体场理论导论

配位化合物(或配合物)是包含过渡金属离子与一个或多个配体之间键的分子和扩展固体。在形成这些配位共价键时,金属离子充当路易斯酸,配体充当路易斯碱。通常,配体具有孤对电子,并且键的形成是通过包含此电子对的分子轨道与金属离子的d轨道重叠而形成的。在配位配合物中常见的配体是中性分子(H2O、NH3、吡啶等有机碱、CO、NO、H2、乙烯和膦PR3)和阴离子(卤化物、CN-、SCN-、环戊二烯(C5H5-)、H-等)。所得配合物可以是阳离子(例如,[Cu(NH3)4]2+)、中性([Pt(NH3)2Cl2])或阴离子([Fe(CN)6]4-)。正如我们将在下面看到的,作为布朗斯台德碱具有弱或可忽略不计强度的配体(例如,CO、CN-、H2O和Cl-)仍然可以在形成过渡金属配合物中成为有效的路易斯碱。
对于作为路易斯碱的配体,配位共价键(也称为配位键)通常被画成线,或者有时用箭头表示电子对“属于”配体X。

在计算金属上的电子(如下所述)时,惯例是将配位键中的两个电子都分配给配体,尽管实际上键通常是极性共价键,并且电子在金属和配体之间共享。
在写出配位化合物的分子式时,我们使用方括号[...]括起来直接键合在一起的金属离子和配体。因此,化合物[Co(NH3)5Cl]Cl2包含八面体[Co(NH3)5Cl]2+离子,其中五个氨分子和一个氯离子直接键合到金属上,以及两个未与金属配位的Cl-阴离子。



历史。配位化合物已经存在了几个世纪,但最初人们并不了解它们的结构。例如,普鲁士蓝,其经验式为Fe7(CN)18•xH2O,是一种不溶性的深蓝色固体,自1704年迪斯巴赫偶然发现以来一直用作颜料。普鲁士蓝实际上包含Fe3+阳离子和[Fe(CN)6]4-阴离子,更具描述性的表述为(Fe3+)4([Fe(CN)6]4-)3•xH2O。像Co3+的氨配合物这样的简单化合物是化学家所熟知的,但它们不符合离子固体的预期行为。例如,氯化钴(III)六氨,[Co(NH3)6]Cl3被配制为CoCl3•6NH3。它具有神秘的特性,因为它像离子固体一样溶于水中,但在重结晶时保留了六个氨分子。更有趣的是,观察到过渡金属配合物(如[Co(NH3)4Cl2]Cl)可以制成化学上不同的形式(异构体)。这个难题由阿尔弗雷德·维尔纳解决,他于1893年提出这些Co配合物包含八面体配位的金属离子,这些金属离子与六个配体形成主要(共价)键。维尔纳通过电导率测量表明,CoCl3•6NH3溶液每摩尔含有三个游离Cl-阴离子和一个[Co(NH3)6]3+阳离子。后来的磁化率测量证实了盐及其溶液中都存在抗磁性Co3+。维尔纳的理论也解释了[Co(NH3)4Cl2]+存在两种(且仅两种)结构异构体的原因。
像有机化合物一样,过渡金属配合物的大小、形状、电荷和稳定性可以有很大的差异。我们将看到由金属的d轨道形成的键在很大程度上控制了这些性质。
第5章的学习目标
- 确定配合物中过渡金属的氧化态并分配d电子数。
- 推导出八面体、拉长的八面体、四方锥体、平面正方形和四面体配合物的d轨道分裂模式。
- 对于八面体和四面体配合物,确定未成对电子的数量并计算晶体场稳定化能。
- 了解分光化学序列,解释不同类型的配体如何影响晶体场分裂能,并用它来预测高自旋与低自旋配合物以及过渡金属配合物的颜色。
- 利用过渡金属配合物的磁矩确定其自旋状态。
- 了解Jahn-Teller效应的起源及其对配合物形状、颜色和反应性的影响。
- 了解螯合和环状配体形成的配合物的额外稳定性。
d轨道是过渡金属配合物的边界轨道(HOMO和LUMO)。配合物的许多重要性质——其形状、颜色、磁性和反应性——取决于金属d轨道的电子占据情况。为了理解和解释这些性质,了解如何计算d电子非常重要。
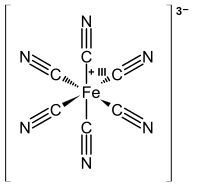
因为过渡金属通常比形成金属-配体键的配体上的原子(C、N、O、Cl、P...)电负性更低,所以我们的惯例是将键中的两个电子都分配给配体。例如,在铁氰根配合物[Fe(CN)6]3-中,如果氰化物配体保留了它的两个电子,则将其配制为CN-。通过差值,铁必须是Fe3+,因为电荷(3+ + 6(1-))必须加起来等于配合物的总电荷-3。
下一步是确定Fe3+离子有多少个d电子。规则是将铁的所有价电子都算作d电子。铁位于第8族,因此
- 第8族 - 3+电荷 = d5(或3d5)
- 8 - 3 = 5
同样的过程可以应用于任何过渡金属配合物。例如,考虑配合物[Cu(NH3)4]2+。由于氨是中性配体,因此Cu处于2+氧化态。铜(II)位于元素周期表第11族,其价电子层中有11个电子,减去2,剩下9个d电子(3d9)。在中性配合物[Rh(OH)3(H2O)3]中,Rh处于+3氧化态,位于第9族,因此电子数为4d6。第12族的锌(II)在[Zn(NH3)4]2+中将有10个d电子,形成一个完整的电子层,而锰(VII)在MnO4-中则没有d电子。镍羰基Ni(CO)4含有中性CO配体和处于零氧化态的Ni。由于Ni位于第10族,我们将Ni上的电子数记为3d10。
关于电子计数的一个常见困惑是金属上s电子的去向。例如,我们的电子计数规则预测Ti在八面体配合物[Ti(H2O)6]3+中为3d1。但根据构造原理,自由Ti原子的电子构型为4s23d2。为什么Ti3+离子是3d1而不是4s1?同样,为什么我们将Mn2+分配为3d5而不是4s23d3?简而言之,是因为在金属配合物中,金属s轨道的能量高于自由原子中的能量,因为它们具有反键特性。我们将在第5.2节中使用分子轨道图来证明这一说法。
共价键分类(CBC)方法。尽管我们上面开发的电子计数规则很有用,并且适用于所有类型的配合物,但将配合物中所有共享电子分配给配体的做法并不总是代表真实的键合图像。这种图像在配体电负性远大于金属的情况下最为准确。但实际上,存在各种各样的配体,包括H、烷基、环戊二烯基等,其中金属和配体的电负性相当。在这些情况下,特别是对于电负性相对较高的后过渡金属,我们应该将金属-配体键视为共价键。CBC方法,也称为LXZ符号,由M. L. H. Green[2]于1995年提出,以便更好地描述不同类型的金属-配体键。下面的分子轨道图总结了L、X和Z配体之间的区别。[3]其中,L和X是最常见的类型。

L型配体是路易斯碱,无论使用何种电子计数方法,都会向金属中心贡献两个电子。这些电子可以来自孤对电子、π或σ供体。这些配体与金属之间形成的键是配位共价键,也称为配位键。此类配体的例子包括CO、PR3、NH3、H2O、卡宾(=CRR')和烯烃。


X型配体是指在使用中性配体电子计数法时,向金属贡献一个电子并从金属接受一个电子,或者在使用供体对电子计数法时,向金属贡献两个电子的配体。[4]无论将其视为中性还是阴离子,这些配体都会产生正常的共价键。此类配体的一些例子包括H、CH3、卤素和NO(弯曲)。
Z型配体是指从金属中心接受两个电子,而不是像其他两种类型的配体那样进行供体。然而,这些配体也像L型一样形成配位共价键。这种类型的配体通常不使用,因为在某些情况下它可以用L和X表示。例如,如果Z配体伴随着L型,它可以写成X2。这些配体的例子包括路易斯酸,例如BR3。
一些多齿配体可以作为配体类型的组合。一个著名的例子是环戊二烯基(或Cp)配体,C5H5。我们将这种中性配体分类为[L2X],其中两个L官能团对应于两个“烯烃”片段,而X官能团对应于环中CH“自由基”碳。添加一个电子会生成Cp-阴离子,它具有六个π电子,因此是平面的和芳香性的。在二茂铁配合物Cp2Fe中,使用“标准”供体对计数方法,我们可以将两个Cp-配体分别视为具有六个π电子,根据差值,Fe处于+2氧化态。Fe2+离子为d6。因此,配合物中的铁原子(无论使用何种计数方法)在其配位环境中都有6+6+6=18个电子,对于过渡金属配合物来说,这是一个特别稳定的电子数。
晶体场理论是解释过渡金属配合物的结构和性质的最简单的模型之一。该理论基于金属-配体相互作用的静电学,因此,当金属-配体键基本上是共价键时,其结果仅是近似的。但由于该模型有效地利用了分子对称性,因此在描述金属配合物的磁性、颜色、结构和相对稳定性方面,它可以出奇地准确。
考虑一个带正电的金属离子,例如“场”中六个带负电的配体(例如CN-)中的Fe3+。我们需要考虑两个能量项。第一个是金属和配体之间的静电吸引,它与它们之间的距离成反比
第二个项是当第三个电子添加到填充轨道时,由泡利不相容原理产生的排斥。除了进入更高能量的反键轨道外,这个第三个电子无处可去。当配体孤对电子接近占据的金属d轨道时,就会出现这种情况

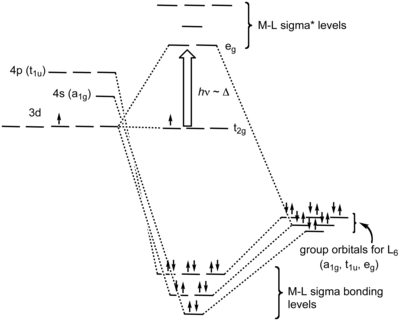
现在让我们考虑当金属离子与配体结合在一起时,这些吸引力和排斥项的影响。我们分两步进行:首先在金属周围形成一个配体“球”,然后将六个配体移动到八面体的顶点。最初,所有五个d轨道都是简并的,即由于对称性,它们具有相同的能量。在第一步中,反键相互作用使轨道的能量升高,但它们仍然是简并的。在第二步中,d轨道分裂成两个对称性类别,一个较低能量的三重简并组(t2g轨道)和一个较高能量的二重简并组(eg轨道)。
eg和t2g轨道之间的能量差用符号ΔO表示,其中“O”代表“八面体”。我们将看到,这种分裂能对轨道重叠的程度敏感,因此取决于金属和配体。相对于中点能量(重心),t2g轨道被稳定了2/5 ΔO,而eg轨道在八面体配合物中被不稳定了3/5 ΔO。

是什么导致d轨道分裂成两组?回想一下,d轨道相对于笛卡尔坐标轴具有特定的取向。dxy、dxz和dyz轨道的叶瓣(t2g轨道)分别位于xy-、xz-和yz-平面。这三个d轨道在x-、y-和z-方向上具有节点。包含配体孤对电子的轨道沿这些轴取向,因此与金属t2g轨道没有重叠。很容易看出,这三个d轨道必须通过对称性是简并的。另一方面,dz2和dx2-y2轨道的叶瓣(eg轨道)直接指向键合轴,并与配体轨道有很强的重叠。虽然不太直观,但这些轨道也通过对称性是简并的,并且具有反键特性。
比较晶体场理论和分子轨道理论(在此上下文中也称为配体场理论)对于八面体过渡金属配合物的结果是有益的。下面的能级图对d1八面体离子[Ti(H2O)6]3+进行了比较。在右侧的MO图中,前沿轨道来自金属d轨道。较低的t2g组包含一个电子,由于对称性是非键合的,而eg轨道是反键合的。金属4s轨道具有a1g对称性,形成一个配体中心的低能键合组合,以及一个金属中心的、高于eg能级的反键合组合。这就是为什么我们的d电子计数规则不需要考虑金属4s轨道的原因。重要的收获信息是,对于过渡金属配合物的前沿轨道,晶体场理论和MO理论给出了非常相似的结果。


强场配体和弱场配体。分光化学序列根据其八面体配合物中t2g和eg轨道之间的能量差ΔO对配体进行排序。此能量差通过这些能级之间的光谱跃迁来测量,该跃迁通常位于光谱的可见光部分,并导致具有部分填充d轨道的配合物的颜色。产生较大分裂的配体称为强场配体,而产生较小分裂的配体称为弱场配体。
简化的分光化学序列为
弱场 I- < Br- < Cl- < NO3- < F- < OH- < H2O < 吡啶 < NH3 < NO2- < CN- < CO 强场


轨道重叠。参考上面的分子轨道图,我们看到d电子能级之间的分裂反映了eg金属轨道与配体之间的反键相互作用。因此,我们预计配体场强度与金属-配体轨道重叠相关。通过非常电负性的原子(例如O和卤素)键合的配体预计为弱场,而通过C或P键合的配体通常为强场。通过N键合的配体强度中等。换句话说,硬碱倾向于成为弱场配体,软碱是强场配体。
- 能量单位。能量可以通过多种方式计算,并且尝试将分裂能ΔO与键能等更熟悉的量联系起来非常有用。
- 当ΔO通过光学测量时,一个波长为λ的光子被吸收,电子从t2g轨道跃迁到eg轨道。光子能量与其波长和频率的关系为
- E = hν = hc/λ = hc
- 这里ν是电磁辐射的频率,h是普朗克常数(6.626x10-34 J*s),c是光速。称为“波数”,是波长的倒数,通常以cm-1为单位。光谱学家通常用波数表示能隙。
- 例如,红光子的波长约为620 nm,波数约为16,000 cm-1。用其他能量单位表示,相同的红光子的能量为2.0 eV(1 eV = 1240 nm)或193 kJ/mol(1 eV = 96.5 kJ/mol)。如果我们将其与碳-碳单键的解离能(350 kJ/mol)进行比较,我们会发现C-C键的能量约为红光子的两倍。我们需要紫外光子(E > 350 kJ/mol = 3.6 eV = 345 nm = 29,000cm-1)才能断裂C-C键。
我们将看到ΔO在过渡金属配合物中变化很大,从近红外到紫外波长。因此,t2g和eg轨道之间的能量差可以在相当弱的共价键到相当强的共价键的能量之间变化。
ΔO取决于金属和配体。我们可以通过比较一系列d6金属配合物来了解ΔO的趋势
配合物 ΔO (cm-1) [Co(H2O)6]2+ 9,300 [Co(H2O)6]3+ 18,200 [Co(CN)6]3- 33,500 [Rh(H2O)6]3+ 27,000 [Rh(CN)6]3- 45,500
ΔO的重要趋势:
- 具有相同配体的Co3+配合物的ΔO大于Co2+配合物。这反映了晶体场分裂的静电性质。
- Rh3+配合物的ΔO大于Co3+配合物。一般来说,第二和第三过渡系元素(4d和5d元素)的分裂更大,而不是3d系元素。
- 对于一种氧化态的给定金属(例如,Co3+),ΔO的趋势遵循分光化学序列。因此,含有强场配体CN-的[Co(CN)6]3-的ΔO大于含有弱场配体H2O的[Co(H2O)6]3+的ΔO。

4d和5d元素的尺寸和化学性质相似。在比较3d、4d和5d系配合物的ΔO值时(例如,比较Co、Rh、Ir或Fe、Ru、Os三元组中的元素),我们总是发现3d << 4d ≲ 5d。这种趋势反映了d轨道的空间范围,以及它们与配体轨道的重叠。3d轨道较小,并且它们在成键方面不如4d或5d有效。由于镧系收缩,4d和5d轨道彼此相似。在5d系的开始(56Ba和72Hf之间)是14个镧系元素(57La - 71Lu)。
尽管5d元素的价轨道处于比4d元素更高的主量子层,但在穿过镧系元素的过程中,原子核增加了14个质子,导致原子轨道的尺寸收缩。重要的结果是,4d和5d元素的价轨道具有相似的尺寸,因此这些元素在化学性质上的相似性远大于它们与3d系中的同族元素的相似性。例如,Ru的化学性质与Os非常相似,如右侧所示,但与Fe的化学性质大不相同。
过渡金属配合物的颜色。观察过渡金属配合物的颜色是一种简单、定性的方法来了解相对的晶体场分裂能ΔO。吸收的光子能量越高,能隙越大。然而,配合物吸收的颜色与其呈现的颜色(即它反射的光的颜色)互补,在色轮上与吸收的颜色相反。
示例:(所有d7 Co2+配合物)
[Co(H2O)6]2+在其盐和浓溶液中呈现紫色,因为它吸收绿色范围的光。
[Co(NH3)6]2+呈稻草色,因为它吸收蓝色范围的光。
[Co(CN)6]4-呈红色,吸收光谱的紫外和紫外部分。这与CN-是比NH3更强的场配体的观点一致,因为UV光子的能量高于红橙光子的能量。
此方法适用于大多数过渡金属配合物,因为它们中的大多数都吸收可见光范围(400-700 nm = 25,000到14,300 cm-1)中的某个波长,或者具有延伸到可见光的紫外跃迁,使它们看起来呈黄色;然而,也有一些配合物,如[Rh(CN)6]3-,因为它们的d-d跃迁位于紫外区域,所以看起来无色。其他配合物,如[Mn(H2O)]62+,颜色较浅,因为它们的d-d跃迁涉及配合物自旋状态的变化。

导致CO、CN-和膦等配体具有高配体场强的一个重要因素是金属与配体之间的π键。金属配合物中存在三种类型的π键

最常见的情况是,当像一氧化碳或氰化物这样的配体将其σ(非键合)电子给予金属,同时通过金属t2g轨道和配体π*轨道之间的重叠从金属接受电子密度时。这种情况称为“反键”,因为配体将σ电子密度给予金属,而金属将π电子密度给予配体。因此,配体充当σ-给体和π-受体。在π反键中,金属将π电子给予配体π*轨道,在反键分子轨道中增加电子密度。这导致C-O键减弱,这在实验上观察到为键的伸长(相对于气相中的自由CO)和C-O红外伸缩频率的降低。
d-d π 键发生在诸如磷之类的元素与金属键合时,磷具有σ对称的孤对电子和一个空的3d轨道,而金属则在t2g轨道中具有电子。对于与低价晚过渡金属键合的膦配合物(例如,三苯基膦),这种情况很常见。在这种情况下,反键合类似于CO的例子,只是受体轨道是磷的3d轨道而不是配体的π*轨道。这里,膦配体充当σ-给体和π-受体,形成dπ-dπ键。
第三种金属-配体π键发生在π-给体配体(一种既具有σ对称电子对又具有填充的正交p轨道的元素)与金属键合时,如上图右侧所示,例如O2-配体。这发生在早期过渡金属配合物中。在这个例子中,O2-同时充当σ-给体和π-给体。这种相互作用通常被描绘成金属-配体多重键,例如,氧钒阳离子[VO]2+中的V=O键。典型的π-给体配体有氧化物(O2-)、氮化物(N3-)、酰胺(RN2-)、醇盐(RO-)、酰胺(R2N-)和氟化物(F-)。对于晚过渡金属,强π-给体与填充的d能级形成反键相互作用,这对自旋态、氧化还原电位和配体交换速率产生影响。π-给体配体在光谱化学序列中位置较低。[5]


含碳的π-给体配体及其与过渡金属离子的配合物在烯烃复分解反应中非常重要,该反应中碳-碳双键发生交换。使用这些催化剂,环状烯烃可以通过开环复分解聚合(ROMP)高产率地转化为线性聚合物。这种类型的催化剂是由Richard Schrock和Robert Grubbs的研究小组开发的,他们与Yves Chauvin共同获得了2005年诺贝尔化学奖,以表彰他们的发现。Schrock催化剂基于早期过渡金属如Mo;它们反应性更强,但对不同的有机官能团和质子溶剂的耐受性不如Grubbs催化剂,后者基于Ru配合物。
过渡金属配合物中d轨道分裂成不同能级的现象对其稳定性、反应性和磁性具有重要影响。让我们首先考虑八面体配合物[M(H2O)6]3+的简单情况,其中M = Ti、V、Cr。由于配合物是八面体,它们都具有相同的能级图。

Ti3+、V3+和Cr3+配合物分别具有一个、两个和三个d电子,它们分别填充简并的t2g轨道。根据洪特规则,自旋平行排列,洪特规则指出,最低能量状态具有最高的自旋角动量。
对于每个配合物,我们都可以计算一个晶体场稳定化能,CFSE,它是配合物处于基态与处于所有五个d轨道都处于能量重心处的假设状态之间的能量差。
- 对于Ti3+,有一个电子被稳定了2/5 ΔO,所以CFSE = -(1)(2/5)(ΔO) = -2/5 ΔO。
- 类似地,V3+和Cr3+的CFSE分别为-4/5 ΔO和-6/5 ΔO。
对于Cr2+配合物,它有四个d电子,情况更复杂。现在我们可以得到高自旋构型(t2g)3(eg)1,或者低自旋构型(t2g)4(eg)0,其中两个电子配对。这两种状态的能量是多少?
- 高自旋:CFSE = (-3)(2/5)ΔO + (1)(3/5)ΔO = -3/5 ΔO
- 低自旋:CFSE = (-4)(2/5)ΔO + P = -8/5 ΔO + P,其中P是配对能
- 能量差 = -8/5 ΔO + P - (-3/5 ΔO) = -ΔO + P
配对能P是在同一轨道中放置两个电子的能量损失,这是由于电子之间的静电排斥引起的。对于3d元素,P的典型值为约15,000 cm-1。
这里的重要结果是,如果ΔO > P,则配合物将是低自旋的,如果ΔO < P,则配合物将是高自旋的。
由于ΔO取决于金属和配体,因此它决定了配合物的自旋态。

经验法则
- 3d配合物在与弱场配体结合时为高自旋,在与强场配体结合时为低自旋。
- 高价3d配合物(例如,Co3+配合物)倾向于低自旋(ΔO较大)
- 4d和5d配合物始终为低自旋(ΔO较大)
请注意,高自旋和低自旋状态仅发生在具有4到7个d电子的3d金属配合物中。具有1到3个d电子的配合物可以在t2g组的各个轨道中容纳所有电子。具有8、9或10个d电子的配合物将始终具有完全填充的t2g轨道和2-4个eg组中的电子。
高自旋和低自旋配合物的例子
- [Co(H2O)62+]包含一个d7金属离子,以及一个弱场配体。根据磁化率测量,已知该配合物为高自旋,每个分子具有三个未成对电子。其轨道占据情况为(t2g)5(eg)2。
- 我们可以计算CFSE为-(5)(2/5)ΔO + (2)(3/5)ΔO = -4/5 ΔO。
- [Co(CN)64-]也是一个八面体d7配合物,但它包含CN-,这是一种强场配体。其轨道占据情况为(t2g)6(eg)1,因此它有一个未成对电子。
- 在这种情况下,CFSE为-(6)(2/5)ΔO + (1)(3/5)ΔO + P = -9/5 ΔO + P。
过渡金属配合物的磁性
具有未成对电子的化合物具有固有的磁矩,该磁矩源于电子自旋。此类化合物与外加磁场发生强烈的相互作用。它们的磁化率提供了一种简单的方法来测量过渡金属配合物中未成对电子的数量。
如果过渡金属配合物没有未成对电子,则它是抗磁性的,并且会被弱排斥到不均匀磁场的高场区域。具有未成对电子的配合物通常是顺磁性的。顺磁体中的自旋在施加的磁场中独立排列,但在没有磁场的情况下不会自发排列。此类化合物会被磁铁吸引,即它们会被拉入不均匀磁场的高场区域。吸引力可以用古伊天平或超导量子干涉仪磁强计测量,它与配合物的磁化率(χ)成正比。
在没有自旋-轨道耦合的情况下,离子的有效磁矩(µeff)由其自旋和轨道矩之和给出
- µeff = µspin + µorbital = µs + µL
在八面体3d金属配合物中,轨道角动量在很大程度上被对称性“猝灭”,因此我们可以近似为
- µeff ≈ µs
我们可以使用以下公式根据未成对电子数(n)计算µs
这里µB是玻尔磁子(= eh/4πme)= 9.3 x 10-24 J/T。这个仅自旋公式对于第一排过渡金属配合物来说是一个很好的近似,尤其是高自旋配合物。下表比较了具有1-5个未成对电子的八面体配合物的µeff的计算值和实验测量值。
离子 未成对
电子
数目仅自旋
磁矩 /μB观察值
磁矩 /μBTi3+ 1 1.73 1.73 V4+ 1 1.68–1.78 Cu2+ 1 1.70–2.20 V3+ 2 2.83 2.75–2.85 Ni2+ 2 2.8–3.5 V2+ 3 3.87 3.80–3.90 Cr3+ 3 3.70–3.90 Co2+ 3 4.3–5.0 Mn4+ 3 3.80–4.0 Cr2+ 4 4.90 4.75–4.90 Fe2+ 4 5.1–5.7 Mn2+ 5 5.92 5.65–6.10 Fe3+ 5 5.7–6.0
这些八面体配合物与仅自旋公式存在的小偏差可能是由于忽略了轨道角动量或自旋-轨道耦合造成的。四面体d3、d4、d8和d9配合物往往比相同离子的八面体配合物表现出更大的偏离仅自旋公式的现象,因为在四面体情况下,轨道贡献的猝灭效果较差。
高自旋和低自旋配合物规则总结

- 3d配合物:可以是高自旋或低自旋,具体取决于配体(d4、d5、d6、d7)
- 4d和5d配合物:始终为低自旋,因为ΔO较大
- 最大CFSE出现在d3和d8情况下(例如,Cr3+、Ni2+),与弱场配体(H2O、O2-、F-等)结合,以及在d3-d6与强场配体结合时(Fe2+、Ru2+、Os2+、Co3+、Rh3+、Ir3+等)。
- Irving-Williams 级数。对于 M2+ 配合物,配合物的稳定性遵循以下顺序:Mg2+ < Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ > Zn2+。这种趋势表示随着离子变小(在元素周期表中从左到右),路易斯酸性增加,同时也反映了 CFSE 的趋势。气相 M2+ 离子的水合焓也反映了同样的趋势,如右侧图表所示。请注意,Ca2+、Mn2+ 和 Zn2+ 分别是 d0、d5(高自旋)和 d10 水合离子,它们都具有零 CFSE,并位于同一条线上。与该线偏差最大的离子,例如 Ni2+(八面体 d8),具有最高的 CFSE。

过渡金属配合物的颜色和光谱
过渡金属配合物通常具有美丽的颜色,因为如上所述,它们的 d-d跃迁能量可能位于光谱的可见光部分。对于八面体配合物,这些颜色较淡(跃迁较弱),因为它们违反了拉波特选择定则。根据该定则,在中心对称配合物中,g → g 和 u → u 跃迁是被禁止的。d 轨道具有 g( gerade )对称性,因此 d-d 跃迁是拉波特禁阻的。然而,当分子振动时,八面体配合物可以暂时偏离中心对称性而吸收光。自旋翻转也受到自旋选择定则的光学跃迁禁阻,因此激发态将始终与基态具有相同自旋多重度。
即使是最简单的过渡金属配合物的光谱也相当复杂,因为 d 电子填充 t2g 和 eg 轨道的多种可能方式。例如,如果我们考虑一个 d2 配合物,例如 V3+(aq),我们知道这两个电子可以位于五个 d 轨道中的任何一个,并且可以是自旋向上或自旋向下。对于 d2 配合物,实际上有 45 种这样的排列(称为微观态),它们不违反泡利不相容原理。通常我们只关心能量最低的六个,其中两个电子占据 t2g 集中各个轨道,并且它们的自旋全部向上或向下对齐。

当我们考虑 [Cr(NH3)6]3+ 离子的 d-d 跃迁时,我们可以看到这些微观态如何在电子光谱中发挥作用。该离子为 d3,因此三个 t2g 轨道中的每一个都包含一个未成对电子。我们预计当 t2g 轨道中的三个电子之一被激发到空的 eg 轨道时会发生跃迁。有趣的是,我们发现可见光区不仅有一个,而是两个跃迁。
我们看到两个跃迁的原因是电子可以来自 t2g 轨道中的任何一个,并最终进入 eg 轨道中的任何一个。为了论证起见,让我们假设电子最初位于 dxy 轨道中。它可以被激发到 dz2 或 dx2-y2 轨道
- dxy --> dz2 (较高能量)
- dxy --> dx2-y2 (较低能量)
第一个跃迁的能量较高(波长较短),因为在激发态时,构型为 (dyz1dxz1dz21)。所有三个激发态轨道都具有一定的 z 分量,因此 d 电子密度沿 z 轴“堆积”。因此,电子-电子排斥增加了该跃迁的能量。在第二种情况下,激发态构型为 (dyz1dxz1dx2-y21),并且 d 电子更对称地分布在金属周围。这种效应导致 d-d 带分裂约 8,000 cm-1。我们可以通过对称性证明所有其他可能的跃迁都等效于这两个跃迁之一,因此我们只看到 Cr3+ 配合物的两个可见吸收带。


过渡金属配合物最重要的非八面体几何形状是
- 4 配位:平面正方形和四面体
- 5 配位:四方锥和三角双锥


非八面体几何形状中 d 轨道的能量。左侧的图显示了当我们通过沿 z 轴拉长八面体配合物(四方畸变)、去除一个配体形成四方锥或去除沿 z 轴的两个配体形成平面正方形配合物时,d 轨道能级图会发生什么变化。在所有情况下,我们通过使 xy 平面中的键变短来保持总键级相同,因为 z 方向的键被拉伸和/或断裂。
偏离八面体对称性的畸变打破了 t2g 和 eg 轨道的简并性。具有 z 轴分量的 d 轨道(dxz、dyz、dz2)能量降低,而位于 xy 平面中的轨道(dxy、dx2-y2)能量升高。重心(加权平均轨道能量)保持不变。此外,需要注意的是,dxy 和 dx2-y2 轨道之间的分裂在 ΔO 上是恒定的,而不管畸变的性质如何。在平面正方形几何形状中,dxz、dyz、dz2、dxy 和 dx2-y2 轨道的能量分别为 -0.51、-0.40、+0.21 和 +1.21(以 ΔO 为单位)。
为什么“快乐”的八面体配合物会想要失去两个配体形成平面正方形配合物?这在 d8 和有时在 d9 配合物中经常发生,并且具有较大的 ΔO,即具有强场配体的 3d8 配合物以及具有任何配体的 4d8、5d8 配合物。这种 d8 配合物的例子包括 [Ni(CN)4]2-、抗癌药物顺铂(顺式-Pt(NH3)2Cl2)、[Pd(H2O)4]2+ 和 [AuCl4]-。在 d8 电子数下,最低四个轨道被填充,最高轨道(dx2-y2)为空,导致较大的 CFSE(2.4 ΔO,而八面体 d8 为 1.2 ΔO)。对于 4d8 和 5d8 配合物以及具有强场配体的 3d8 配合物,这 1.2 ΔO 的差异超过了配对能量。这些平面正方形配合物是反磁性的,并且往往非常稳定。对于弱场配体,3d8 配合物是八面体和顺磁性的(例如 [Ni(H2O)6]2+,其在 eg 轨道中具有两个未成对电子)。
催化中的平面正方形配合物

平面正方形 d8 配合物可以通过两个电子被氧化成八面体(低自旋)d6 配合物,后者也具有较大的 CFSE。由于失去两个电子伴随着获得两个配体,因此该过程称为氧化加成。相反的过程称为还原消除。这两个过程一起在催化循环中发挥作用,例如使用威尔金森催化剂进行烯烃的氢化。[10][11]左侧显示了催化循环。
催化剂在4配位的Rh(I) (4d8)和6配位的Rh(III) (4d6)之间循环。该络合物首先氧化加成H2,生成一个六配位络合物,其中氢的形式为H-。烯烃分子利用其π电子与金属配位,取代溶剂分子。该络合物通过将烯烃插入金属-氢键中进行重排,这一过程称为**迁移插入**。最后,该络合物通过消除氢化烯烃(还原消除)恢复到平面正方形几何构型。威尔金森催化剂活性很高,广泛用于均相氢化、硼氢化和氢硅烷化反应。[12][13]使用手性膦配体,该催化剂可以将前手性烯烃氢化得到对映体纯产物。[14]使用占据平面正方形络合物四个配位位点中的三个的五配位手性配体,可以生产非常高产率的对映体纯氢化产物。类似的手性Ir(I)络合物催化前手性酮的氢化生成手性伯醇,这是许多手性药物化合物生产中的重要步骤。[15]

线性ML2络合物。Cu(I)、Ag(I)和Au(I)离子与弱场和强场配体都形成线性ML2络合物。例如,在氰化物盐存在下,金或银金属发生空气氧化,形成[Ag(CN)2]-或[Au(CN)2]-,这种氧化还原反应被用于开采这些贵金属。不溶性的Ag(I)化合物,例如AgCl,可以在氨溶液中溶解形成可溶性线性络合物,例如[Ag(NH3)2]+。
线性配位几何结构源于s和d轨道的杂化。例如,在上图所示的[Au(CN)2]-离子中,5dz2和6s轨道的杂化体各含有一个电子,并沿z轴方向,类似于HC≡CH等分子中pz和s轨道杂化的方式。在这些线性络合物中,晶体场分裂成三个能级,其中填充的dxy和dx2-y2轨道能量最低,填充的dxz和dyz轨道能量居中,半填充的dz2轨道能量最高。dxz、dyz轨道与CN- π*轨道之间的反馈键也发生了,进一步稳定了络合物。[16][17]
5.7 Jahn-Teller效应
[edit | edit source]
Jahn–Teller效应,有时也称为Jahn–Teller畸变,描述了与某些电子构型相关的分子和离子的几何畸变。这种电子效应以赫尔曼·阿瑟·雅恩和爱德华·泰勒的名字命名,他们使用群论证明了轨道简并的分子不可能是稳定的。[18]Jahn–Teller定理本质上指出,任何具有空间简并电子基态的非线性分子都会发生几何畸变,从而消除这种简并性,因为畸变降低了分子的总能量。
我们可以在八面体金属络合物的背景下理解这种效应,方法是考虑eg轨道集中包含一个或三个电子的d电子构型。其中最常见的是高自旋d4(例如,CrF2)、低自旋d7(例如,NaNiO2)和d9(例如,Cu2+)。如果络合物可以发生畸变以破坏对称性,则一个(以前)简并的eg轨道能量将降低,另一个能量将升高。更多的电子将占据较低的轨道而不是较高的轨道,导致电子能量的整体降低。当t2轨道部分填充时,四面体络合物中也会发生类似的畸变。这种降低电子能量的几何畸变被称为电子驱动的。类似的电子驱动的畸变发生在一维链状化合物中,在那里它们被称为Peierls畸变,以及二维键合薄片中,在那里它们被称为电荷密度波。


Jahn–Teller效应最常出现在八面体络合物中,尤其是六配位铜(II)络合物。[19]该离子的d9电子构型在两个简并的eg轨道中产生了三个电子,导致双重简并的电子基态。这种络合物沿分子四重轴之一(始终标记为z轴)发生畸变,这会消除轨道和电子简并性并降低总能量。畸变通常采用沿z轴延长与配体键合的方式,但偶尔也表现为这些键的缩短(Jahn–Teller定理并没有预测畸变的方向,只预测了不稳定几何构型的存在)。当发生这种伸长时,其作用是降低路易斯碱性配体上的电子对与任何具有z分量的轨道中的电子之间的静电排斥,从而降低络合物的能量。如果未畸变的络合物预计具有反演中心,则在畸变后将保持该中心。
在八面体络合物中,当奇数个电子占据eg轨道时,Jahn–Teller效应最为明显。这种情况出现在具有d9、低自旋d7或高自旋d4构型的络合物中,所有这些络合物都具有双重简并的基态。在这些化合物中,参与简并的eg轨道直接指向配体,因此畸变会导致较大的能量稳定。严格来说,当由于t2g轨道中的电子而导致简并时,也会发生这种效应(即诸如d1或d2之类的构型,它们都是三重简并的)。然而,在这种情况下,这种效应不太明显,因为在使配体远离t2g轨道的过程中,排斥的降低要小得多,而t2g轨道并没有直接指向配体(见下表)。四面体络合物(例如锰酸盐([MnO4]2-,d1)也是如此:畸变非常细微,因为当配体没有直接指向轨道时,获得的稳定性较小。
八面体配位的预期效应在下表中给出。
| d电子数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 高/低自旋 | 高自旋 | 低自旋 | 高自旋 | 低自旋 | 高自旋 | 低自旋 | 高自旋 | 低自旋 | ||||||
| J-T效应强度 | 弱 | 弱 | 强 | 弱 | 弱 | 弱 | 弱 | 强 | 强 | |||||
弱:弱Jahn–Teller效应(t2g轨道不均匀占据)
强:预期强Jahn–Teller效应(eg轨道不均匀占据)
空白:预期无Jahn–Teller效应。
Jahn–Teller效应在某些化合物的紫外-可见吸收光谱中表现出来,在那里它通常会导致谱带分裂。它在许多铜(II)络合物的结构中很容易显现。[20]可以从低温电子自旋共振光谱的精细结构获得有关此类络合物各向异性和配体结合性质的更多详细信息。
5.8 四面体络合物
[edit | edit source]四面体络合物由后过渡金属离子(Co2+、Cu2+、Zn2+、Cd2+)和一些早期过渡金属(Ti4+、Mn2+)形成,尤其是在配体较大的情况下。在这些情况下,小的金属离子不容易容纳大于4的配位数。四面体离子和小分子的例子有[CoCl4]2-、[MnCl4]2-和TiX4(X = 卤素)。在一些氧阴离子中也观察到四面体配位,例如[FeO4]4-,它作为离散阴离子存在于盐Na4FeO4和Sr2FeO4中,以及在中性氧化物RuO4和OsO4中。金属羰基络合物Ni(CO)4和Co(CO)4]-也是四面体。


可以通过连接四面体的顶点形成一个立方体来理解四面体晶体场中d轨道的分裂,如左侧的图片所示。四面体M-L键位于立方体的体对角线上。dz2和dx2-y2轨道指向笛卡尔坐标轴,即指向立方体的面,并且与配体孤对电子的接触最少。因此,这两个轨道形成一个低能量的双重简并e组。dxy、dyz和dxz轨道指向立方体的边缘,并形成一个三重简并t2组。虽然t2轨道与配体轨道的重叠比e组多,但与八面体络合物的eg轨道相比,它们仍然是弱相互作用的。
所得晶体场能级图如图右侧所示。分裂能Δt大约是使用相同配体形成的八面体络合物分裂能的4/9。对于3d元素,Δt因此相对于配对能很小,并且它们的四面体络合物总是高自旋。请注意,我们已经删除了“g”下标,因为四面体没有对称中心。
四面体配合物通常具有鲜艳的颜色,因为它们缺乏对称中心,而对称中心会禁止 d-d*跃迁。由于低能级跃迁是允许的,因此这些配合物通常在可见光范围内吸收,并且消光系数比相应的八面体配合物高 1-2 个数量级。在干燥剂中可以看到这种效应的一个例子,干燥剂包含无色无水硫酸钙(石膏)颗粒,这些颗粒可以吸收气体中的水分。干燥剂中的指示剂染料是氯化钴(II),湿润时为浅粉色(八面体),干燥时为深蓝色(四面体)。可逆水合反应为
晶体场稳定化能 (CFSE) 是过渡金属配合物稳定性的一个重要因素。具有高 CFSE 的配合物倾向于热力学稳定(即,它们具有较高的 Ka 值,Ka 是金属-配体缔合的平衡常数),并且也动力学惰性。它们在动力学上是惰性的,因为配体取代需要它们在过渡态中解离(失去一个配体),缔合(获得一个配体)或交换(同时获得和失去配体)。如果 CFSE 很大,即使配体交换反应的产物也是稳定的配合物,这些配位几何的扭曲也会导致较大的活化能。因此,Pt4+、Ir3+(均为低自旋 5d6)和 Pt2+(平面正方形 5d8)的配合物具有非常缓慢的配体交换速率。
还有其他两个重要因素有助于配合物的稳定性
- 金属和配体的硬软相互作用(与配合物形成的能量有关)
- 螯合效应,它是配合物稳定性的熵贡献者。
硬软相互作用
硬酸通常是小尺寸、高电荷密度、弱极化性阳离子,例如 H+、Li+、Na+、Be2+、Mg2+、Al3+、Ti4+ 和 Cr6+。电正性金属处于高氧化态通常是硬酸。这些元素主要存在于氧化物矿物中,因为 O2- 是硬碱。
一些硬碱包括 H2O、OH-、O2-、F-、NO3-、Cl- 和 NH3。
硬酸-碱相互作用主要是静电的。硬酸与硬碱的配合物由于 CFSE 的静电成分而稳定。
软酸是大尺寸、可极化、电负性金属离子处于低氧化态,例如 Ni0、Hg2+、Cd2+、Cu+、Ag+ 和 Au+。
软碱是阴离子/中性碱,例如 H-、C2H4、CO、PR3、R2S 和 CN-)。软酸通常以硫化物或砷化物矿物形式存在于自然界中。
软酸和软碱之间的键合主要是共价的。例如,金属羰基通过零价或低价金属与中性 CO 之间的共价相互作用结合形成 Ni(CO)4、Fe(CO)5、Co(CO)4-、Mn2(CO)10、W(CO)6 及相关化合物。
硬硬和软软相互作用的偏好(“相似相吸”)在卤化铜的性质中得到了很好的说明
- CuF CuI
- 不稳定 稳定
- CuF2 CuI2
- 稳定 不稳定
CuF 和 CuI2 化合物从未被分离出来,并且在热力学上不稳定,会发生歧化反应
- 2 CuF(s) → Cu(s) + CuF2(s)
- 2 CuI2(s) → 2 CuI(s) + I2(s)
我们将在第 9 章中进一步了解这些化合物的能量学定量。

含有两个以上金属离子结合位点的配体称为螯合配体(源于希腊语 χηλή,chēlē,意为“爪”)。顾名思义,螯合配体对金属离子的亲和力高于仅具有一个结合基团(称为单齿 =“单齿”)的配体。
考虑水溶液中的两个络合平衡,一方面是钴(II)离子 Co2+(aq) 与乙二胺 (en),另一方面是氨 NH3。
- [Co(H2O)6]2+ + 6 NH3 ⇌ [Co(NH3)6]2+ + 6 H2O (1)
- [Co(H2O)6]2+ + 3 en ⇌ [Co(en)3]2+ + 6 H2O (2)
在电子方面,氨和 en 配体非常相似,因为两者都通过 N 结合,并且它们的氮原子的路易斯碱强度相似。这意味着两个反应的 ΔH° 必须非常相似,因为在每种情况下都会形成六个 Co-N 键。然而,有趣的是,我们观察到第二个反应的平衡常数比第一个反应大 100,000 倍。
这两个反应之间的主要区别在于,第二个反应涉及更少粒子的“缩合”来形成配合物。这意味着这两个反应的熵变是不同的。第一个反应的 ΔS° 值接近于零,因为方程两侧的分子数相同。第二个反应的 ΔS° 为正,因为四个分子聚合在一起,但产生了七个分子。它们之间的差异 (ΔΔS°) 约为 +100 J/mol-K。我们可以使用以下公式将其转换为平衡常数的比率
- Kf(en)/Kf(NH3) = e-ΔΔG°/RT ≈ e+ΔΔS°/R ≈ e12 ≈ 105


底线是螯合效应是熵驱动的。由此可见,配体包含的结合基团越多,ΔS° 越正,配合物形成的 Kf 就越高。在这方面,六齿配体乙二胺四乙酸 (EDTA) 是形成八面体配合物的最佳配体,因为它具有六个结合基团。在所有四个 COOH 基团都去质子的碱性溶液中,EDTA4- 配体的螯合效应大约为 1015。这意味着,对于给定的金属离子,Kf 对于 EDTA4- 比在相同浓度下相关单齿配体的 Kf 大 1015 倍。EDTA4-牢固地结合元素周期表中几乎所有 2+、3+ 或 4+ 离子,并且是分析应用和分离的非常有用的配体。
大环效应遵循与螯合效应相同的原理,但该效应因配体的环状构象而进一步增强。大环配体不仅是多齿的,而且由于它们以共价方式限制在其环状形式,因此它们允许更少的构象自由度。据说配体“预组织”用于结合,并且围绕金属离子包裹几乎没有熵损失。例如,血红素 b 是一种四齿环状配体,它强烈络合过渡金属离子,包括(在生物系统中)Fe+2。
下面显示了一些其他常见的螯合和环状配体


乙酰丙酮 (acac-,右) 是一种阴离子双齿配体,通过两个氧原子与金属离子配位。acac- 是硬碱,因此它更喜欢硬酸阳离子。对于二价金属离子,acac- 形成中性挥发性配合物,例如 Cu(acac)2 和 Mo(acac)2,这些配合物可用于金属薄膜的化学气相沉积 (CVD)。
2,2'-联吡啶和相关的双齿配体,如 1,10-菲咯啉(下方,左中)与 Ru2+ 等金属形成螺旋桨状配合物。[Ru(bpy)3]2+ 配合物(下方左)具有光致发光性,也可以发生光氧化还原反应,使其成为光催化和人工光合作用的有趣化合物。[Ru(bpy)3]2+ 等金属多吡啶配合物的螺旋桨形状巧合地与 DNA 主沟的大小和螺旋性相匹配。这导致了对沿着 DNA 骨架进行电子转移反应的一些有趣的研究,这些反应由金属配合物的光激发引发。
冠醚,如 18-冠-6(下方,右中),是环状硬碱,可以络合碱金属阳离子。根据环中环氧乙烷单元的数量,冠醚可以选择性地结合 Li+、Na+ 或 K+。
- 冠醚的螯合性质与天然抗生素缬氨霉素(右下图)类似,后者可以选择性地将K+离子跨过细菌细胞膜运输,通过耗散其膜电位杀死细菌。与冠醚一样,缬氨霉素也是一种环状硬碱。
过渡金属配合物可以交换一个配体以换取另一个配体,这些反应在其合成、立体化学和催化化学中都很重要。化学反应的机理与其反应动力学密切相关。与有机化学一样,过渡金属反应的机理通常是从实验中推断出来的,这些实验检查了进入和离开配体对反应速率的浓度依赖性、中间体的检测以及反应物和产物的立体化学。
热力学与动力学。当我们考虑过渡金属配合物的反应时,务必记住其热力学和动力学之间的区别。例如,形成平面四方形四氰合镍酸盐配合物
- Ni2+(aq) + 4 CN-(aq) ⇌ [Ni(CN)4]2- (aq) Keq ≈ 1030 M-4
从热力学上讲,[Ni(CN)4]2-非常稳定,这意味着上述平衡非常偏向于右侧。然而,从动力学上讲,该配合物是不稳定的,这意味着它可以快速交换其配体。例如,13C标记的CN-离子与结合的CN-配体之间的交换发生在数十毫秒的时间尺度上
- [Ni(CN)4]2- (aq) + *CN-(aq) ⇌ [Ni(CN)3(*CN)]2- + CN-(aq) kexchange ≈ 102 M-1s-1
相反,化合物可以是热力学不稳定但动力学惰性的,这意味着它需要相对较长的时间才能发生反应。例如,[Co(NH3)6]3+离子在酸性条件下不稳定,但它与浓盐酸的水解反应在大约一周内才能在室温下完成

- [Co(NH3)6]3+(aq) + 6 H3O+(aq) ⇌ [Co(H2O)6]3+(aq) + 6 NH4+(aq) Keq ≈ 1030
亨利·陶伯通过简单的试管实验研究了配体交换反应的机理,将过渡金属配合物分类为不稳定的,如果其反应半衰期为一分钟或更短,则为惰性的,如果它们需要更长的时间才能反应。配体取代速率的动态范围非常大,至少跨越了15个数量级。在大多数实验室实验的时间尺度上,陶伯对不稳定性的定义对于将反应分类为具有低活化能和高活化能的反应是有用的。正如我们将看到的,晶体场稳定化能 (CFSE)在决定活化能以及配体取代速率方面起着关键作用。
晶体场稳定化能和配体交换速率。让我们考虑一个非常常见且简单的配体交换反应,即在八面体[M(H2O)6]n+配合物中用另一个水分子取代一个水分子。由于产物(除了标记外)与反应物相同,因此我们知道此反应的ΔG° = 0且Keq = 1。通过使用同位素标记的水(通常含有17O或18O)可以通过核磁共振监测反应的进程

关于这个(否则很无聊的)反应最引人注目的事情是不同金属离子和氧化态的速率常数的巨大差异——大约14个数量级
| Mn+ | log k (sec-1) |
|---|---|
| Cr3+ | |
| V2+ | |
| Cr2+ | |
| Cu2+ |

虽然起初似乎很奇怪,同一个离子在两种不同的氧化态(Cr3+与Cr2+)下分别是不稳定的或不稳定的,但我们可以通过绘制配合物的d轨道分裂图来开始解释这种差异。我们发现,具有高CFSE(Cr3+,V2+)的八面体配合物倾向于惰性。相反,在高能eg轨道上具有电子的离子(Cr2+,Cu2+)倾向于不稳定。在Cr3+和V2+的情况下,使配合物偏离八面体对称性(例如,形成5或7配位中间体)的能量损失特别高。对于Cr2+和Cu2+,配体取代的活化能较低,它们已经在反键eg轨道上具有电子。
根据我们为计算过渡金属配合物的CFSE制定的规则,我们现在可以预测配体取代速率的趋势
- 具有d3和d6(低自旋)构型的八面体配合物,例如Cr3+(d3)、Co3+(d6)、Rh3+(d6)、Ru2+(d6)和Os2+(d6)由于其高CFSE而倾向于取代惰性。
- 平面正方形d8配合物,尤其是4d和5d系列中的配合物,也取代惰性。例如,Pd2+、Pt2+和Au3+的配合物。
- 中间情况是Fe3+、V3+、V2+、Ni2+和主族离子(Be2+、Al3+)的配合物,它们是硬路易斯酸。这些配合物形成强的金属-氧键,并且水交换速率在101-106 s-1范围内。
- CFSE为零的离子在纳秒的时间尺度上交换水分子(k ≈ 108-109 s-1)。这些包括具有d0、d5(高自旋)和d10电子数的离子,包括碱金属(Li+、Na+、K+、Rb+、Cs+)和碱土金属(Mg2+、Ca2+、Sr2+、Ba2+)阳离子、Zn2+、Cd2+、Hg2+和Mn2+。在这些情况下,CFSE为零,并且破坏八面体对称性的能量成本相对较低。
- 对于p区元素,较大的离子交换速度更快(例如,Ba2+ > Ca2+和Ga3+ > Al3+),因为路易斯酸强度随着离子尺寸的增加而降低。
- Cu2+离子(d9)作为Jahn-Teller离子,已经偏离了八面体对称性,因此非常不稳定,以大约108 s-1的速率交换水配体。
配体取代机理。对于经历配体取代的MLn配合物,基本上有三种不同的反应机理
- 在解离机理中,MLn配合物首先失去一个配体形成MLn-1中间体,然后进入的配体Y与MLn-1片段反应
- L(n-1)M-L* ⇌ L(n-1)M- + L* ⇌ L(n-1)M-Y
下图说明了八面体ML6配合物的配体取代。本例中的中间态涉及三角双锥ML5片段以及游离的L和Y配体。

如果速率决定步骤是L从配合物中解离,则Y的浓度不影响反应速率,导致一级速率定律
在八面体配合物的情况下,此反应将是一级ML6和零级Y,但前提是最高能量过渡态是ML5中间体形成之前的过渡态。如果两个过渡态的能量接近(如右侧动画所示),则速率定律变得更加复杂。在这种情况下,我们可以通过假设MLn中间体的稳态浓度较低来简化问题。得到的速率定律为
当 k2[Y] >> k-1[L] 时,该反应简化为更简单的二级反应速率方程。由于过渡态的形成涉及配体的解离,因此在解离机理中,活化熵总是正的。
- 在缔合机理中,进入的配体 Y 进攻 MLn 配合物,瞬时形成 MLnY 中间体,然后中间体失去一个配体 L,形成 MLn-1Y 产物。
经历缔合取代的配合物通常要么是配位不饱和的,要么包含一个可以改变其与金属键合方式的配体,例如,硝酰配体 (NO) 的配位数或弯曲的变化。在均相催化中,缔合途径是理想的,因为结合事件,以及因此反应的选择性,不仅取决于金属催化剂的性质,还取决于参与催化循环的分子。

缔合机理的例子通常存在于 d8 平方平面金属配合物的化学中,例如 Vaska 配合物 (IrCl(CO)[P(C6H5)3]2) 和四氯铂酸盐(II)。这些化合物 (ML4) 与进入的 (取代的) 配体 Y 结合形成五配位中间体 ML4Y,然后在后续步骤中解离其一个配体。虽然进入的配体最初结合在赤道位置,但Berry 拟旋转 为所有配体提供了在赤道和轴向位置之间进行采样的低能途径。根据微观可逆原理,配体的解离必须发生在赤道位置。Y 的解离不会导致反应,但 L 的解离会导致净取代,生成 d8 配合物 ML3Y。第一步通常是速率决定步骤。因此,活化熵为负,这表明过渡态的秩序增加。缔合反应遵循二级动力学:产物出现速率取决于 ML4 和 Y 的浓度。

反式效应与缔合机理有关,它控制着某些配体取代反应的立体化学。
反式效应是指使反式于某些其他配体的配体(后者被称为反式导向配体)更容易发生反应。反式配体的活化归因于电子效应,在平面正方形配合物中最为显著,但也可在八面体配合物中观察到。[21]顺式效应 最常在八面体配合物中观察到。
除了动力学反式效应外,反式配体也会影响分子的基态,其中最显著的是键长和稳定性。一些作者更倾向于使用反式影响一词来区分它与动力学效应,[22]而另一些作者则使用更具体的术语,如结构反式效应或热力学反式效应。[21]
反式效应的发现归功于Ilya Ilich Chernyaev,[23]他在 1926 年认识到它并为其命名。[24]
反式效应的强度(以反式配体取代速率的增加来衡量)遵循以下顺序
- F−,H2O,OH− < NH3 < py < Cl− < Br− < I−,SCN−,NO2−,SC(NH2)2,Ph− < SO32− < PR3,AsR3,SR2,CH3− < H−,NO,CO,CN−,C2H4
请注意,弱场配体往往是较差的反式导向配体,而强场配体则是强反式导向配体。
反式效应的经典例子是顺铂及其反式异构体的合成。[25]从 PtCl42− 开始,第一个 NH3 配体随机添加到四个等效位置中的任何一个。然而,由于 Cl− 的反式效应大于 NH3,因此第二个 NH3 添加到 Cl− 的反式位置,因此与第一个 NH3 为顺式。
另一方面,如果从 Pt(NH3)42+ 开始,则获得反式产物。
平方配合物中的反式效应可以用上面描述的缔合机理来解释,该机理通过三棱柱形中间体进行。具有高动力学反式效应的配体通常是那些具有高 π 酸性(如膦的情况)或低配体孤对电子-dπ 排斥(如氢化物的情况)的配体,它们更倾向于中间体中更具 π 碱性的赤道位置。第二个赤道位置被进入的配体占据。第三个也是最后一个赤道位置被离开的反式配体占据,因此净结果是动力学上有利的产物是反式于具有最大反式效应的配体的配体被消除的产物。[22]
- 交换机理类似于缔合和解离途径,只是没有形成明显的 MLnY 或 MLn-1 中间体。这种协同机理可以认为类似于有机化学中四面体碳原子上的 SN2 途径的亲核取代。交换机理进一步分类为缔合 (Ia) 或解离 (Id),具体取决于过渡态中 M-Y 和 M-L 键合的相对重要性。如果过渡态的特征是形成强的 M-Y 键,则机理为Ia。相反,如果 M-L 键的削弱在达到过渡态中更为重要,则机理为Id。
Ia 机理的一个例子是 [V(H2O)6]2+ 中本体水和配位水的交换。相反,稍紧凑的离子 [Ni(H2O)6]2+ 离子通过Id 机理交换水。[26]
离子对的影响。带高电荷的阳离子配合物倾向于与阴离子配体形成离子对,而这些离子对通常通过Ia途径发生反应。静电结合的亲核进入配体可以与第一配位层中的配体交换位置,从而导致净取代。一个说明性的过程是铬(III) 六水配合物的“加阴离子”(与阴离子反应)
- [Cr(H2O)6]3+ + SCN− ⇌ {[Cr(H2O)6], NCS}2+
- {[Cr(H2O)6], NCS}2+ ⇌ [Cr(H2O)5NCS]2+ + H2O
- 讨论螯合配体及其作用,并举一些新的例子。
- 解释(并举一些新的例子)我们如何知道金属离子的八面体配合物是高自旋还是低自旋,以及我们可以进行哪些测量来确认它。
1. 预测下列配合物的分子几何形状,并确定每个配合物是抗磁性还是顺磁性。
(a) [Fe(CN)6]3-
(b) [Ru(ox)3]4- (ox = 草酸根,C2O4)
(c) [Ag(CN)2]-
(d) [W(CO)6]
(e) [Ir(NH3)4]+
2. 对于下列每个过渡金属配合物,给出 (i) d 电子数,(ii) 配合物的近似分子几何形状,以及 (iii) 显示 d 轨道的分裂和填充的能级图。
(a)[Os(CN)6]3-
(b)顺式-PtCl2(NH3)2
(c) [Cu(NH3)4]+
3. 八面体过渡金属配合物可以是高自旋或低自旋。四面体和平面正方形配合物是否也如此?解释原因。
4. 对于下表中的每个过渡金属配合物,给出与观察到的磁矩一致的电子构型(在 t2g 和 eg 组的 3d 轨道内)。
| 化合物 | µ (BM) |
|---|---|
| [Fe(CN)6]3- | 1.8 |
| [Fe(NH3)5(H2O)]3+ | 6.1 |
| [Fe(NCS)6]4- | 5.0 |
| [Cr(acac)3] | 3.9 |
5. 对于以下每对配合物,确定晶体场稳定化能较高的配合物(并展示你的计算过程)。
(a) [Mn(CN)6]3- 与 [Mn(CN)6]4-
(b) [Ni(en)2]2+ 与 [Cd(en)2]2+,其中 en = H2NCH2CH2NH2
(c) [Cr(H2O)6]3+ 与 [Mn(H2O)6]2+
6. 在用 FeCl3 与过量的乙二胺四乙酸 (EDTA) 在中性 pH 条件下混合制成的溶液中,Fe3+(aq) 离子的浓度约为 10-17 M。然而,在乙二胺和乙酸浓度相当的溶液中,Fe3+(aq) 浓度约为 10-7,即高出 1010 倍。解释原因。
7. 配合物 [VO(H2O)5]2+ 为蓝色,而与另一种单齿中性配体 L 相似的配合物 [VO(L)5]2+ 为黄色。以下哪些陈述是正确的?简要解释。
(a) L 比 H2O 是更强的场配体。
(b) [VO(L)5]2+ 是高自旋配合物。
(c) [VO(L)5]2+ 吸收黄光。
(d) 这两个配合物都含有一个与金属相关的 3d 电子。
8. OH- 和 NH3 都是布朗斯台德碱,并且都可以与金属离子形成配合物。解释为什么 OH- 可以比 NH3 成为更强的布朗斯台德碱,同时在光谱化学序列中却处于更低的位置。
9. [Ni(H2O)6]2+ 溶液呈浅绿色且顺磁性 (µ = 2.90 BM),而 [Ni(CN)4]2- 溶液呈黄色且反磁性。
(a) 绘制每个配合物的分子几何形状和 d 轨道能级图,并显示 d 轨道的电子占据情况。
(b) 解释磁性和颜色的差异。
10. W. Deng 和 K. W. Hipps (J. Phys. Chem. B 2003, 107, 10736-10740) 报道了对 Ni(II) 四苯基卟啉 (NiTPP) 电子性质的 STM 研究,NiTPP 是一种红紫色、中性的反磁性配合物,通过使 Ni(II) 高氯酸盐与四苯基卟啉反应制得。当 NiTPP 与硫氰酸钠反应时,会形成另一种顺磁性配合物。绘制 NiTPP 和产物配合物的结构,以及解释每种结构的晶体场能级图。你预计顺磁性配合物的磁矩值(以 μB 为单位)是多少?

11. 过渡金属配合物可以发生配体交换反应,其中游离配体或溶剂分子取代了其中一个结合的配体。由于反应物和产物配合物通常具有不同的颜色,因此可以在“试管”反应中轻松测量配体交换速率。化学上相同的配体(例如,结合的水分子与游离的水分子)的交换也可以通过核磁共振波谱和其他方法测量。有趣的是,对于不同的金属离子和氧化态,水的交换速率变化范围达 14 个数量级。在某些情况下,一个水分子需要几周才能与另一个水分子交换。而在其他情况下,交换的时间尺度为纳秒。
(a) 存在一个总趋势(见右侧图),即金属氧化态越高,交换速率越慢。解释这种趋势。晶体场稳定化能与反应动力学有什么关系?
(b) 除了你的 (a) 中的答案外,解释你观察到的二价金属离子水交换速率的任何趋势。
(c) Cu2+ 具有特别快的的水交换速率。为什么?
(d) 图中交换速率最慢的二价、三价和四价金属离子的水合配合物的几何形状和 d 电子数是多少?它们具有特别高或低的 CFSE 吗?解释。
12. 主族离子的配体交换速率沿族向下增加,例如 Al3+ < Ga3+ < In3+。对于过渡金属离子,我们观察到相反的趋势,例如 Fe2+ > Ru2+ > Os2+。解释为什么这些趋势不同。
13. Seppelt 及其同事在盐 [AuXe4]2+ (Sb2F11-)2 中报道了非常不寻常的离子 [AuXe4]2+(Science 2000, 290, 117-118)。这是首次报道含有金属与稀有气体原子之间键合的化合物。绘制该离子的 d 轨道能级图,并预测它应该是反磁性还是顺磁性。你预计是否能够使用 Cu 代替 Au 或 Kr 代替 Xe 来形成类似的配合物?为什么或为什么不?
14. 对于反应 顺式-Mo(CO)4L2 + CO → Mo(CO)5L + L,发现反应速率对于两种不同的配体 L 变化了 500 倍,但对 CO 气体的压力相对不敏感。(a) 这种反应有什么类型的机理?(b) 活化体积和活化熵的符号是什么?
15. 在 Rosenberg 最初发现顺式-Pt(NH3)2Cl2 的生物效应时,该化合物是由于 Pt 阳极在含有葡萄糖和氯化镁的电解质溶液中部分溶解而意外产生的。[27] 电解反应还产生少量铵离子。解释从机理上讲为什么在这种条件下选择性地形成顺式异构体。
- ↑ Rosi, Nathaniel L.; Eckert, Juergen; Eddaoudi, Mohamed; Vodak, David T.; Kim, Jaheon; O'Keefe, Michael; Yaghi, Omar M. (2003). "微孔金属有机框架中的储氢". 科学. 300 (5622): 1127–1129. Bibcode:2003Sci...300.1127R. doi:10.1126/science.1083440. PMID 12750515.
- ↑ Green, M.L.H. (1995). "元素共价化合物的新分类方法". 有机金属化学杂志. 500: 127–148. doi:10.1016/0022-328X(95)00508-N.
- ↑ CBC 方法,Parkin 研究组,哥伦比亚大学。
- ↑ Crabtree, Robert. 过渡金属有机化学:第 4 版。Wiley-Interscience,2005
- ↑ "金属-配体多重键:含氧代、氮化物、亚氨基、亚烷基或烷基炔配体的过渡金属配合物的化学" W. A. Nugent 和 J. M. Mayer;Wiley-Interscience,纽约,1988。
- ↑ McConville, David H.; Wolf, Jennifer R.; Schrock, Richard R. (1993). "手性钼 ROMP 引发剂和全顺式高度立体规整聚(2,3-(R)2降冰片烯) (R = CF3 或 CO2Me) 的合成". 美国化学会志. 115 (10): 4413–4414. doi:10.1021/ja00063a090.
- ↑ Nguyen, Sonbinh T.; Johnson, Lynda K.; Grubbs, Robert H.; Ziller, Joseph W. (1992). "降冰片烯在质子介质中通过 VIII 族卡宾配合物进行开环复分解聚合 (ROMP)". 美国化学会志. 114 (10): 3974–3975. doi:10.1021/ja00036a053.
- ↑ Rosenberg B,Vancamp L,Trosco JE,Mansour VH(1969)。“铂化合物——一类新型有效的抗肿瘤药物”。自然。222(5191):385-386。doi:10.1038/222385a0。
{{cite journal}}:CS1 维护:使用了作者参数(链接) - ↑ G. Wilkinson,M. Rosenblum,M. C. Whiting,R. B. Woodward(1952)。“二茂铁的结构”。美国化学学会杂志。74(8):2125-2126。doi:10.1021/ja01128a527。
{{cite journal}}:CS1 维护:作者列表有多个名称(链接) - ↑ Osborn,J. A.;Jardine,F. H.;Young,J. F.;Wilkinson,G.(1966)。“三(三苯基膦)卤代铑(I)的制备和性质及其一些反应,包括烯烃和炔烃及其衍生物的催化均相氢化”。化学学会杂志A:1711-1732。doi:10.1039/J19660001711。
{{cite journal}}:CS1 维护:作者列表有多个名称(链接) - ↑ “三(三苯基膦)卤代铑(I)” J. A. Osborn,G. Wilkinson,《无机合成》,1967年,第10卷,第67页。DOI 10.1002/9780470132418.ch12
- ↑ D. A. Evans,G. C. Fu和A. H. Hoveyda(1988)。“铑(I)催化的烯烃硼氢化。环状和非环状体系中区域和立体化学控制的文献记录”。J. Am. Chem. Soc。110(20):6917-6918。doi:10.1021/ja00228a068。
- ↑ I. Ojima,T. Kogure(1972)。“使用硅烷-铑(I)配合物组合选择性还原α,β-不饱和萜类羰基化合物”。四面体Lett。13(49):5035-5038。doi:10.1016/S0040-4039(01)85162-5。
- ↑ W. S. Knowles(2003)。“不对称氢化(2001年诺贝尔演讲)”。高级合成与催化。345(12):3-13。doi:10.1002/adsc.200390028。
- ↑ J. Yu,J. Long,W. Wu.,P. Xue和X. Zhang(2017)。“铱催化的酮不对称氢化,使用易得且模块化的二茂铁基氨基膦酸(f-Ampha)配体”。有机快报。19(3):690-693。doi:10.1021/acs.orglett.6b03862。
{{cite journal}}:CS1 维护:作者列表有多个名称(链接) - ↑ M. De Santis 等人,造币金属(I)氰化物中的化学键和s-d杂化,Inorg. Chem. 2019, 58, 11716-11729。https://pubs.acs.org/doi/full/10.1021/acs.inorgchem.9b01694
- ↑ N. Zhang,J. Kou和C. Sun,金浸出配合物中金-配体相互作用的研究:DFT研究,Molecules 2023, 28, 1508。https://doi.org/10.3390/molecules28031508
- ↑ H. Jahn和E. Teller(1937)。“简并电子态下多原子分子的稳定性。I. 轨道简并”。皇家学会会刊A。161(905):220-235。Bibcode:1937RSPSA.161..220J。doi:10.1098/rspa.1937.0142。
- ↑ Rob Janes和Elaine A. Moore(2004)。金属-配体键合。英国皇家化学学会。ISBN 0-85404-979-7。
- ↑ Patrick Frank,Maurizio Benfatto,Robert K. Szilagyi,Paola D'Angelo,Stefano Della Longa和Keith O. Hodgson“ [Cu(aq)]2+的溶液结构及其对蓝色铜蛋白活性位点中架桥诱导键合的影响”无机化学2005,第44卷,第1922-1933页。DOI 10.1021/ic0400639
- ↑ a b Coe,B. J.;Glenwright,S. J. 八面体过渡金属配合物中的反式效应。配位化学评论2000,203,5-80。
- ↑ a b Robert H. Crabtree(2005)。过渡金属有机化学(第4版)。新泽西州:Wiley-Interscience。ISBN 0-471-66256-9。
- ↑ Kauffmann,G. B. 伊利亚·伊里奇·切尔尼亚耶夫(1893-1966)和反式效应。J. Chem. Educ.1977,54,86-89。
- ↑ Chernyaev,I. I. 二价铂的单亚硝酸盐。I. Ann. inst. platine(苏联)1926,4,243-275。
- ↑ George B. Kauffman,Dwaine O. Cowan(1963)。“顺式和反式-二氯二氨合铂(II)”。《无机合成》(Inorg. Synth)。7:239–245。doi:10.1002/9780470132388.ch63。
{{cite journal}}:CS1 维护:使用了作者参数(链接) - ↑ Helm,Lothar;Merbach,André E.(2005)。“无机和生物无机溶剂交换机制”。《化学评论》(Chem. Rev)。105(6):1923–1959。doi:10.1021/cr030726o。PMID 15941206。
- ↑ Rosenberg,B.;Van Camp,L.;Krigas,T.(1965)。“铂电极电解产物对大肠杆菌细胞分裂的抑制”。《自然》(Nature)。205(4972):698–9。doi:10.1038/205698a0。PMID 14287410。












![{\displaystyle {\ce {Rate={{\mathit {k}}_{1}[ML_{\mathit {n}}]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f19546a5039b36de5f4c4fd594797bc0df9b999)
![{\displaystyle {\ce {Rate}}={\frac {k_{1}k_{2}[{\ce {Y}}][{\ce {ML_{\mathit {n}}}}]}{{k_{-1}[{\ce {L}}]}+k_{2}[{\ce {Y}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccc9e0dfadba0e61ce35c386afdc89e901198c08)

