无机化学导论/材料的电子性质：超导体和半导体

  第 10 章：材料的电子性质：超导体和半导体

现代集成电路包含数十亿个纳米级晶体管和二极管，这些器件对逻辑和存储功能至关重要。这两种器件都依赖于含几百万分之一硼或磷杂质的结晶硅区域之间的结。

在第 6 章中，我们从原子轨道出发，构建了固体金属晶体的分子轨道，为金属发展了一个能带图。这种处理方法使我们对电子在金属中的行为有了有用的认识，即电子以非常快的速度在散射事件之间移动，并在电场中以缓慢的漂移速度迁移。它还告诉我们，金属是一种具有部分填充能带的物质，这意味着费米能级穿过其一个轨道能带。绝缘体或半导体具有类似的能带图，只是能带要么完全填充，要么完全空缺。在这种情况下，费米能级位于完全占据能带和空缺能带之间的带隙中。本章我们将看到，半导体的性质（以及它们有用的电子应用）取决于少量杂质（“掺杂剂”）的添加，这些杂质会改变费米能级的位置，从而导致电子或“空穴”的导电。

虽然能带图适用于大多数晶体材料，但它并没有告诉我们固体导电的全部故事。这是因为能带模型（就像 MO 理论一样）基于单电子模型。这是我们在讨论 MO 理论之初做出的一个近似值：我们使用氢类（单电子）薛定谔方程解来给出 s、p、d 和 f 原子轨道的形状。在单电子原子中，这些轨道在一个给定的壳层内是简并的，例如 2s 和 2p 轨道之间的能级差只有在我们考虑一个电子在原子中其他电子的场中的能量时才会出现。从原子到分子，我们进行线性组合生成单电子分子轨道（以及在固体中的单电子能带）。但与多电子原子一样，对于包含许多电子的真实分子和固体，情况并非如此简单。电子相互排斥，因此它们在分子和固体中的运动是相关的。虽然这种效应在像钠这样的“良好”金属中很弱 - 其中波函数高度离域 - 但它在其他材料中（如过渡金属氧化物）可能非常重要。相关的电子效应导致由温度、压力或成分的微小变化驱动的金属-绝缘体转变，以及超导性 - 在低温下电流以零电阻通过。在本章中，我们将开发一些简单的模型来理解这些有趣且重要的固体电子性质。

第 10 章的学习目标

• 解释哈伯德模型和莫特模型对金属-绝缘体转变的物理基础。
• 理解为什么良好的超导体来自不良的金属。
• 了解半导体的结构和能带隙及颜色在周期表中的趋势。
• 从本征半导体的电导率随温度变化的关系获得能带隙。
• 预测杂质或缺陷引入半导体时产生的掺杂类型。
• 将能带图和费米能级与 n 型或 p 型掺杂相关联。
• 了解二极管、LED、太阳能电池和 FET 工作原理的物理基础。
• 解释晶体半导体和非晶半导体的结构和电子性质的差异。

  10.1 金属-绝缘体转变

被“锡疫”破坏的管风琴管

在第 6 章中，我们了解到金属和绝缘体不仅具有不同的电学性质，而且还具有非常不同的晶体结构。金属倾向于具有高配位数（通常为 8 或 12），而绝缘体具有低配位数，可以合理化为“八隅体”键合排列。例如，在结晶 Si 或 Ge（金刚石结构）中，每个原子都有四个最近的邻居。每条键有两个电子，因此每个原子在其价层中有八个电子。Sn，位于 Ge 之下的元素，存在两种不同的形式，一种（灰锡）具有金刚石结构，是一种脆性窄带隙半导体，另一种（白锡）具有体心四方结构，是一种延展性金属。这两种形式的能量非常接近，事实上，金属白锡在低温下转变为脆性半导体灰锡形式。18 世纪欧洲的极寒天气导致许多锡管风琴管断裂，最终变成粉末。这种转变被称为锡疫、锡病、锡虫或锡麻风病。粉末实际上是灰锡，它不像其金属表亲白锡那样具有延展性。

在实验可及的温度和压力下，Si 和 Ge 始终是半导体（即绝缘体），而 Pb 始终是金属。为什么 Sn 不同？原因在于轨道重叠。理论告诉我们，事实上，任何（和所有）绝缘体在足够高的压力下，或者更确切地说，在足够高的密度下，应该变成金属。然而，对于大多数绝缘体来说，所需的压力远远超过我们在实验室中所能达到的压力。

我们如何才能合理化绝缘体向金属状态的转变？事实上，我们如何才能理解绝缘体本身的存在？

电子在原子的一维链中跳跃。

随着原子链的密度和原子之间轨道重叠程度的增加，能量与 DOS 的关系。增加的重叠将中性原子和阴离子-阳离子态扩展为能带，每个能带都具有带宽 Δ。当 Δ 超过哈伯德间隙 U 时，会突然发生向金属态的转变。

哈伯德模型。让我们考虑一个像我们在第 6 章中所做的那样，由大量 (N) 原子组成的链。为了方便起见，我们可以说这些原子是像 H、Na 或 Cs 这样的原子，它们只有一个价电子。我们之前发展的简单能带模型表明该链应该是金属的，因为N 个原子结合形成N 个轨道，而N 个价电子只填充了轨道能带的一半。但这一结论不依赖于密度，这造成了一个悖论。如果链中的原子相距很远，我们怀疑电子应该局域在原子中。

J. Hubbard 在 1963 年提出了这个问题的解决方案。 Hubbard 考虑了将电子从一个原子转移到其最近邻居所需的能量，如右侧图片所示。由于每个原子已经有一个电子（自旋随机），将电子移到另一个原子需要克服电子-电子排斥的能量，从而形成一个阳离子-阴离子对。对于相距较远的原子，这种能量 (U) 由下式给出

U = IP - EA - e²/4πε₀d

其中 IP 和 EA 分别是电离能和电子亲和能，ε₀ 是自由空间的介电常数，方程中的最后一项表示阳离子和阴离子之间的库仑吸引力。对于像碱金属这样的原子，U 在 3-5 eV 的数量级上，这远大于热能 kT。因此，我们预计在室温下几乎没有阴离子-阳离子对，并且原子链应该是绝缘体。

当我们将原子挤在一起时会发生什么？在哈伯德模型中，随着原子之间距离的减小，中性原子态和阴离子-阳离子态的能量都会扩展成能带，每个能带都有带宽 Δ。较低的能带可以容纳恰好N 个电子（而不是我们之前在 MO 图像中开发的2N），因为每个轨道只能容纳一个电子而不会发生自旋配对。因此，对于较小的 Δ，较低的能带是满的，而较高的能带是空的。然而，当我们继续压缩该链时，轨道重叠变得非常强，以至于 Δ ≈ U。此时，能带重叠，一些电子填充阴离子-阳离子态。然后该链变得导电，材料变成金属。

二氧化钒具有金红石结构，在未扭曲状态下呈金属态，每个 V 原子有一个价电子。晶格扭曲会导致 V 原子成对，从而形成电子绝缘态。金属-绝缘体转变可以通过改变温度、压力或轨道占有率来可逆地驱动。VO₂ 中这种转变的电切换正在被研究用于高性能薄膜晶体管中的应用。^[2]

一些材料，例如 Sn 和 VO₂，恰好具有合适的轨道重叠程度，使得通过改变温度或压力可以发生哈伯德转变。此类材料对电切换非常有用，如右侧金红石结构 VO₂ 所示。大多数材料远离转变，处于金属态或绝缘态。过渡金属单氧化物 MO（M = Ti、V、Cr、Mn、Fe、Co、Ni）中可以看到一个有趣的周期性趋势，说明了这一概念，它们都具有 NaCl 结构。TiO 和 VO 呈金属态，因为 3d 轨道在结构中具有显著的重叠。然而，CrO、MnO、FeO、CoO 和 NiO 都是绝缘体，因为 3d 轨道收缩（因此 Δ < U）跨过过渡金属系列。相反，类似的硫化物（TiS、VS，……NiS）都是金属态。硫化物具有 NiAs 结构，其中所有金属原子沿着堆叠轴（六方 c 轴）重叠。沿着该轴的短金属-金属距离导致强轨道重叠，使得 Δ > U。

莫特模型。 1949 年，Neville Mott 提出了一个更简单、更少原子模型的金属-绝缘体转变模型。^[3] 莫特模型考虑了材料中电子作为所有其他价电子密度的函数的行为。我们知道对于一个电子氢样原子（H、Na、Cs 等），薛定谔方程包含一个势能项

V(r) = -(e²/4πε₀r)

这个势能函数产生了氢原子中熟悉的允许能级梯度。然而，在金属中，必须修改这个库仑势，以包括固体中其他电子对核电荷的屏蔽。在这种情况下，存在一个屏蔽库仑势

V(r) = -(e²/4πε₀r)exp(-qr)

其中 q 是屏蔽长度的倒数，由下式给出

q² = 4m_e²(3n/π)^1/3(2π/h)

低浓度（顶部，离子导体）和较高浓度（底部，金属）下液氨中锂金属的溶液。来自 Joshua Judkins 的视频

这里 n 是原子（或价电子）密度，m_e 是电子质量，h 是普朗克常数。在远大于屏蔽长度 q^-1 的距离处，电子不再“感受到”原子核上的电荷。莫特表明，存在一个临界电子密度 n_c，在此密度之上，价电子不再受单个原子核的束缚，可以自由地在晶体中游动。这个临界密度标志着向金属态的转变，由莫特准则给出

n_c^1/3a_H ≈ 0.26

在这个方程中，a_H 是低密度极限下价电子的有效玻尔半径，例如计算 Cs 金属的值时，Cs 原子 6s 壳层中电子的平均轨道半径。

莫特模型中的重要概念是，金属-绝缘体转变与价电子密度密切相关。这与哈伯德的轨道重叠模型一致，但更一般，因为它不依赖于原子的周期性结构。因此，莫特模型适用于诸如溶解在液氨中的金属原子、困在冷冻气体基质中的金属原子以及半导体中的掺杂剂等多种系统。^[4] 在某些系统中，可以用相当惊人的结果连续调整价电子密度。例如，将碱金属（Li、Na，……）溶解在液氨（沸点 -33 ^oC）中会产生蓝色的液体。溶剂化的碱金属阳离子和带负电的电子赋予蓝色液氨溶液离子电导率（如盐溶液），但没有电子电导率。但是，随着电子浓度的增加，会形成反射性的青铜色液体相，浮在蓝色相之上。这种青铜色相是金属态的，具有很高的电导率。最终，加入足够的碱金属，整个液体将转化为电子导电的青铜色相。

VO₂ 之间绝缘相和金属相的电切换（见上文）也可以用莫特转变来解释。增加电子密度（通过化学或电场掺杂）会增加价电子的浓度，从而推动相变为金属态。

热力学和相变。 热力学上，金属-绝缘体转变是一级相变。在这种转变中，结构和性质会突然发生变化（想想麦当劳的早餐到午餐的转变——在 10:30 AM 之前，没有办法在午饭后吃煎饼，或在午餐前吃汉堡！^[5]）。因此，在 Sn 金属的情况下，结构变化（从四配位到八配位）和电子电导率变化（从绝缘体到金属）同时发生。与冰到水到蒸汽等其他一级相变一样，转变过程中存在一个潜热，并且导数性质（如热容）存在不连续性。

右侧显示了 V₂O₃ 的典型金属-绝缘体转变相图。八面体配位的 V³⁺ 离子具有 d² 电子数，因此每个原子有两个未配对自旋，在低温下，晶格中的自旋反铁磁有序。正如我们在第 8 章中学到的那样，在奈尔温度以上，反铁磁体变成顺磁体，这也是莫特绝缘体。增加压力，或用电子掺杂（例如，用一些 d³ Cr³⁺ 替代 V³⁺）会将电子密度推过莫特转变，自旋配对，固体变成金属态。

  10.2 超导体

磁铁悬浮在用液氮冷却的高温超导体之上。持续电流在超导体表面流动，排斥磁铁的磁场。这种电流有效地形成一个排斥磁铁的电磁铁。

超导性是指材料中电流以零电阻流动。此类材料对于电磁铁的应用非常重要，例如在磁共振成像 (MRI) 和核磁共振 (NMR) 机器中，因为一旦电流开始在这些磁铁线圈中流动，它就不会停止。利用超导体进行磁悬浮——在临界场强以下，超导体是完美的抗磁体，不会被磁通线穿透——也可能与未来技术相关，例如磁悬浮列车。

超导现象，1911 年由昂内斯在 Hg 金属中首次发现，至今仍只是部分了解。它对于物理学家来说是一个宏观量子现象，对于试图制造更好的超导体（尤其是那些在更高温度下超导的超导体）以及由此衍生出来的器件（例如超导量子干涉器件 (SQUIDs)，它们是极其灵敏的磁强计）的化学家和材料科学家来说，是一个令人非常感兴趣的现象。

自旋配对和零电阻。 从金属态到超导态的转变与玻色-爱因斯坦凝聚和超流性的量子现象有关。单个电子自旋 = 1/2，因此是费米子（具有半整数自旋的粒子）。由于泡利不相容原理，不超过两个费米子可以占据相同的量子态（例如分子或固体中的轨道）。这个规则的常见结果是自旋配对电子的每个能级上的轨道填充。相反，具有整数自旋的粒子——称为玻色子——没有这种限制，任何数量的玻色子都可以占据相同的量子化能级。

当电子自旋配对成所谓的库珀对时，就会发生超导性，它们可以一起穿过晶格。库珀对中的电子，尽管是自旋配对的，但它们之间有着长距离的关系：库珀对在铜氧化物超导体中的空间范围为几个纳米，而在铝等低 T_c 超导体中，空间范围可以达到一个微米。由于其总自旋角动量为零，库珀对是玻色子。当温度足够低时，库珀对“凝聚”到最低能级。第二个最低能级——通常比基态高几 meV——只要能隙大于热能 kT，它们就无法进入。然后，电子被晶格散射变得不可能，因为散射会耗散能量，库珀对不能改变其能量状态。因此，电阻（如我们在第 6 章中学到的那样，电阻源于散射）在 T_c 以下突然下降到零。然而，当库珀对快速移动时，它们会被分解，因此超导体在超过某个临界电流密度 j_c 时（即使在 T_c 以下）也会变回普通金属。这种现象也与使超导性消失的临界磁场 H_c 相关。

电子弹簧床。是什么导致电子由于其负电荷而相互排斥，但在超导体中配对并一起移动？这种机制——必须涉及电子之间某种吸引作用——对于具有相对较低转变温度的“传统”超导体来说是众所周知的，但对于高温氧化物超导体来说，目前尚不清楚。在传统或BCS 超导体中，自旋配对是由晶格介导的，如左侧图所示。强烈的电子-晶格相互作用会导致电子穿过晶格时产生晶格畸变。这种弹性形变会被反方向移动的第二个电子感受到，并表现为一种吸引力。这可以被认为类似于两个人在蹦床上跳跃的相互作用。第一个人在蹦床上产生的重量会产生一个“井”，吸引第二个，因此他们倾向于一起移动（即使他们不喜欢对方）。这种相互作用看起来很奇怪，但它得到了实验的支持，例如 T_c 的同位素效应，以及对传统超导体中 T_c 值的定量预测。

超导材料的时间轴，显示 T_c 与发现年份的关系。

不良金属制成良好的超导体。所有超导体在其临界转变温度 T_c 以上都是“正常”金属——具有有限的电阻。如果你问在元素周期表中的哪个位置可以找到超导体，答案会让人惊讶。最具导电性的金属（Ag、Au、Cu、Cs 等）是最差的超导体，即它们具有最低的超导转变温度，在许多情况下低于 0.01 K。相反，“不良”金属，如铌合金、某些氧化铜、K_xBa_1-xBiO₃、MgB₂、FeSe 和 C₆₀^n- 阴离子的碱金属盐，可以具有相对较高的转变温度。

我们观察到，大多数良好的超导体在组成空间中非常接近金属-绝缘体转变。根据我们的微观图像，超导体中的轨道重叠很差，仅足以使其在 T_c 以上表现为金属（Δ ≈ U）。在正常状态下，具有高 T_c 的超导体——最高可达 150 K——通常是“不良”金属。这种金属的一个重要特征是电子的平均自由程（在正常状态下，高于 T_c）约等于晶格间距，即仅几个 Å。相比之下，我们在第 6 章中了解到，像 Au、Ag 和 Cu 这样的良好金属的电子平均自由程要长两个数量级（约 40 nm）。在不良金属中，电子“强烈”地感受到晶格，而在良好金属中，电子对金属原子间距离的微小变化不敏感。

不良金属的通用 E 与 DOS 图。

不良金属的能带图像是什么样的？关键在于，由于轨道重叠很差，金属在费米能级处具有高态密度。这是高温超导体的一种普遍特性，为寻找新型和改进的超导材料提供线索。回想一下，3d 系列中间的过渡元素（Cr、Fe、Co、Ni）由于轨道重叠差和弱的 d-d 键合而具有磁性。这些元素下面的元素——尤其是 Nb、Ta 和 W——只有足够的 d-d 轨道重叠，才能处于金属-绝缘体转变的金属侧，成为“不良”金属。这些元素的碳化物和氮化物通常是超导体，其中碳和氮原子用于调节价电子密度，如以下表格所示。

YBa₂Cu₃O_7-δ（YBCO）的晶体结构，这是第一个 T_c 超过液氮沸点的超导体。

化合物	NbC	Mo2N	TaC	VN	NbN	TaN	Nb3Ge
Tc (K)	11.1	5.0	9.7	7.5	15.2	17.8	22.3

铜酸盐超导体 La_2-xSr_xCuO₄ 的晶体结构和相图。（LSCO）

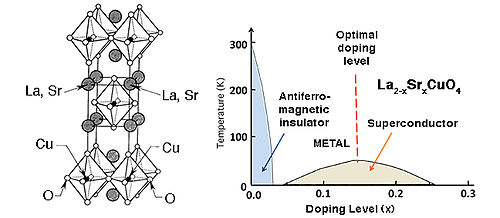
高温超导体。除了在金属态下具有弱的轨道重叠——这会导致 E_F 处的高 DOS 外，高温超导体通常还包含处于混合氧化态（例如 Cu^2+/3+ 或 Bi^3+/5+）的元素，这些元素在能量上接近晶格中的 O^2-/O^- 对。在环境压力下，铜酸盐超导体具有已知的最高 T_c 值，范围约为 35 到 150 K。这些材料的晶体结构几乎都是钙钛矿晶格的变体，如右侧所示的 1-2-3 超导体 YBa₂Cu₃O_7-δ。理想的钙钛矿晶格的化学式为 ABO₃ = A₃B₃O₉。在 YBa₂Cu₃O_7-δ 中，Y 和 Ba 占据 A 阳离子位置，Cu 占据 B 位置，并且九个 O 原子中的两个缺失。

YBa₂Cu₃O_7-δ 晶格由混合价态的铜（II/III）氧化物片组成，这些片由氧原子覆盖，形成 CuO₅ 平方锥体。这些片包围着 Y³⁺ 阳离子。共享平方锥体顶端氧原子的铜（II）氧化物带沿着结构中的一个方向延伸。在 YBa₂Cu₃O_7-δ 和相关材料中，结构的一个组成部分（此处为 Cu-O 带）充当电荷储层，以控制平面 CuO₂ 片的掺杂，这些片是承载超电流的结构元素。包含 Bi、Tl 或 Hg 的电荷储层层和单元晶胞中多个重叠的 CuO₂ 片的铜酸盐超导体倾向于具有最高的 T_c 值。

金属-绝缘体转变与超导性之间的联系在 La_2-xSr_xCuO₄ 的相图中得到了很好的说明，La_2-xSr_xCuO₄ 是第一个铜酸盐超导体，于 1986 年由 Georg Bednorz 和 K. Alex Müller 发现。这种化合物具有相当简单的结构，其中岩盐 La(Sr)O 层与钙钛矿 La(Sr)CuO₃ 层交织在一起。未掺杂的 La₂CuO₄ 仅包含 Cu²⁺ 离子，是一种反铁磁绝缘体。当少量 Sr²⁺ 取代 La³⁺ 时，一些 Cu²⁺ 被氧化为 Cu³⁺，并且晶格被空穴掺杂。随着掺杂水平的增加，反铁磁相经历一级相变到“不良”金属，并且在略高的掺杂密度下，超导相出现。超导相与金属-绝缘体转变的接近性是铜酸盐超导体的标志。在 x = 0.15 时观察到 35K 的最大 T_c。更高水平的掺杂使费米能级超出了 Cu 的 d 带中最高 DOS 的点，然后超导相逐渐消失。有趣的是，将此相图与 V₂O₃ 的相图进行比较（上面），V₂O₃ 在掺杂时也会经历反铁磁绝缘体到“不良”金属的转变。

  10.3 元素周期律：金属、半导体和绝缘体

当我们考虑材料电子性质的元素周期律时，重要的是回顾我们在前面章节中学习的一些关键键合趋势。

• 在元素周期表中向下移动，固体中的原子倾向于采用具有更高配位数的结构。
• 元素周期表的第二行很特殊，具有强烈的 s-p 杂化和原子之间的 π 键合。
• 较高量子壳中的电子结合得较弱，因此对于较重的原子，键合和反键合轨道之间的能级差变小。

我们还知道，元素周期表中的大多数元素都是金属，但右上角的元素在普通条件下（1 个大气压）是绝缘体，并且倾向于在它们的化合物中遵循八隅律。

在元素周期表中金属和非金属之间的过渡处，我们遇到了电子性质的交叉，以及其他性质的交叉，例如氧化物的酸性（见第 3 章）。位于边界的一组元素松散地称为类金属。这些元素中的几种（例如 C、Sn 和 As）可以以不同的同素异形体存在，这些同素异形体可以是金属、绝缘体或介于两者之间。

通过考虑这些元素（以及许多化合物）的能带结构和电子电导率的温度依赖性，可以更严格地描述它们的电子性质。正如我们之前讨论的那样，金属具有部分填充的能带，这意味着费米能级与部分填充的能带相交。随着温度的升高，金属的导电性变差，因为晶格振动（在物理学文献中称为声子）散射了移动的价电子。相反，具有填充和空带的半导体和绝缘体在较高温度下导电性更好，因为一些电子被热激发到最低的空带。绝缘体和半导体之间的区别是任意的，从金属-绝缘体转变的角度来看，所有半导体都是绝缘体。如果材料的带隙 (E_gap) 小于约 3 eV，我们通常称绝缘体为半导体。半金属是一种带隙接近零的材料，例如单层 sp² 键合碳（石墨烯）和元素 Bi。与窄带隙半导体一样，半金属在较高温度下具有更高的电导率。

  10.4 半导体：带隙、颜色、电导率和掺杂

从 GaAs 单晶切出的 2 英寸晶圆。GaAs 与许多 p 区半导体一样，具有闪锌矿结构。

如上所述，半导体的定义多少有些任意性，指的是带隙能<3.0 eV（约 290 kJ/mol）的绝缘体。之所以选择这个临界值，是因为我们会看到，未掺杂半导体的电导率随带隙能呈指数下降，而在 3.0 eV 时，电导率非常低。此外，带隙更宽的材料（例如 SrTiO₃，E_gap = 3.2 eV）不会吸收可见光谱范围内的光。

在元素周期表中，我们可以找到一些半导体。

• 早期过渡金属氧化物和氮化物，特别是那些具有 d⁰ 电子数的氧化物，如 TiO₂、TaON 和 WO₃。
• 后期 3d 元素的氧化物，如 Fe₂O₃、NiO 和 Cu₂O。
• 具有 d⁰、d² 和 d⁶ 电子数的层状过渡金属硫属化物，包括 TiS₂、ZrS₂、MoS₂、WSe₂ 和 PtS₂。
• d¹⁰ 铜和银卤化物，例如 CuI、AgBr 和 AgI。
• p 区元素的闪锌矿和纤锌矿结构化合物，尤其是那些与 Si 或 Ge 等电子化合物，例如 GaAs 和 CdTe。虽然这些是最常见的，但也存在其他非等电子且具有不同结构的 p 区半导体，包括 GaS、PbS 和 Se。

p 区八电子半导体是迄今为止研究最多、在技术应用中最重要的半导体，也是我们将详细讨论的半导体。

黄铜矿结构被 ABX₂ 八电子半导体（如 Cu^IIn^IIISe₂ 和 Cd^IISn^IVP₂）采用。由于阳离子的有序排列，晶胞相对于母体闪锌矿结构加倍。每个阴离子（黄色）与两种类型的阳离子（蓝色和红色）配位。

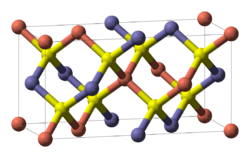
闪锌矿和纤锌矿结构半导体每 2 个原子有 8 个价电子。这些组合包括 4-4（Si、Ge、SiC 等）、3-5（GaAs、AlSb、InP 等）、2-6（CdSe、HgTe、ZnO 等）和 1-7（AgCl、CuBr 等）半导体。其他加起来为八电子配置的变化也是可能的，例如 Cu^IIn^IIISe₂，它具有黄铜矿结构，如右图所示。

带隙能如何随成分变化？有两个重要的趋势。

(1) 在元素周期表中向下移动一个族，带隙减小。

C（金刚石） >    Si   >     Ge   >    α-Sn

E_gap (eV):       5.4               1.1          0.7          0.0

可以通过回忆 E_gap 与成键和反键轨道之间的能量分裂有关来理解这种趋势。随着主量子数的增加，这种差异减小（键变得更弱）。

(2) 对于等电子化合物，离子性增加会导致更大的带隙。

Ge     <     GaAs     <    ZnSe

0.7             1.4              2.8 eV

Sn     <     InSb     <     CdTe     <     AgI

0.0             0.2              1.6              2.8 eV

这种趋势也可以从简单的 MO 图中理解，正如我们在第 2 章中讨论的那样。随着电负性差 Δχ 的增加，成键和反键轨道之间的能量差也随之增加。

色轮显示发射光的颜色和波长。

Fe₂O₃ 粉末因其 2.2 eV 带隙而呈现橙红色。

带隙是半导体的非常重要的性质，因为它决定了它的颜色和电导率。半导体的许多应用都与带隙有关。

• 窄带隙材料（Hg_xCd_1-xTe、VO₂、InSb、Bi₂Te₃）用作红外探测器和热电材料（将热能转换为电能）。
• 宽带隙材料（Si、GaAs、GaP、GaN、CdTe、CuIn_xGa_1-xSe₂）用于电子产品、发光二极管和太阳能电池。

半导体固溶体，如 GaAs_1-xP_x，具有介于端元化合物（在本例中为 GaAs 和 GaP，均为闪锌矿结构）之间的带隙。通常，成分和带隙之间存在线性关系，称为维加德定律。这条“定律”在实际材料中经常被违反，但仍然为设计具有特定带隙的材料提供了有用的指导。例如，红色和橙色发光二极管 (LED) 由具有 GaP_0.40As_0.60 和 GaP_0.65As_0.35 分别组成的固溶体制成。增加较轻元素 (P) 的摩尔分数会导致更大的带隙，从而导致发射光子的能量更高。

半导体的颜色。吸收和发射光的颜色都取决于半导体的带隙。可见光覆盖大约 390-700 nm 范围，或 1.8-3.1 eV。发射光的颜色从 LED 或半导体激光器对应于带隙能量，并且可以从右侧所示的色轮中读出。

吸收光的颜色包括带隙能量，但也包括所有更高能量（更短波长）的颜色，因为电子可以从价带激发到导带的一系列能量。因此，带隙位于红外区域的半导体（例如 Si，1.1 eV 和 GaAs，1.4 eV）看起来是黑色的，因为它们吸收所有可见光。宽带隙半导体（如 TiO₂，3.0 eV）是白色的，因为它们只吸收紫外线。Fe₂O₃ 的带隙为 2.2 eV，因此吸收 λ < 560 nm 的光。因此，它呈现橙红色（从 Fe₂O₃ 反射的光的颜色），因为它吸收绿光、蓝光和紫光。类似地，CdS (E_gap = 2.6 eV) 是黄色的，因为它吸收蓝光和紫光。

通过向半导体添加热量或光能 E > E_gap，会产生电子-空穴对（蓝色箭头）。电子-空穴对复合释放等于 E_gap 的能量（红色箭头）。

半导体中的电子和空穴。纯（未掺杂）半导体当电子被热量或光从价带激发到导带时，可以导电。电子 (e^-) 的激发会在价带中留下一个空穴 (h⁺)。空穴是键合轨道中没有电子的地方，也是一种可移动的电荷载流子，但带正电荷。空穴在晶格中的运动可以被视为类似于拥挤剧院中空座位的移动。如果每个人都向前移动一个座位，中间排的一个空座位可以移动到排尾（以容纳一位迟到看电影的人）。由于空穴的运动方向与电子运动方向相反，因此它在电场中充当正电荷载流子。

与产生电子-空穴对相反的过程是它们的复合。当导带电子下降到与价带空穴复合时，两者都会湮灭并释放能量。这种能量释放是 LED 发光的原因。

在平衡状态下，电子-空穴对的产生和湮灭以相同的速度进行。这种动态平衡类似于水中 H⁺ 和 OH^- 离子的解离-缔合平衡。我们可以写出质量作用表达式

n×p = K_eq = n_i²

其中 n 和 p 分别表示电子和空穴的数密度，单位为 cm^-3。本征载流子浓度 n_i 等于未掺杂半导体中电子或空穴的数密度，其中 n = p = n_i。

请注意，它与水的自电离方程式类似

[H⁺][OH^-] = K_w

通过类比，我们会看到，当我们增加 n（例如，通过掺杂）时，p 会减少，反之亦然，但它们的乘积在给定温度下将保持不变。

载流子浓度的温度依赖性。使用方程式 K_eq = exp(-ΔG^o/RT) 和 ΔG^o = ΔH^o – TΔS^o，我们可以写出

n×p = n_i² = exp(ΔS^o/R)exp(-ΔH^o/RT)

产生电子空穴对的熵变由下式给出

ΔS^o = R ln(N_C) + R ln(N_V) = R ln(N_CN_V)

其中 N_V 和 N_C 分别是价带和导带中的有效态密度。

因此，我们得到

n_i² = N_CN_V exp(-ΔH^o/RT)

由于体积变化可以忽略不计，所以 ΔH^o ≈ ΔE^o，因此 ΔH^o/R ≈ E_gap/k，由此我们得到

n_i² = N_CN_V exp(-E_gap/kT)

最后

n = p = n_i = (N_CN_V)^1/2 exp(-E_gap/2kT)

对于纯 Si (E_gap = 1.1 eV)，N ≈ 10²²/cm³，我们可以从该方程计算出在 300 K 时载流子密度 n_i 约为 10¹⁰/cm³。这比元素周期表中 Si 左侧的元素 Al 的价电子密度低大约 12 个数量级。因此，我们预计纯半导体的电导率比金属的电导率低很多个数量级。

本征半导体 Ge (E_gap = 0.7 eV)、Si (1.1 eV) 和 GaAs (1.4 eV) 的 ln(σ) 对 1/T 图。直线的斜率为 -E_gap/2k。

本征半导体的电导率。电导率 (σ) 是载流子数密度 (n 或 p)、电荷 (e) 和迁移率 (µ) 的乘积。回顾第 6 章，µ 是载流子漂移速度与电场之比，单位为 cm²/伏特-秒。通常，电子和空穴的迁移率略有不同（分别为 µ_e 和 µ_h），因此电导率由下式给出

σ = neµ_e + peµ_h

对于任何一种电荷载流子，我们从第 6 章回忆起迁移率 μ 由下式给出

μ = v_drift/E = eτ/m,

其中 e 是电荷的基本单位，τ 是散射时间，m 是电荷载流子的有效质量。

取电子和空穴迁移率的平均值，并使用 n = p，我们得到

σ = σ_o exp(-E_gap/2kT)，其中 σ_o = 2(N_CN_V)^1/2eµ。

通过测量电导率随温度的变化，可以得到传导的活化能，即 E_gap/2。这种图类似于阿伦尼乌斯图，如右图所示，对应于三种不同的未掺杂半导体。每种情况下直线的斜率为 -E_gap/2k。

半导体的 n 型和 p 型掺杂涉及将电子施主原子（浅橙色）或受主原子（蓝色）取代到晶格中。这些取代分别引入额外的电子或空穴，这些电子或空穴很容易被热能电离，成为自由载流子。掺杂半导体的费米能级比导带低几十毫伏（n 型）或比价带高几十毫伏（p 型）。

半导体的掺杂。半导体的几乎所有应用都涉及受控的掺杂，即在晶格中用杂质原子进行取代。微量的掺杂剂（百万分之几的范围）会显著影响半导体的电导率。因此，需要非常纯净的半导体材料，这些材料经过精心掺杂 - 既要考虑杂质原子的浓度，也要考虑其空间分布。

n型和p型掺杂。在晶体硅中，每个原子都有四个价电子，并与其相邻原子形成四个键。这恰好是完全填满半导体价带的电子数。将磷原子引入晶格（图中右边的带正电的原子）会增加一个额外的电子，因为磷有五个价电子，而它只需要四个电子来与其相邻原子形成键。在低温下，额外的电子与磷原子结合在一起，形成一个类似氢原子的分子轨道，由于半导体的介电常数很高，该轨道比孤立的磷原子中的3s轨道大得多。在硅中，这个“扩展的”玻尔半径约为42 Å，即比氢原子大80倍。电离这个电子（使它能够在晶格中自由移动）所需的能量只有大约40-50 meV，这比室温下的热能（26 meV）大不了多少。因此，费米能级正好位于导带边缘下方，并且在室温下，这些额外电子中很大一部分被提升到导带，在磷原子位点留下固定的正电荷。晶体是n型掺杂，这意味着多数载流子（电子）带负电荷。

或者，可以用硼代替晶格中的硅，从而实现p型掺杂，其中多数载流子（空穴）带正电荷。硼只有三个价电子，并从硅晶格“借”一个电子，形成一个带正电荷的空穴，该空穴存在于硼原子周围的大的类似氢原子的轨道中。通过将电子从价带提升到填充局部空穴状态，可以使该空穴离域。同样，这个过程只需要40-50 meV，因此在室温下，硼掺杂引入的空穴中很大一部分存在于离域的价带状态中。费米能级（在零温度下有50%的占据概率的电子能级）在p型半导体中正好位于价带边缘之上。

如上所述，半导体的掺杂会极大地改变它们的电导率。例如，硅在300 K时的本征载流子浓度约为10¹⁰ cm^-3。电子和空穴的质量作用平衡也适用于掺杂半导体，因此我们可以写成

n×p = n_i² = 10²⁰ cm^-6 at 300K

如果我们将磷以百万分之一的比例代替硅，则电子的浓度约为10¹⁶ cm^-3，因为晶体中大约有10²² 个硅原子/cm³。根据质量作用方程，如果n = 10¹⁶，则p = 10⁴ cm^-3。这个计算结果有三个后果

• 掺杂半导体中的载流子密度（10¹⁶ cm^-3）远高于未掺杂材料（~10¹⁰ cm^-3），因此电导率也高出几个数量级。
• 传导的激活能只有40-50 meV，因此电导率不会随温度发生很大变化（与本征半导体不同）。
• 少数载流子（在本例中为空穴）不参与导电，因为它们的浓度远低于多数载流子（电子）。

类似地，对于p型材料，电导率主要由空穴决定，也远高于本征半导体的电导率。

半导体掺杂的化学。有时，掺杂（n型或p型）是什么类型并不马上明了，这是因为半导体晶格被“破坏”了。除了在正常晶格位点上取代杂质原子（上面给出的硅的例子）之外，也可以用空位（缺少的原子）和间隙原子（位于通常不占据的位点的额外原子）来掺杂。一些简单的规则如下

• 对于取代，在元素周期表中添加右侧的原子会导致n型掺杂，而添加左侧的原子会导致p型掺杂。

例如，当TiO₂被Nb在一些Ti位点上掺杂，或被F在O位点上掺杂时，结果是n型掺杂。在这两种情况下，杂质原子都比被其取代的原子多一个价电子。类似地，在GaAs中用少量Zn取代Ga，或在NiO中用少量Li取代Ni，会导致p型掺杂。

• 阴离子空位会导致n型掺杂，而阳离子空位会导致p型掺杂。

例如，CdS_1-x和WO_3-x中的阴离子空位，两者都产生n型半导体，以及Cu_1-xO中的铜空位，产生p型半导体。

• 间隙阳离子（例如Li）向晶格提供电子，导致n型掺杂。间隙阴离子非常罕见，但会导致p型掺杂。

有时，在同一个晶体中可能同时存在p型和n型掺杂剂，例如硅晶格中的B和P杂质，或金属氧化物晶格中的阳离子和阴离子空位。在这种情况下，两种类型的掺杂会相互补偿，掺杂类型由浓度较高的掺杂剂决定。掺杂剂也可以存在于多个位点上。例如，Si可以在GaAs中同时占据Ga位点和As位点，并且两种取代相互补偿。然而，Si略微偏向Ga位点，导致n型掺杂。

  10.5 半导体p-n结

当p型和n型半导体连接在一起时，电子和空穴在界面处湮灭，留下一个耗尽区，该区域分别包含带正电和带负电的施主和受主原子。在平衡状态下，费米能级（E_F）在整个结处都是均匀的。E_F位于结的p型侧的价带略上方，位于n型侧的导带略下方。

半导体p-n结在许多种电子器件中都很重要，包括二极管、晶体管、发光二极管和光伏电池。为了理解这些器件的工作原理，我们首先需要了解当我们将p型和n型半导体放在一起时，电子和空穴会发生什么变化。在两种材料之间的结处，移动的电子和空穴会相互湮灭，留下电子施主和电子受主掺杂剂的固定正电荷和负电荷。例如，在硅p-n结的n侧，带正电的掺杂剂是P⁺离子，而在p侧，带负电的掺杂剂是B^-。这些未补偿电荷的存在会产生一个电场，即p-n结的内建场。包含这些电荷（以及非常低密度的移动电子或空穴）的区域被称为耗尽区。

电场是由电子-空穴复合在耗尽区中产生的，它会将电子（在n侧）和空穴（在p侧）都排斥远离结点。然而，电子和空穴的浓度梯度倾向于通过扩散将它们移动到相反的方向。在平衡状态下，移动载流子的通量为零，因为场驱动的迁移通量与浓度驱动的扩散通量相等且方向相反。

耗尽层的宽度取决于半导体的屏蔽长度，而屏蔽长度又取决于掺杂剂的密度。在高掺杂水平下，耗尽层很窄（几十纳米），而在低掺杂密度下，它可以厚达1 µm。耗尽区是电场不为零的唯一地方，也是能带弯曲的唯一地方。在半导体的其他地方，电场为零，能带是平坦的。

在p-n结的中间，费米能级E_F位于价带VB和导带CB之间的一半，半导体是本征的（n = p = n_i）。

  10.6 二极管、LED和太阳能电池

二极管的近景，显示了方形半导体晶体（左侧黑色物体）。

二极管是一种半导体器件，它只允许电流在一个方向上流动。二极管在电子电路中充当整流器，也可以作为高效的发光器（在LED中）和太阳能电池（在光伏电池中）。二极管的基本结构是p型和n型半导体之间的结，称为p-n结。通常，二极管是由单个半导体晶体制成的，在该晶体中引入p型和n型掺杂剂。

如果二极管的n侧被偏置为正电位，而p侧被偏置为负电位，则电子被吸引到n侧，而空穴被吸引到p侧。这会增强p-n结的内建电位，耗尽区的宽度会增加，并且几乎没有电流流动。这种极化方向被称为“反向偏置”。如果二极管被偏置到另一个方向，载流子会被驱动到结点，在那里它们会复合。电场会减弱，能带会变平，并且电流会很容易流动，因为施加的偏置会降低内建电位。这被称为“正向偏置”。

正向偏置二极管中的电子（红色）和空穴（白色）。

二极管i-V曲线

左侧的图示说明了一个正向偏置的二极管，电流可以通过它轻松地流动。当电子和空穴被驱动到结点时（左下图中的黑色箭头），它们会复合（向下蓝色箭头），产生光和/或热。二极管中的费米能级表示为虚线。在耗尽区，费米能级有一个下降（等于施加的偏置）。相应的二极管i-V曲线显示在右侧。电流随着施加电压在正向偏置方向上呈指数级上升，而在反向偏置下几乎没有泄漏电流。在非常高的反向偏置下（通常为几十伏），二极管会发生雪崩击穿，并且会流过很大的反向电流。

发光二极管（LED）。

发光二极管或LED是一种二极管，它将电子-空穴复合的一部分能量转化为光。这种辐射复合过程总是与非辐射复合过程竞争，在非辐射复合过程中，能量只是转化为热量。当光从LED中发射出来时，光子的能量等于带隙能量。因此，与其他光源（如白炽灯和荧光灯）相比，LED灯具有纯净的颜色和窄的发射光谱。LED灯节能，因此通常摸起来凉爽。

直接带隙 半导体，例如 GaAs 和 GaP，具有高效的发光效率，并且也是良好的光吸收剂。在直接带隙半导体中，电子-空穴对的产生或复合过程中没有动量变化。也就是说，电子和空穴起源于动量波矢 k 的相同值，我们在第 6 章中遇到过。k 与动量（也是矢量量）相关，关系式为 p = hk/2π。在直接带隙半导体中，价带顶和导带底最典型地都出现在 k = 0 处。由于光子的动量接近于零，所以光子的吸收和发射是强烈允许的（因此动力学速度很快）。极性半导体，例如 GaAs、GaN 和 CdSe，通常是直接带隙材料。间接带隙 半导体，例如 Si 和 Ge，吸收和发射光的强度非常弱，因为价带最大值和导带最小值没有出现在 k 空间的同一点。这意味着还必须产生或湮灭晶格振动（声子）以守恒动量。由于这种“三体”（电子、空穴、声子）过程的概率很低，因此在间接带隙半导体中，电子和空穴的辐射复合速度比非辐射衰变（电子-空穴能量作为晶格振动的热化）慢。因此，动量选择规则阻止了光的吸收/发射，所以没有纯 Si LED 或 Si 基激光器。

虽然红、橙、黄、绿 LED 可以从 AlP-GaAs 固溶体中比较容易地制造出来，但最初制造蓝 LED 非常困难，因为带隙在合适能量范围内的最佳直接带隙半导体是一种氮化物 GaN，这种氮化物难以制造和掺杂为 p 型。日本日亚化学工业株式会社的 中村修二 成功开发了一种可制造的 p-GaN 制造工艺，这是蓝光 LED 的基础。由于这项工作在信息存储 (蓝光技术) 和全光谱、节能 LED 照明 的发展中的重要性，中村修二与 赤崎勇 和 天野浩 共享了 2014 年诺贝尔物理学奖，他们都曾在 GaN 二极管的开发中做出了早期贡献。

半导体 p-n 结中的光电效应。

一个 太阳能电池 或光伏电池，通过光电效应将 p-n 结中吸收的光直接转换为电能。光伏 是与开发用于将太阳能转换为电能的太阳能电池相关的技术和研究领域。有时太阳能电池一词专用于旨在专门捕获来自阳光的能量的装置，而光伏电池一词则用于光源未指定的情况。

太阳能电池在黑暗中和在带隙光照射下的电流-电压特性。短路光电流表示为 i_sc，开路光电压表示为 V_photo。太阳能电池产生的最大功率由橙色方框的面积决定。

p-n 结太阳能电池的等效电路，它产生了上图所示的“光” i-V 曲线。太阳能电池实际上是一个二极管，光产生的电子和空穴提供了反向偏置电流源。等效电路中的并联电阻 (R_sh) 代表寄生电子-空穴复合。为了获得高太阳能电池效率，需要高并联电阻（低复合率）和低串联电阻 (R_s)。

p-n 结太阳能电池中的光电流在二极管反向偏置方向流动。在黑暗中，太阳能电池只是充当二极管。在光照下，光电流可以看作是恒定电流源，它加在了二极管的 i-V 特性上。光伏电池的暗电流和光电流之间的关系如左图所示。

p-n 结的内建电场将由带隙光在耗尽区吸收而形成的 e^- h⁺ 对分离。电子向下流动，朝向结的 n 型侧，空穴向上流动，朝向 p 型侧。如果 hν ≥ E_gap，则光可以被吸收，从而将电子从价带提升到导带。任何多余的能量都会迅速热化。因此，具有 hν > E_g 的光只能在 e^- h⁺ 对中存储 E_g 的能量。如果光被吸收在耗尽区之外，即在没有电场的结的 n 型或 p 型侧，则少数载流子必须扩散到结中才能被收集。这个过程与电子-空穴复合过程竞争。由于杂质原子和晶格缺陷构成了有效的复合中心，因此用于太阳能电池的半导体（尤其是间接带隙材料，如 Si，为了吸收大部分太阳光谱，必须具有相对较厚的厚度）必须非常纯净。硅太阳能电池的大部分成本都与提纯元素硅和从熔体中生长大单晶的过程有关。

在上面的光电二极管 i-V 曲线中，V_photo 通常仅约为带隙能量 E_gap 的 70%。光电流受光子通量、复合率和吸收光的再发射限制。橙色矩形的面积表示太阳能电池产生的功率，可以计算为 P = i x V。在由 Si、GaAs、CdTe、CuIn_xGa_1-xSe₂ 或 (CH₃NH₃)PbI₃ 制成的优质单晶或多晶太阳能电池中，量子效率（短路光电流与光子通量的比值）接近于 1。

太阳能电池有许多当前应用。单个电池用于为小型设备供电，例如电子计算器。光伏阵列产生一种可再生电力，在电网电力无法获得的地方特别有用，例如偏远地区电力系统、绕地球运行的卫星和太空探测器、远程无线电话和抽水应用。光伏电力也越来越多地部署在并网电力系统中。

自 1976 年以来的 太阳能电池 能量转换效率的时间表 (美国国家可再生能源实验室)

过去十年中，安装光伏的成本（按每瓦计算）以每年约 13% 的速度下降，并且已经在德国和许多其他国家/地区达到 电网平价。预计光伏电网平价将在 2020 年左右在美国电力市场实现。 光伏电力成本不断下降的主要推动力是太阳能电池效率的稳步提高，如右图所示。更高效率的太阳能电池需要更少的面积来提供相同数量的功率，从而降低了“系统平衡”成本，例如布线、屋顶安装等，这些成本随着太阳能电池板面积的增加而增加。提高效率的进展反映了制造硅和砷化镓等光伏材料的改进工艺，以及新材料的发现。硅太阳能电池是一项成熟的技术，因此它们现在处于学习曲线的平坦部分，并且正在接近其最大理论效率。有机光伏、量子点太阳能电池和卤化铅钙钛矿电池等新技术仍然处于学习曲线的上升部分。

一个 场效应晶体管 (FET) 是一种使用电场来控制导电通道的宽度，从而控制半导体材料中电流的晶体管。它被归类为单极型晶体管，与 双极型晶体管 相反。

n 型 MOSFET 的横截面

场效应晶体管充当电流放大器。Si 基 FET 的典型结构是两个 n 型区域（源极和漏极）通过一个 p 型区域隔开。p 型区域上的氧化物绝缘体将金属栅极引线与半导体隔开。这种结构被称为 金属氧化物半导体 FET（或 MOSFET）。当在源极和漏极之间施加电压时，电流无法流动，因为要么 n-p 结或 p-n 结反向偏置。但是，当在栅极上施加正电位时，电子会被驱动到栅极，并且半导体局部“反转”为 n 型。然后，电流通过 n 型通道很容易地在 n 型源极和漏极之间流动。源极和漏极之间的电流流过栅极的电流要大得多，因此 FET 可以充当放大器。电流流动也可以表示逻辑“1”，因此 FET 也用于数字逻辑。

在微处理器等电子设备中，场效应晶体管在大多数时间都保持在关断状态，以最大程度地减少背景电流和功耗。上面所示的 FET，具有 n 型源极和漏极区域，被称为 NMOS 晶体管。在 PMOS 晶体管中，源极和漏极区域为 p 型，栅极为 n 型。在 CMOS（互补金属氧化物半导体）集成电路中，使用 NMOS 和 PMOS 晶体管。CMOS 电路以这样的方式构建，即所有 PMOS 晶体管必须从电压源或另一个 PMOS 晶体管接收输入。同样，所有 NMOS 晶体管必须从接地或另一个 NMOS 晶体管接收输入。这种排列导致低静态功耗。

晶体管在栅极电压范围内（如左图中的红色圆圈所示）最有用，在这个范围内，源极-漏极电流迅速变化。在这个区域，当在栅极上施加一个小信号时，可以使源极和漏极之间的电流发生较大变化。FET 的一个重要品质因数是 亚阈值斜率，它是 log(电流) 对 V_gate 图的斜率。理想的亚阈值斜率是每 60 mV 的栅极偏置变化一个数量级的电流。通常，可以实现源极-漏极电流的一个数量级的变化，栅极电压变化约 70 mV。FET 作为开关和放大器的性能受亚阈值斜率的限制，而亚阈值斜率又受栅极电容的限制。需要非常高的栅极电容，这需要薄的绝缘氧化物，但也需要很小的漏电流，这需要厚的氧化物。半导体行业当前面临的一个挑战是继续将 FET 缩放到更小的纳米级尺寸，同时保持这些参数的可接受值。这是通过开发具有比氧化硅更高的介电常数并且不会与硅或金属栅极引线发生氧化还原反应的新型栅极绝缘体材料来实现的。目前，只有少数已知材料（如氧化氮化铪和硅酸铪）才能满足这些严格的要求。

  10.7 非晶态半导体

结晶硅（左）、非晶硅（中）和氢化非晶硅（右）结构示意图

非晶半导体的能量与态密度图。无序和悬挂键导致局域化带隙态。

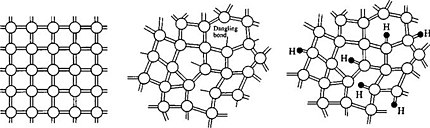
无定形半导体是结晶半导体材料的无序或玻璃态形式。与非导电玻璃一样，它们是主要由共价键连接的网络结构。结晶硅具有金刚石结构，是熔融的六元硅环的有序排列，所有环都处于“椅式”构象，正如我们在第 8 章中看到的。硅原子的局部键合环境是四面体。非晶硅（a-Si）中的硅原子也主要是四面体配位的，但结构中没有长程有序。除了六元环外，还有五元环和七元环，以及一些 Si 原子只有三个最近邻的“悬挂键”位点。

两种研究最广泛的无定形半导体是 a-Si 和非晶硒，a-Se。Si 和 Se 都可以制成玻璃态，通常是通过在相对较低的温度下溅射或蒸发。在 a-Se 中，与 a-Si 一样，在局部范围内，大多数原子都具有其“正常”价态，但结构中存在许多缺陷和不规则性。无定形半导体中的悬挂键在带隙中间具有轨道能级，这些状态中的电子实际上是非键合的。因为这些悬挂键位点彼此相距很远，所以它们之间的轨道重叠很小，并且它们也存在于一系列能量范围内。因此，这些带隙态中的电子是局域化的，这种现象被称为安德森局域化。非晶 Si 是绝缘体，因为费米能级（带隙中间）中的电子在晶格中不迁移。这些局域化态形成了迁移率间隙，只有在强烈键合或反键合态中的电子才是离域化的。因此，未经修饰的 a-Si 作为半导体并没有什么用。然而，通过在材料形成过程中进行氢化（通常在 H 原子等离子体中），欠配位的 Si 原子与氢原子键合。这会产生填充的键合轨道和空的反键合轨道，它们的能级位于迁移率间隙之外。因此，氢化降低了迁移率间隙中的态密度。氢化非晶硅 (a-Si:H) 在黑暗中是绝缘体，但却是良好的光电导体，因为光吸收会在迁移率间隙之外产生迁移的电子和空穴。

非晶 Se 的充电和静电复印循环中的图案内转移。

一台使用太阳能和电池供电的计算器

HIT 太阳能电池的层状结构。各层未按比例绘制。厚厚的结晶 n 型硅层是光吸收层，光生空穴（少数载流子）被那里的薄本征 a-Si 层反射远离铝背接触。

非晶 Se的光电导率被利用在静电复印中。用绝缘的 a-Se 涂覆的导电滚筒通过来自电线的电晕放电来充电。当滚筒暴露在明暗图案（要复制的图像）中时，照射的 a-Se 区域变得导电，滚筒上那些部位的静电荷会消散。然后，含碳的碳粉颗粒通过静电吸附到未暴露于光线的区域，并被转移并粘合到纸上以制作复印件。该过程的速度和图案内转移的高分辨率取决于 a-Se 在黑暗中的极低电导率和它在照射下的高电导率。

氢化非晶 Si用于廉价的薄膜太阳能电池。迁移率间隙约为 1.7 eV，大于结晶 Si 的带隙 (1.1 eV)。a-Si:H 是一种直接带隙材料，因此薄膜是良好的光吸收体。a-Si:H 太阳能电池可以以大面积薄片形式气相沉积。p⁺Si-a-Si:H-n⁺Si 电池的功率转换效率约为 10%。然而，非晶硅太阳能电池在暴露于光线下会逐渐降低效率。这种效率损失的机制，称为斯泰布勒-沃龙斯基效应，，涉及光生电子-空穴对，它们具有足够的能量引起材料的化学变化。虽然确切的机制尚不清楚，但有人提出电子-空穴复合的能量会破坏弱的 Si-Si 键，并且由此产生的悬挂键之一会夺取一个 H 原子，留下一个钝化的 Si-H 中心和一个永久的悬挂键。通过对 a-Si 进行氢化可以最大程度地减少这种影响，并且可以通过退火部分逆转这种影响。

薄层非晶硅与结晶硅一起用于异质结本征薄层 (HIT) 太阳能电池。 由于 a-Si 的迁移率间隙大于 c-Si 的带隙，因此在非晶-结晶界面处存在势能垒，该势能垒会将电子和空穴反射远离该界面。在 p⁺ 接触处，只有空穴才能通过势垒，而只有电子才能通过势垒到达 n⁺ 接触。对作为电子-空穴复合位点的表面缺陷的钝化，阻止了太阳能电池中的主要损失机制，从而提高了与传统的 c-Si p-n 结电池相比的光电压和光电流。松下和三洋已宣布生产功率转换效率高达 23% 的 HIT 电池。

  10.8 讨论问题

• 3d 过渡金属（Fe、Co、Ni）中的磁性有序和它们下方元素（Ru、Ir、Pd）中缺乏磁性与金属-绝缘体转变有何关系？
• 为什么好的金属是差的超导体，反之亦然？
• 讨论为什么早期过渡金属的半导体氧化物，如 TiO₂ 和 Nb₂O₅ 可以被 n 型掺杂，但不能被 p 型掺杂。相反，后期过渡金属氧化物的半导体氧化物，如 NiO 和 Cu₂O 可以被 p 型掺杂，但不能被 n 型掺杂。

  10.9 问题

1. 右侧显示了含有钡、铕、铜和氧的高温超导体的结构。该化合物中 Cu 的配位环境是什么？这种结构实际上与钙钛矿 ABO₃ 紧密相关。解释这种结构与理想钙钛矿结构之间的关系。

2. VO₂ 可以以绝缘体或金属形式存在，具体取决于温度和压力。哪种形式会因温度升高而稳定？解释你的答案。

3. 简要解释八隅体 p 区半导体的带隙如何以及为什么随 (1) 平均主量子数变化，以及 (2) 阴离子和阳离子之间的电负性差变化而变化。

4. 指出以下材料的导电类型（n 型或 p 型）：(a) Se 掺杂的 GaAs，(b) InAs_1-x，其中 x << 1，(c) Li_0.05Ni_0.95O，(d) Li_xWO₃，其中 x << 1。

5. 右侧以截面图显示了用于薄膜太阳能电池的铜铟硒半导体的结构。

(a) 该化合物的化学计量比是什么？

(b) 如果少量的碘取代硒，会发生哪种掺杂（n 型或 p 型）？

(c) 如果一小部分铟位点被铜原子占据，会发生哪种掺杂（n 型或 p 型）？

6. 带隙与吸收光波长之间的关系为 lambda (nm) = 1240/E_g (eV)。预测锐钛矿 TiO₂ (E_g = 3.1 eV)、SiC (2.0 eV)、ZnSnP₂ (1.7 eV)、ZnGeP₂ (1.9 eV) 和 InP (1.27 eV) 的颜色。换句话说，它们在人眼中呈现什么颜色？

7. 当温度从 300 K 升高到 330 K 时，某种本征（未掺杂）半导体的电导率增加了两倍。带隙（以 eV 为单位）是多少？R = 8.314 J/mol-K，1 eV/原子 = 96.52 kJ/摩尔。

8. 纯 Ge 的电导率远高于纯 Si。鉴于它们的带隙（分别为 0.74 和 1.15 eV），估计它们在室温下的电导率之比。

9. 右侧的图示显示了 Si、Ge 和 As 掺杂 Ge 的电导率与温度倒数的趋势。用合适的材料识别曲线 (i)、(ii) 和 (iii)。解释为什么曲线 (i) 的斜率接近于零。

10. 绘制一个硅 p-n 结，显示在没有光或外加电势的情况下，耗尽区、能带弯曲和费米能级。在黑暗中，p-n 结充当整流器。(a) 在黑暗中，电子和空穴最容易向哪个方向流动？(b) 内建电场在正向偏压下增加还是减少？(c) 在光线下，该结充当光电二极管。在这种情况下，在短路条件下，电子流向与 (a) 中相同还是相反？解释。