无机化学导论/离子型和共价型固体 - 能量学

第 9 章：离子型和共价型固体 - 能量学

在常压下，只有三种碱金属卤化物，CsCl、CsBr 和 CsI，采用 CsCl 结构。然而，在高压下，其他碱金属卤化物由于 CsCl 的 Madelung 常数较高，会从 NaCl 结构转变为 CsCl 结构。

在第 8 章中，我们学习了关于离子化合物的晶体结构。一个很好的问题是，是什么让化合物选择特定的结构？在解决这个问题时，我们将了解保持晶体结合在一起的力以及不同结构的相对能量。这将反过来帮助我们更定量地理解我们在前面章节中学习到的某些启发式概念，例如硬软酸碱理论。

第 9 章的学习目标

• 了解半径比规则的几何基础。
• 了解结构图的化学基础，以及为什么它们比半径比更能预测晶体结构。
• 使用 Born-Mayer 和 Kapustinskii 方程计算已知和假想化合物的晶格能。
• 使用晶格能构建 Born-Haber 循环，并计算循环中未知量。
• 使用晶格能预测低高氧化态的稳定性。
• 了解金属额外 "共振" 稳定性的量子力学起源。
• 使用晶格能预测无机化合物溶解度和热稳定性的趋势。

9.1 离子半径和半径比

晶体中的原子通过静电力、范德华力以及共价键结合在一起。因此，可以最大化这些吸引性相互作用强度的原子排列应该是最有利的，并导致最常见的观察到的晶体结构。

原子半径和离子半径。请注意，阳离子总是比同一元素的中性原子（粉红色）小，而阴离子更大。从元素周期表的任何一行从左到右，由于核电荷增加，中性原子和阳离子的尺寸都会缩小。（点击查看更大的图像）

半径比规则。早期的晶体学家在使用 X 射线衍射来解决无机固体的结构时遇到了麻烦，因为分析数据的某些数学工具尚未开发出来。一旦提出一个试探性结构，计算衍射图谱相对容易，但如果先验地对晶胞中原子的排列一无所知，则从衍射图谱推断出结构就很难了（而且至今仍然如此）。因此，开发一些关于猜测晶体中原子配位数和键合几何的准则至关重要（并且仍然至关重要）。第一个此类规则是由莱纳斯·鲍林提出的，他考虑了如何将不同半径的带相反电荷的球体堆积在一起。鲍林根据几何考虑，提出“匹配”的质量取决于阴离子和阳离子的半径比。

临界半径比。该图用于配位数 6：平面上的 4 个阴离子显示出来，1 个在平面上方，1 个在平面下方。稳定性极限在 r_C/r_A = 0.414 处

半径比规则的基本思想如右图所示。我们认为阴离子是晶体中的堆积原子，而较小的阳离子填充间隙位置（“孔”）。阳离子将在可以接触到最多数量的阴离子的排列中找到位置。如果阳离子可以接触到所有最近的邻近阴离子，如右图所示，对于与较大阴离子接触的小阳离子来说，那么匹配就很好。如果阳离子对于某个特定位置来说太小，那么该配位数将不稳定，并且它会更倾向于选择较低的配位结构。下表给出了对于特定配位几何形状给出最佳匹配的阳离子/阴离子半径比的范围。

配位数	几何形状	ρ = r阳离子/r阴离子
2	线性	0 - 0.155
3	三角形	0.155 - 0.225
4	四面体	0.225 - 0.414
4	平面正方形	0.414 - 0.732
6	八面体	0.414 - 0.732
8	立方体	0.732 - 1.0
12	立方八面体	1.0

不幸的是，使用这种思想来预测晶体结构存在几个挑战

• 我们不知道单个离子的半径
• 晶体中的原子并不真正是离子 - 存在不同程度的共价性，具体取决于电负性差异
• 键长（因此离子半径）取决于键强度和配位数（记住鲍林规则 D(n) = D(1) - 0.6 log n）
• 离子半径取决于氧化态（电荷越高 => 阳离子尺寸越小，阴离子尺寸越大）

我们可以通过假设键长是半径的总和（r₊ + r_-）来构建离子半径表，如果离子在晶体中接触的话。例如，考虑化合物 MgX 和 MnX，其中 X = O、S、Se。所有这些化合物都在 NaCl 结构中结晶

                      键长 (r_MX)

MgO  2.10      MgS  2.60      MgSe  2.73 Å

MnO  2.24      MnS  2.59      MnSe  2.73 Å

对于两个较大的阴离子（S^2- 和 Se^2-），两种阳离子的晶胞尺寸相同。这表明阴离子在这些结构中接触。从几何考虑，在这种情况下，阴离子半径由下式给出

$r_{-}={\frac {r_{MX}}{\sqrt {2}}}$

因此，S^2- 和 Se^2- 离子的半径分别为 1.84 和 1.93 Å。一旦确定了这些阴离子的尺寸，我们就可以从许多 MX 化合物的晶格常数获得一组自洽的阳离子和阴离子半径。

该模型效果如何？让我们考虑四价金属氧化物 (MO₂) 的结构，使用鲍林半径和半径比模型的预测

氧化物 MO2	半径比	预测的配位数	观察到的配位数（结构）
CO2	~0.1	2	2（线性分子）
SiO2	0.32	4	4（各种四面体结构）
GeO2	0.43	4	4（类似二氧化硅的结构）
"	0.54	6	6（金红石）
TiO2	0.59	6	6（金红石）
ZrO2	0.68	6	7（板钛矿）
"	0.77	8	8（萤石）
ThO2	0.95	8	8（萤石）

请注意，阳离子的半径取决于它们的配位数，因此对于配位数为 4 和 6 的 Ge⁴⁺ 以及对于配位数为 6 和 8 的 Zr⁴⁺ 计算出不同的半径比。

对于这系列氧化物，该模型似乎相当有效。在所有情况下，都预测了正确的配位数，并且像 GeO₂ 和 ZrO₂ 这样的临界情况在具有不同配位数的结构中被发现。该模型还正确预测了 BeF₂（SiO₂ 型）、MgF₂（金红石）和 CaF₂（萤石）的结构。

那么碱卤化物 NaCl、KBr、LiI、CsF 等呢？除了 CsCl、CsBr 和 CsI 具有 CsCl (8-8) 结构外，它们都具有 NaCl 结构。在这种情况下，半径比模型失效得很厉害。预测 Li⁺ 盐 LiBr 和 LiI 具有四面体结构，而 KF 预测具有与 CsCl 相似的 8-8 结构。我们可以尝试调整半径（例如，使阳离子更大，阴离子更小），但我们对碱卤化物所能做到的最好的结果是正确预测大约一半的结构。由于碱卤化物显然是离子化合物，这种失败表明半径比模型存在很大问题，它在 MO₂ 化合物中的成功是偶然的。

橄榄石的结构。M (Mg 或 Fe) = 蓝色球体，Si = 粉色四面体，O = 红色球体。

除了半径比规则外，莱纳斯·鲍林 还发展了其他有用的规则，这些规则有助于合理化并预测无机化合物的结构。鲍林规则 指出

• 稳定的结构是局部电中性的。例如，在双钙钛矿 Sr₂FeMoO₆ 的结构中，MO₆ (M = Fe²⁺, Mo⁶⁺) 八面体共享它们的所有顶点，而 Sr²⁺ 离子填充由八个 MO₆ 八面体包围的立方八面体空腔。 为了实现局部电中性，每个 O^2- 离子与一个 Fe²⁺ 和一个 Mo⁶⁺ 离子配位，因此 FeO₆ 和 MoO₆ 八面体在结构中交替出现。

• 阳离子-阳离子排斥应最小化。阴离子多面体可以共享顶点（如钙钛矿结构中）而没有任何能量损失。共享多面体边，特别是共享面，会导致阳离子-阳离子排斥，应该避免。例如，在金红石中，TiO₂ 的最稳定多形体，TiO₆ 八面体共享顶点和两个相对边，在结构中形成带。在锐钛矿 TiO₂ 中，每个八面体共享四个边，因此锐钛矿多形体在热力学上不太稳定。

• 高电荷阳离子在阴离子多面体中往往不共享边甚至顶点，尤其是在配位数较低的情况下。例如，在正硅酸盐（如橄榄石 (M₂SiO₄)）中，存在孤立的 SiO₄^4- 四面体。

正如我们很快将看到的那样，所有鲍林规则都可以在晶格能考虑的基础上得到证明。在离子化合物中，使阴离子-阳离子相互作用最大化，同时使阳离子-阳离子和阴离子-阴离子接触最小化的原子排列在能量上是最优的。

  9.2 结构图

结构图将结构与电负性等性质绘制在一起，在正确预测配位数和晶体结构方面比半径比规则更一致。这种方法的早期例子之一是由 Mooser 和 Pearson 在 1959 年发表的。

Mooser-Pearson 图根据原子的平均主量子数及其电负性差异来映射晶体结构。这种图背后的基本思想是

• 电负性差异越大，化合物越离子化。较高的离子性会导致较高的配位数，因为阴离子喜欢包围阳离子（反之亦然）。
• 较高的主量子数会导致更少的 s-p 杂化，更少的定向键合，因此配位数更高。我们之前在 IV 族元素的结构中看到了这种趋势：随着组的下降，配位数从 3-4 (碳) 逐渐增加到 12 (铅)。

Mooser-Pearson 图中的线将具有 CsCl、NaCl 和四面体（纤锌矿和闪锌矿）结构的 MX 化合物分开。请注意，在图中，纤锌矿的离子性高于闪锌矿，这与我们在第 8 章中讨论的“船”和“椅”环结构一致。二态性化合物往往落在边界上。总的来说，Mooser-Pearson 图在预测结构方面比半径比规则犯的错误要少得多。对于 MX₂ 结构也有类似的图，其中离子性的顺序为 CaF₂ (8:4 配位) > 金红石 (6:3) > 二氧化硅结构 (4:2)。

  9.3 晶体固体的能量学：离子模型

NaCl 晶体结构是计算晶格能和从 Born-Haber 循环计算生成焓的原型。

许多离子化合物具有简单的结构。由于使原子结合在一起的力主要是静电的，我们可以用良好的精度计算晶格的内聚能。关于这些晶格能计算，有趣的问题是

• 晶格能计算的精度如何？
• 它们告诉我们关于离子晶体中化学键的什么信息？
• 我们可以使用晶格能来预测溶解度、稳定性和反应性等性质吗？
• 我们可以使用晶格能来预测离子化合物的晶体结构吗？

让我们首先看看使离子晶格结合在一起的力。主要有两种类型的力决定了离子键的能量。

1) 静电力的吸引和排斥（库仑定律）：两个带电荷为 z₊ 和 z_- 的离子，相隔距离为 r，受到力 F 的作用

$\mathbf {F} =-{\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r^{2}}\qquad$

其中

e = 1.6022×10⁻¹⁹ C

4 π ε₀ = 1.112×10⁻¹⁰ C²/(J m)

对于异号离子，这种力是吸引力。

那么静电势能 E_elec 由下式给出

$\mathbf {E} _{elec}=\int _{\infty }^{r}F(r)\,\mathrm {d} r={\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r}.\qquad$

E_elec 的符号对于阳离子和阴离子之间的吸引相互作用为负。也就是说，相反带电离子相互靠近的距离越近，势能越低。

2) 闭壳排斥。当一个离子的闭合壳层中的电子与另一个离子的电子重叠时，会产生一种来自泡利不相容原理的排斥力。第三个电子不能进入已经包含两个电子的轨道。这种力是短程的，通常被模拟为随着原子间距离 r 的指数衰减或高次方衰减。例如，在玻恩近似中，B 是一个常数，ρ 是一个具有长度单位的数，通常从压缩性数据中经验确定。ρ 的典型值为 0.345 Å。

$\mathbf {E} _{repulsion}=B\exp \left({\frac {-r}{\rho }}\right).\qquad$

两个原子之间离子键的能量计算方法是，将净静电能和闭壳层排斥能结合起来，如图所示。注意，目前我们忽略了离子之间的范德华吸引能，我们将在下面解释。对于一对离子，离子之间的平衡距离由总能量曲线的最小值决定。在这个距离上，作用在每个离子上的净力为零。

马德隆常数是通过在扩展球体方法中对离子 0 与其他离子之间的静电相互作用进行求和而计算得出的。每个数字代表求和的顺序。例如，标记为 1 的离子表示六个最近邻（吸引力相互作用），标记为 2 的离子是接下来的 12 个最近邻（排斥力相互作用），等等。请注意，如果对壳层 1-2-3... 进行求和，则收敛速度非常慢，但有一些数学方法可以对它进行求和，从而得到快速收敛的级数。

晶格的静电能。我们可以使用这些方程通过对所有离子对之间的相互作用进行求和来计算晶体的晶格能。由于闭壳层排斥力是短程力，因此通常只对相邻离子之间的相互作用进行计算。然而，库仑力是长程力，必须在整个晶体上进行计算。这个问题最早由德国物理学家 埃尔温·马德隆 在 1918 年解决。^[4]

考虑右图中 NaCl 结构中标记为“O”的离子。我们可以看到，最近邻相互作用 (+ -) 与标记为“1”的离子之间是有吸引力的，而下一个最近邻相互作用 (- - 和 + +) 是排斥的，等等。在 NaCl 结构中，从晶胞中心的离子开始计数，有 6 个最近邻（在立方体的面上），12 个下一个最近邻（在立方体的边上），8 个在下一个壳层中（在立方体的顶点上），等等。它们与离子“0”的距离逐渐增加：r_o、√2 r_o、√3 r_o，等等，其中 r_o 是最近邻距离。

现在我们可以将离子“O”的静电能写成

$\mathbf {E} _{elec}=-6{\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r_{o}}+12{\frac {e^{2}}{4\pi \epsilon _{0}}}{\frac {z_{+}z_{-}}{{\sqrt {2}}r_{o}}}-8{\frac {e^{2}}{4\pi \epsilon _{0}}}{\frac {z_{+}z_{-}}{{\sqrt {3}}r_{o}}}+...$

将常数和最近邻键长 r_o 因式分解，我们得到

$\mathbf {E} _{elec}={\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r_{o}}\left(6-{\frac {12}{\sqrt {2}}}+{\frac {8}{\sqrt {3}}}-{\frac {6}{\sqrt {4}}}+\cdots \right)$

其中括号中的求和是无量纲的，它缓慢收敛到一个值为 A = 1.74756 的值。将此公式推广到任何三维离子晶体，我们得到一个函数

$\mathbf {E} _{elec}={\frac {e^{2}}{4\pi \epsilon _{0}}}{z_{+}z_{-} \over r_{o}}NA\qquad$

其中 N 是阿伏伽德罗常数（因为我们计算的是每摩尔离子的能量），A 被称为 马德隆常数。马德隆常数仅取决于离子的几何排列，因此它在不同类型的晶体结构之间变化，但在给定的结构类型内它不会改变。因此，MgO 和 NaCl 具有相同的马德隆常数，因为它们都具有 NaCl 结构。

下表列出了几种常见结构的马德隆常数。约化马德隆常数是通过将值归一化到化学式单元中的离子数量而得到的。从表中可以看出，不同结构的约化马德隆常数非常相似。这使得很难根据静电能计算来确定给定化合物最稳定的结构。有趣的是，约化马德隆常数的趋势大致遵循离子性的趋势（参见第 9.2 节中的 Mooser-Pearson 图）。例如，纤锌矿的马德隆常数略高于闪锌矿，这与我们之前的结论一致，即纤锌矿结构更受极性化合物的青睐。

结构	马德隆常数，A	约化马德隆常数，2A/n
NaCl（石盐）	1.7476	1.7476
CsCl	1.7627	1.7627
ZnS（闪锌矿）	1.6381	1.6381
ZnS（纤锌矿）	1.6413	1.6413
CaF2（萤石）	2.5194	1.6796
TiO2（金红石）	2.4080	1.6053
Al2O3（刚玉）	4.172	1.6688

氟化锂（这里显示为烧杯中的一块大的单晶体）是唯一一种不溶于水的碱金属卤化物。LiF 的晶格能是所有碱金属氟化物中最负的，因为 Li⁺ 和 F^- 都是小离子，而 E_L 与 1/r₀ 成正比。

晶体的总晶格能。现在我们有了静电能的公式，就可以加上闭壳层排斥项，得到一个可以给出总晶格能的方程。

$E_{L}={\frac {e^{2}}{4\pi \epsilon _{0}}}{\frac {z_{+}z_{-}}{r_{o}}}NA+NB\exp \left({\frac {-r}{\rho }}\right).\qquad$

在平衡键长处，所有离子的力都为零，我们可以利用这个事实来消除常数 *B*。

$\left[{\frac {dE}{dr}}\right]_{r=r_{o}}=0.\qquad$

由此，我们得到了Born-Mayer 方程。

$E_{L}={\frac {e^{2}}{4\pi \epsilon _{0}}}{\frac {z_{+}z_{-}}{r_{o}}}NA\left(1-{\frac {\rho }{r_{o}}}\right).$

这样表达，*E_L* 是一个负数（因为 z₊ 和 z_- 符号相反）。它代表从无限远处分离的一摩尔气态离子形成一摩尔固态盐的能量变化。

  9.4 NaCl 和卤化银的 Born-Haber 循环

现在我们有了离子晶体晶格能的方程式，我们可以问一个问题，它的准确性如何？记住，我们在推导出这个公式时做了一些近似。我们假设晶格是完全离子性的，忽略了离子的范德华吸引能，并假设键合中没有共价贡献。

让我们考虑食盐 (NaCl) 的晶格能。

Na⁺(g) + Cl^-(g) --> NaCl(s)

为了计算晶格能，我们将物理常数合并在一起。

$E_{L}(kJ/mol)=(1389.3){\frac {Az_{+}z_{-}}{r_{o}}}(1-{\frac {.345}{r_{o}}})$

其中 r_o 以 Å 为单位。现在我们可以使用 r_o = 2.814 Å 计算 NaCl 的晶格能，如

$E_{L}=-(1389.3){\frac {1.7476}{2.814}}(1-{\frac {.345}{2.814}})=-766.5$ kJ/mol

我们可以选择性地构建一个**Born-Haber 循环**，用于从元素形成 NaCl 并计算晶格能作为循环中“缺失的”项。

NaCl 的 Born-Haber 循环

S= Na(s) 的升华能

IP= Na(g) 的电离能

D= Cl₂(g) 的键解离能

EA= Cl(g) 的电子亲和能

E_L= NaCl 的晶格能

R= 气体常数

T= 绝对温度

根据**盖斯定律：** ΔH_f = S + 1/2D + IP + EA + E_L - 2RT = **-396 kJ/mol**

这里我们必须减去 2RT 将我们的能量循环转换为焓循环，因为我们在制造 NaCl(s) 时压缩了 2 摩尔气体，并且 PΔV = ΔnRT，其中 Δn = -2。

实验测得的 NaCl 的 ΔH_f 为 **-411 kJ/mol**

由于循环中的所有其他数字都是准确已知的，因此我们计算中的误差只有约 15 kJ（约为 E_L 的 2%）。这个结果很有希望，因为我们忽略了范德华项。

但是……我们如何才能忽略范德华项呢？

这是因为我们使用**能量最小化**来获得 Born-Mayer 方程中的排斥能。如果我们低估了晶格的吸引能，能量最小化准则确保排斥能也被低估。这两个误差部分抵消，因此计算中的总体误差很小。

我们可以通过明确包含离子之间的短程范德华吸引能来做得更好。下表显示了更详细的离子氟化物晶格能计算结果，其中明确包含了范德华项。在这种情况下，误差仅为 E_L 的约 1%。

化合物	计算的晶格能 (kJ/mol)	Born-Haber 循环得到的实验 EL
MgF2（金红石结构）	-2,920	-2,908
CaF2（萤石结构）	-2,586	-2,611
BaF2（萤石结构）	-2,326	-2,368

卤化银

一滴硝酸银溶液加入稀盐酸溶液中，会立即形成白色氯化银沉淀。此反应可用作溶液中卤化物离子存在的定性测试。AgCl、AgBr 和 AgI 的晶格能中共价键合的贡献使得这些盐在水中微溶。

对具有 NaCl 结构（AgF、AgCl、AgBr）或闪锌矿结构（AgI）的卤化银重复此练习很有趣。

卤化银	计算的	循环	差异 (kJ/mol)
AgF	-920	-954	34
AgCl	-833	-908	75
AgBr	-816	-900	84
AgI	-778	-883	105

从表中可以看出，AgF 的误差很小，而对于较重的卤化银，误差逐渐增大。然而，即使对于 AgI，我们仍然获得了大约 12% 误差内的答案。我们是否应该将与离子模型计算值的一致性解释为这些化合物是离子性的？显然，这种描述不适合 AgI，其中电负性差异 Δχ 仅为 0.6（将此值与 C-H 键的 0.4 相比较，我们通常将其视为非极性的）。

同样，我们可以将计算值与实验获得的能量之间偶然的一致性解释为补偿误差。我们的晶格能计算在较重的卤化银的情况下*高估了*离子贡献，但在*低估了*共价贡献。在这些化合物中，只有 AgF 可溶于水，应被认为是离子化合物。其他化合物在水中的溶解度逐渐降低（AgCl、AgBr 和 AgI 的 K_sp 分别为 10^-10、10^-13 和 10^-16），反映了随着 Δχ 减小共价性增加。

这个故事的寓意是，基于离子模型的简单晶格能计算效果很好，但*并不一定意味着这些化合物是离子性的*！

  9.5 Kapustinskii 方程

从上面的讨论可以清楚地看出，如果已知离子晶体的结构，则可以相当准确地计算其晶格能 E_L。但是，如果我们不知道未知结构的新化合物或假设化合物的结构，我们如何计算 E_L 呢？回想一下，不同的晶体结构的约化马德隆常数大致相同。俄罗斯化学家 A. F. Kapustinskii 认识到这一事实，并设计了一个公式，如果我们知道组成离子的单价半径，则可以计算任何化合物的 E_L。

马德隆常数 A 与化学式中离子的数量 (n) 成正比，因此将 A 除以 n 可以得到类似的值，如以下表格所示。

A/n ~ 不变

结构	A/n
NaCl	0.874
CsCl	0.882
金红石	0.803
萤石	0.800

卡普斯廷斯基注意到，M⁺ 和 M²⁺（单价与二价半径）之间离子半径的差异在很大程度上弥补了单价（NaCl，CsCl）和二价（金红石，CaF₂）结构之间 A/n 的差异。因此，他得到一个使用平均马德隆常数的晶格能公式，并将其修正为单价半径。在 卡普斯廷斯基公式 中，晶格能（kJ/mol）由以下公式给出。

$\mathbf {E} _{L}={1213.8z_{+}z_{-}n \over r_{+}+r_{-}}(1-{\frac {0.345}{r_{+}+r_{-}}})$

这里，单价半径之和用于代替 Born-Mayer 方程中的键长 r_o。这个公式的美妙之处在于它不需要任何关于化合物结构的知识。因此，它可以与 Born-Haber 循环相结合，来预测未知化合物的稳定性。正如我们将在下面看到的那样，这在指导合成和预测无机固体的反应性方面是一个广泛使用的工具。

  9.6 惰性气体化合物的发现

二氟化氙 (XeF₂) 的晶体，通过光解 Xe 和 F₂ 的气体混合物制得。XeF₂ 用作某些微电子制造工艺中 SiO₂ 的选择性蚀刻剂。在 1962 年尼尔·巴特利特发现第一个氙化合物之前，人们认为 VIII 族元素（He，Ne，Ar，Kr，Xe）不能形成化学化合物。从那时起，化学家们发现了包含 Xe、Kr 或 Ar 的丰富惰性气体化合物家族。

1962 年，在不列颠哥伦比亚大学，尼尔·巴特利特 研究强氧化剂 PtF₆，并且由于真空管线意外泄漏，他注意到该化合物与 O₂ 反应生成化学式为“PtF₆O₂”的固体。这个化学式表明 Pt 的氧化态为 +10，这显然是不合理的，因为已知 PtF₆ 比分子氟 (F₂) 或分子氧 (O₂) 都是更强的氧化剂。巴特利特注意到该化合物的 X 射线粉末衍射图谱与 Cs⁺AsF₆^- 的图谱相似，Cs⁺AsF₆^- 是一种具有 CsCl 结构的盐，其中八面体 AsF₆^- 离子占据氯离子位置。这促使巴特利特提出了一种新的化合物 O₂⁺PtF₆^- 的配方。 后来的磁化率数据证实了顺磁性 O₂⁺ 阳离子的存在，该阳离子（见第二章）的键级为 2.5。这种配方意味着 PtF₆ 是一种足够强的氧化剂，可以氧化分子氧。

但是 PtF₆ 的氧化能力到底有多强呢？可以使用 Born-Haber 循环估算其电子亲和力，并通过卡普斯廷斯基公式填入 O₂⁺PtF₆^- 的晶格能。



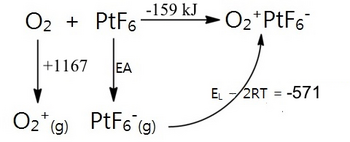
PtF₆ 的电子亲和力 (EA) 可以计算为 EA = -159 - 1167 + 571 = -751 kJ/mol。为了说明这一点，这比原子氟的电子亲和力 (334 kJ) 更放热 417 kJ/mol。PtF₆ 是迄今为止制备的最强氧化剂！

巴特利特认识到 Xe 的电离能为 +1170 kJ，与 O₂ 的电离能非常接近。由于 Xe⁺ 的大小应该与 O₂⁺ 相似，因此在 O₂⁺PtF₆^- 结构的阳离子位置使用 Xe⁺ 时，晶格能应该大致相同。由于 Xe 与 PtF₆ 反应的 Born-Haber 循环中的所有其他项都是相同的，因此巴特利特得出结论，Xe⁺PtF₆^- 应该像 O₂⁺PtF₆^- 一样是一种稳定的化合物。他买了一瓶氙气，并将这两种化合物反应，生成了橙色的固体。 虽然反应中最初形成的产物实际上可能是 Xe⁺PtF₆^-，但 Xe⁺ 自由基是一种强路易斯酸，会与过量的 PtF₆ 发生进一步反应。反应的最终产物被配制为 [XeF⁺][Pt₂F₁₁^-]，这是一种包含 Xe 的 +2 氧化态和 Pt 的 +5 氧化态的盐。这一发现非常重要，因为它打破了八隅体规则推断出的教条式观念，即 VIII 族元素不能与其他元素形成键。该组的名称从“惰性气体”改为“惰性气体”。随后，合成了许多 Xe 的化合物以及一些 Kr 和 Ar 的化合物（Ar 难以氧化得多），并对其进行了表征。

  9.7 高氧化态和低氧化态的稳定性

晶格能除了指导未知化合物的发现外，还有助于解释不存在的化合物的缺失（即热力学不稳定性）。 例如，CuF 和 AuF 是未知化合物，而 CuF₂、AuF₃ 和 AuF₅ 则是稳定的化合物。相反，AgF 是一种已知的稳定化合物。

从 CuF 的 Born Haber 循环来看，该化合物相对于元素来说应该是边缘稳定的（ΔH_f^o = -140 kJ/mol）。那么为什么 CuF 未知呢？

为了深入了解这个问题，我们首先构建一个从元素形成 CuF₂ 的 Born-Haber 循环。该化合物相对于元素来说是稳定的，为 -368 kJ/mol。

将两个循环组合起来，我们看到 CuF 的歧化成 Cu 和 CuF₂ 是自发的。从类似的循环中，我们还可以预测反应 3AuF → AuF₃ + 2Au 应该是自发的。

碘化亚铜 (CuI) 是一种在有机合成和人工降雨中使用的晶体化合物。这种化合物可以在实验室中通过将可溶性 Cu²⁺ 盐与碘化钠或碘化钾溶液反应制得。由于 CuI₂ 热力学不稳定，反应释放出 I₂，并形成 CuI 沉淀。

为什么这些氟化物的最低氧化态不稳定？关键是 E_L 值的巨大差异（铜氟化物的情况下为 2908-972=1926 kJ）驱动了它们的歧化反应。请注意，当我们使用卡普斯廷斯基方程时，我们计算出 CuF₂ 的 E_L 大致是 CuF 的三倍。我们在两个计算中使用相同的单价半径，但 Cu 在 CuF₂ 中的电荷为 2+（使晶格能相对于 CuF 翻倍），并且包含 3/2 个离子。因此，CuF₂ 的乘积 z₊z_-n 是 CuF 的三倍。因此，E_L 值的差异将随着单价盐的 E_L 增加而增加。我们知道，氟化物由于阴离子半径小，将比碘化物（阴离子半径较大）具有更大的 E_L 值。因此，对于 CuF 来说，歧化反应比对于 CuI 来说更有利。

因此，较低氧化态与较高氧化态的稳定性取决于阴离子的尺寸。例如，在氟化物中，CuF 不稳定，但 CuF₂ 稳定。然而，在碘化物中，CuI 稳定，而 CuI₂ 不稳定。由此我们可以得出广泛的结论：小的阴离子（O，F）倾向于稳定较高的氧化态，而大的阴离子（S，Br，I ...）倾向于稳定较低的氧化态。请注意，这种趋势与阴离子的尺寸有关，而不是与阴离子的电负性有关。巧合的是，F 和 O 是电负性元素，但实际上是它们的小尺寸对晶格能及其对较高氧化态的稳定性有影响。

请记住，硬软酸碱规则可以用离子相互作用与共价相互作用的优势来解释。在这里，我们将硬硬相互作用用（静电）晶格能进行了量化。

Ag 似乎违背了周期性趋势。为什么 AgF 稳定？这是因为它的第二电离能非常高（2071 kJ 对比 Cu 的 1958 kJ，Au 的 1979 kJ）。因此，AgF 和 AgF₂ 都是已知的 Ag 氟化物。

  9.8 碱金属负离子化合物和电子负离子化合物

电子负离子化合物中的空穴和通道

晶格能的另一个有趣的结果是，涉及包含 Na^- 和 e^- 阴离子的某些盐的形成。这些化合物分别被称为碱金属负离子化合物和电子负离子化合物。 这些化合物中的大多数是由密歇根州立大学的詹姆斯·戴教授发现的。

碱金属在其价层中只有一个电子。例如，Na 和 K 的电子构型分别为 [Ar]3s¹ 和 [Kr]4s¹。虽然我们习惯于看到这些非常电正的元素在与电负性元素形成化合物时失去它们的电子，但它们也可以获得一个电子以达到 [惰性气体]ns² 构型。这在强电子给予体（如碱金属）中是可能的，尤其是当形成的阳离子通过与冠醚配位而得到稳定时。通常，这些化合物通过将碱金属和合适的冠醚在液氨中混合，然后蒸发氨来合成。

电化物盐在类似条件下形成，只是在这种情况下，阴离子只是一个存在于晶体中阴离子“空腔”中的电子。晶体结构明显类似盐，阳离子（被冠醚或穴醚配体稳定的碱金属阳离子）在结构中与电子交替排列。

18-冠-6，一种与Na⁺ 阳离子强烈络合的冠醚

用冠醚配体络合Na⁺（K⁺，Rb⁺，Cs⁺）可稳定金属的M⁺形式（“盐”形式）。由于金属阳离子和其配体壳层相当大，因此这些盐的晶格能相当低。

电化物盐的溶液是强还原剂，如它们在Birch 还原中的应用所示，其中芳香族化合物被氢化生成二烯烃。电化物也可用於将金属离子还原成金属。在无水氨中蒸发蓝色电化物溶液会产生钠的镜面。随着电子将氨还原成酰胺阴离子，这些溶液会慢慢失去颜色

[Na(NH₃)₆]⁺e⁻ + NH₃ → NaNH₂ + H₂

在晶格能和玻恩-哈伯循环的背景下，考虑一下如果不存在这些配体会发生什么。也就是说，我们可以问一个问题，即钠金属是否更喜欢以金属形式 Na(s) 存在，还是形成 sodide 盐 Na⁺Na^-，或形成电化物盐 Na⁺ e^-。当然，我们已经知道这个问题的答案。元素钠显然是一种金属（它有光泽、导电，并具有体心立方晶体结构），从未在任何一种“盐”形式中被观察到。但这些形式在能量上相距多远呢？

我们可以通过假设 Na- 离子的大小与 Br^- 相当，e^- 阴离子的大小与 Cl^- 相当来计算能量学。然后循环中的晶格能就与 NaBr 和 NaCl 的晶格能相同

这些计算得出的相当令人惊讶的结果是，钠作为 sodide 盐将是微弱稳定的，并且作为电化物将非常稳定（161 kJ）。这些简单循环中的所有项都是精确已知的。但是我们在这里一定做错了什么，因为 Na(s) 显然是金属。

这里关键的、微妙的点是，玻恩-哈伯循环只考虑循环中物质的势能（而不是总能量）。通常，我们可以忽略总能量中的动能部分，但在这种情况下，我们不能，因为存在共振的量子力学效应。

  9.9 金属的共振能

钠的金属特性归因于其离域价电子的共振稳定。

上述问题的解决方案必须考虑电子的量子力学性质。钠金属中的价电子处于遍布整个晶体的离域轨道中。然而，在 Na⁺ e^- “盐”形式中，电子被定位在特定的阴离子位点上。这种定位赋予了额外的动能（通过“盒子中的粒子”效应），从而增加了总能量。从盒子中一维粒子的量子力学结果中，我们得到

$KE={\frac {h^{2}n^{2}}{8mL^{2}}}$
其中

h = 普朗克常数 = 6.626 x 10^-34 J s

n = 能级，假设为最低能级，n = 1

m = 电子质量 = 9.109 x 10^-31 kg

L = 盒子的大小

如果我们将电子“盒子”的大小近似为 3 Å（3 x 10^-10 m），我们得到

$KE={\frac {(6.626\cdot 10^{-34})^{2}(6.022\cdot 10^{23})}{8\cdot (9.1\cdot 10^{-31})(3\cdot 10^{-10})^{2}}}=4.04\cdot 10^{5}J/mol=+404kJ/mol$

这种额外的动能使 Na⁺e^- “盐”相对于电子离域金属不稳定。

该计算并不十分准确，因为金属中电子的动能不为零，并且因为“盒子”的大小没有得到很好的定义。然而，它确实说明了电子离域对热力学稳定金属具有重大影响。这种情况与芳香族分子通过电子离域稳定完全类似。在苯等分子中，共振也是一种量子力学动能效应。一般来说，金属中的共振稳定能明显大于π-离域有机分子中的共振稳定能。例如，苯中六个π电子的共振能约为 151 kJ/mol，不到我们在钠金属中计算的（每个电子）值的一半。

Ca₂N 的晶体结构，蓝色示意性地显示了二维电子层。

有趣的是，几种碱金属（和其他金属元素）在超高压下转变为光学透明的绝缘相，其中价电子被定位。 这些高压电化物相违背了一般规律（我们将在第 10 章中遇到），即绝缘体在足够高的密度下会转变为金属。它们说明了元素的稳定结构如何取决于离子电化物结构的晶格能与电子离域金属的共振能之间的权衡。

除了通过使碱金属与冠醚配体络合而形成的类似盐的电化物之外，最近还发现了一些固态氮化物和氧化物，例如 Ca₂N 和 Ca₂₄Al₂₈O₆₄，它们更准确地被表述为电化物，即 [Ca₂N⁺](e^-) 和 [Ca₂₄Al₂₈O₆₄]⁴⁺(e⁻)₄. 在这些化合物中，Ca、Al、O 和 N 原子具有其通常的八隅体氧化态（分别为 +2、+3、-2 和 -3），电子充当阴离子，填充晶体中笼状空隙或层。例如，Ca₂N 采用反 CdCl₂ 结构，如右侧所示，层间存在空隙，这些空隙被二维电子气体占据。与其他层状材料一样，Ca₂N 可以轻松地剥落成薄纳米片，同时保留其作为电化物的结构和特性。 这些化合物是强还原剂，并且还具有有趣的催化活性。

  9.10 碱金属氧化物的奇怪案例

钠金属在空气中被氧化成过氧化钠 Na₂O₂

K₂O（上）和Cs₂O（下）晶体结构的空间填充模型。氧原子为红色，钾离子为蓝色，铯离子为品红色。

意外的化学计量。碱金属氧化物，由碱金属（Li、Na、K、Rb、Cs）与氧气反应制得，呈现出一种不寻常的趋势。当锂与氧气反应时，我们得到二元氧化物Li₂O，这与第一族元素与第六族元素的结合预期一致。奇怪的是，钠金属氧化时最容易形成的氧化物不是Na₂O，而是过氧化物Na₂O₂，我们可以将其表示为(Na⁺)₂(O₂^2-)。对于钾、铷和铯，我们得到超氧化物MO₂，其中含有超氧化物自由基阴离子(O₂^-.)，应该表示为(M⁺)(O₂^-)。虽然可以通过适当的金属硝酸盐(MNO₃)与元素碱金属M反应来制备Na₂O、K₂O、Rb₂O和Cs₂O， 但奇怪的是，这些“正常价”化合物不会通过金属与氧气的直接反应而形成。

由于碱金属都具有很强的电正性（χ = 0.8-1.0），而氧气具有很强的电负性（χ = 3.5），因此我们预计所有通过将它们组合而成的化合物都是可靠的离子化合物。与这种图景一致，我们发现Li₂O（以及Na₂O、K₂O和Rb₂O）采用反萤石结构（8:4 配位 - 见问题 8.8.2），我们预计会发现相对离子性的M₂X 化合物。然而奇怪的是，Cs₂O 在反CdCl₂ 结构中结晶。这很奇怪，因为CdCl₂ 具有层状结构，我们通常将其与极性共价MX₂ 化合物相关联（见第 8.4 节）。在Cs₂O 中，六个Cs⁺ 阳离子以八面体形式包围每个O^2- 阴离子。每个Cs⁺ 与三个O^2- 离子配位，Cs⁺ 离子在范德华间隙中相互接触。Cs⁺ 离子彼此靠近显然在静电上是不利的，那么为什么Cs₂O 更喜欢反CdCl₂ 结构而不是反萤石结构呢？

答案与碱金属离子围绕氧的拥挤有关，如右图所示的K₂O。由于八个较大的K⁺ 离子包围每个O^2- 离子，因此阳离子基本上是相互接触的。实际上，在Na₂O、K₂O 和Rb₂O 中，金属-氧键相对于其他结构中具有相同键序的M-O 键而言是“拉伸”的。 Cs₂O 的情况非常极端，因此它找到了一种（静电上不利的）结构，其中配位降低为 6:3。这种堆积问题在过氧化物中得到一定程度的缓解，在过氧化物中配位仍然是 8:4，但阴离子更大，特别是在超氧化物中，阳离子：阴离子比率为 1:1，配位为 6:6。因此，较大的碱金属离子（K⁺、Rb⁺、Cs⁺）倾向于形成超氧化物。

我们可以通过形成氧化物、过氧化物和超氧化物的能量学来解释这种趋势的另一种方法。

让我们计算一下从金属和氧气形成金属氧化物M₂O（每摩尔金属）的焓变。

M(s) + 1/4 O₂(g) --> 1/2 M₂O(s)

我们可以使用赫斯定律将其写成反应的总和

反应	ΔH
M(s) --> M(g) --> M+(g)	ΔHs + IE = ΔHf,M+(g)
1/4 O2(g) --> 1/2 O(g) --> 1/2 O2-(g)	1/4 ΔHd + 1/2 EA1 + 1/2 EA2 = 1/2 ΔHf,O2-(g)
M+(g) + 1/2 O2-(g) --> 1/2 M2O(s)	1/2 EL,M2O - 3/2 RT
总计
M(s) + 1/4 O2(g) --> 1/2 M2O(s)	ΔHf,M+(g) + 1/2 ΔHf,O2-(g) + 1/2 EL,M2O - 3/2 RT

为了得到总反应的焓变（1/2 摩尔 M₂O 的生成热），我们需要M⁺(g) 和O^2-(g) 的生成热，这些热值可以从表格中获得，以及E_L，我们可以用卡普斯廷斯基方程计算。

类似地，我们可以写出碱金属过氧化物的形成

M(s) + 1/2 O₂(g) --> 1/2 M₂O₂(s)

反应	ΔH
M(s) --> M(g) --> M+(g)	ΔHf,M+(g)
1/2 O2(g) --> 1/2 O22-(g)	1/2 ΔHf,O22-(g)
M+(g) + 1/2 O22-(g) --> 1/2 M2O2(s)	1/2 EL,M2O2 - 3/2 RT
总计
M(s) + 1/2 O2(g) --> 1/2 M2O2(s)	ΔHf,M+(g) + 1/2 ΔHf,O22-(g) + 1/2 EL,M2O2 - 3/2 RT

以及超氧化物

M(s) + O₂(g) --> MO₂(s)

反应	ΔH
M(s) --> M(g) --> M+(g)	ΔHf,M+(g)
O2(g) --> O2-(g)	ΔHf,O2-(g)
M+(g) + O2-(g) --> MO2(s)	EL,MO2 - 2 RT
总计
M(s) + O2(g) --> MO2(s)	ΔHf,M+(g) + ΔHf,O2-(g) + EL,MO2 - 2 RT

对于气态阴离子和阳离子，我们有以下生成热和离子半径（CN=6）

离子	ΔHf, kJ	离子半径，Å
Li+	678	0.76
Na+	602	1.02
K+	506	1.38
Rb+	485	1.52
Cs+	473	1.67
O2-	500	1.20
O22-	519	1.59
O2-	-88	1.49

现在使用卡普斯廷斯基方程，我们可以计算出每种化合物的晶格能；这些晶格能已通过减去 2 RT 或 3 RT（根据需要）转换为晶格焓

$\mathbf {E} _{L}={1213.8z_{+}z_{-}n \over r_{+}+r_{-}}(1-{\frac {0.345}{r_{+}+r_{-}}})$

金属	ΔHL,M2O	ΔHL,M2O2	ΔHL,MO2
Li	-3,065 kJ	-2,651 kJ	-918 kJ
Na	-2,776	-2,433	-838
K	-2,454	-2,178	-751
Rb	-2,345	-2,090	-721
Cs	-2,241	-2,007	-678

正如预期的那样，M₂O 和M₂O₂ 的晶格能相当，后者的大小略小一些，因为O₂^2- 阴离子的尺寸更大。超氧化物MO₂ 的晶格能大约是相应过氧化物晶格能的 1/3，因为阴离子和阳离子都是单电荷的，并且每个化学式单位中只有两个离子。

现在，将所有这些放在一起，我们可以使用晶格能和单个离子的生成热来比较每种氧化物的生成热（每摩尔金属）

金属	1/2 ΔHf,M2O	1/2 ΔHf,M2O2	ΔHf,MO2
Li	-404 kJ	-388 kJ	-328 kJ
Na	-338	-354	-324
K	-271	-321	-328
Rb	-241	-300	-324
Cs	-53	-70	-81

我们可以看到，对于Li，Li₂O 的形成优于Li₂O₂ 或LiO₂，因为Li₂O 的晶格能非常有利。随着晶格能随着阳离子尺寸的增加而变得越来越不负，过氧化物在Na处变得最稳定。对于较重的碱金属，M₂O 变得很不稳定，超氧化物MO₂ 最稳定。这与我们对第一族氧化物化学性质的观察结果一致。

Rb₉O₂ 簇在Rb 次氧化物中

碱金属次氧化物。有趣的是，最重的碱金属（Rb、Cs）也形成一系列次氧化物，例如Rb₉O₂、Rb₆O、Cs₁₁O₃、Cs₄O、Cs₇O、Cs₁₁O₃Rb、Cs₁₁O₃Rb₂ 和Cs₁₁O₃Rb₃，其中氧化物离子被碱金属以八面体形式配位。富含金属的化学计量（例如，Rb₆O 和Cs₇O）是这些簇与碱金属的晶体共生。 这些化合物是有效的还原剂。

呼吸空气锂电池示意图

金属-空气电池。碱金属氧化物在金属-空气电池的背景下非常有趣，因为它们在质量基础上具有极高的储能潜力。此类电池具有碱金属（通常为 Li）或 Zn 负极，并在正极利用空气中的氧气。虽然锂是最轻的，因此也是能量密度最高的碱金属，但在电池充电时，与锂枝晶的形成以及正极上O₂(g) 和2 O^2- 之间四电子相互转化的缓慢动力学有关的材料问题。出于这个原因，目前正在研究超氧化物电池作为替代方案。单电子正极反应O₂ + e^- = O₂^- 的动力学很快，钾 和钠 代表了这些呼吸空气电池负极锂的潜在可行替代品。最近，已经证明LiO₂ 可以通过在铱纳米粒子上的模板生长而动力学稳定，这有可能为非常高能量密度的锂空气电池打开大门。

  9.11 晶格能和溶解度

晶格能也可以帮助预测化合物溶解度。让我们考虑一下将盐溶解在水中的玻恩-哈伯循环。我们可以将其想象成两个过程的总和：（1）盐汽化以产生气态离子，以晶格焓为特征，以及（2）这些离子的水合作用以产生溶液。整个过程的焓变是这两个步骤的总和。我们知道固体溶解的熵变是正的，因此溶解度取决于整个过程的焓变。

这里我们需要考虑晶格能 E_L 和水合能 E_H 的趋势。晶格能取决于阴离子和阳离子半径之和 (r₊ + r_-)，而水合能则有单独的阴离子和阳离子项。一般来说，由于 1/r² 依赖性，小离子（通常是阳离子）的溶剂化占主导地位。

$E_{L}\propto {\frac {1}{r_{+}+r_{-}}}$

$E_{H}\propto {\frac {1}{r_{+}^{2}}}+{\frac {1}{r_{-}^{2}}}$

对于含有较大阴离子的盐，当 r₊ 变化时，E_L 不会发生太大变化。这是因为阴离子在 E_L 公式的分母中的 r₊ + r_- 项中占主导地位。另一方面，E_H 随着 r₊ 的变化而发生显著变化，特别是对于小的阳离子。

因此，小的二价阳离子的硫酸盐，如 MgSO₄（泻盐），是可溶的，而 BaSO₄ 中 Ba²⁺ 的水合能较低，使得该盐不溶（K_sp = 10^-10）。

左图：硫酸盐的 E_L 图。大的 SO₄^2- 离子与小的阳离子（如 Mg²⁺）的大小不匹配，这些阳离子的水合能很高，从而形成可溶性盐。对于较大的阳离子（如 Ba²⁺），其 E_H 较低，晶格能超过溶剂化焓，因此盐不溶。右图：在小阴离子（如 F^- 和 OH^-）的情况下，晶格能与小的阳离子（如过渡金属离子 (TMⁿ⁺)、Mg²⁺ 和 Li⁺）占主导地位。阴离子和阳离子的大小不匹配发生在较大的阳离子（如 Cs⁺ 和 Ba²⁺）中，这些阳离子会形成可溶性氟化物盐。

对于小的阴离子，E_L 对 r₊ 更敏感，而 E_H 对 r₊ 的依赖性不那么强。对于氟化物和氢氧化物，LiF 稍微可溶，而 CsF 非常可溶，Mg(OH)₂ 不溶，而 Ba(OH)₂ 非常可溶。

将这两种趋势结合起来，我们发现，低溶解度最常出现在阴离子和阳离子在尺寸上良好匹配的情况下，特别是当其中一个或两个都具有多重电荷时。

空间填充模型显示了 Ba²⁺ 和 SO₄^2- 的范德华表面。两种离子的尺寸相似有助于 BaSO₄ 在水中的低溶解度。

结合我们对溶解度的所有结论，我们注意到以下趋势

1) 阴离子和阳离子之间的尺寸不匹配增加会导致更高的溶解度，因此 CsF 和 LiI 是碱金属卤化物中最可溶的。

2) 共价性增加会导致盐的溶解度降低（由于 E_L 更大）。例如，AgF、AgCl、AgBr 和 AgI 的溶解度逐渐降低，因为共价性增加。

AgF > AgCl > AgBr > AgI

3) 阴离子电荷增加会导致溶解度降低，因为 E_L 的增加相对于 E_H 的增加较大。

4) 小的、多价阳离子（具有较大的 E_H）会与大的、单价阴离子形成可溶性盐，如 I^-、NO₃^-、ClO₄^-、PF₆^- 和乙酸根。

例子：过渡金属和镧系元素离子的盐

• Ln³⁺：硝酸盐可溶，但氧化物和氢氧化物不溶。

• Fe³⁺：高氯酸盐可溶，但硫酸盐不溶。

5) 多重电荷阴离子，如 O^2-、S^2-、PO₄^3- 和 SO₄^2-，会与大多数 M²⁺、M³⁺ 和 M⁴⁺ 金属形成不溶性盐。

  9.12 讨论问题

• 解释为什么晶格能计算对于 NaCl 和 CaCl₂ 非常准确，但对于 AgCl 和 PbCl₂ 却不太准确（大约 10%）。Born-Mayer 方程是否低估或高估了后者的值？
• 氟的电负性比氧更高。然而，对于许多过渡金属，我们可以在氧化物中形成比在氟化物中更高的氧化态。例如，Mn(IV) 在氧化物 (MnO₂) 中是稳定的，但 MnF₄ 相对于 MnF₃ 和氟是不稳定的。^[22] 你能用晶格能来解释这一点吗？

  9.13 问题

1. 利用晶格能解释为什么 MgSO₄ 在比 BaSO₄ 低得多的温度下分解成氧化镁和 SO₃。

2. 当钠金属被氧化时，最容易形成的氧化物不是 Na₂O，而是过氧化物 Na₂O₂，我们可以将其表示为 (Na⁺)₂(O₂^2-)。钙离子的电负性 (1.0) 和离子半径 (1.14 Å) 非常接近钠的电负性 (0.9) 和离子半径 (1.16 Å)。你认为钙暴露在空气中会形成氧化物 (CaO) 还是过氧化物 (CaO₂)？解释你的推理。

3. 固体 CaO 可以表示为 Ca⁺O^- 或 Ca²⁺O^2-。使用下面的热化学数据（其中一些与问题无关）和 Kapustinskii 公式来确定哪种更稳定。CaO 的晶格常数（NaCl 结构）为 4.810 Å。虽然 O^- 离子的想法可能看起来很奇怪，但请注意，O 的第二次电子亲和能和 Ca 的第二次电离势（在下表中）都是相当吸热的。

反应	∆Ho，kJ/mol
Ca(s) = Ca(g)	178
Ca(g) = Ca+(g) + e-	590
Ca+(g) = Ca2+(g) + e-	1,145
O2(g) = 2 O(g)	498
O(g) + e- = O-(g)	-141
O-(g) + e- = O2-(g)	790

4. 从固体 NH₄Cl 的生成热 (-315 kJ/mol) 和气态 NH₃ 的生成热 (-46)、H₂ 的键解离能 (436) 和 Cl₂ 的键解离能 (244)、原子氢的电离势 (1,311) 和原子氯的电子亲和能 (-349) 中，计算 NH₃ 的气相质子亲和能。NH₄Cl 的晶格能可以通过 Kapustinskii 公式估计，使用 r_N-Cl = 3.50 Å。

5. 氨水瓶通常标注为“氢氧化铵”。我们将通过使用晶格能计算来检验这一观点，以确定 NH₄⁺OH^- 盐是否可以存在。

气态 OH- 和 H₂O 的生成热分别为 -141 和 -242 kJ/mol。假设 NH₄⁺ 的大小与 Rb⁺ 相似，而 OH^- 的大小与 F^- 相似，使用 Kapustinskii 公式、离子半径和问题 4 中计算的 NH₃ 质子亲和能，确定 NH₄⁺OH^- 相对于 NH₃ 和 H₂O 是否应该是一种稳定的盐。在什么温度下 NH₄⁺Cl^- 相对于 NH₃ 和 HCl 应该是不稳定的，如果 HCl 的 ΔH_f^o 为 -92 kJ/mol，而 ΔS^o (NH₄Cl --> NH₃ + HCl) = 280 J/mol K？

6. 锂金属在氮气中燃烧生成氮化锂 Li₃N。较重的碱金属 (K、Rb、Cs) 可以形成稳定的叠氮化物 (MN₃)，但不能形成 M₃N 氮化物。解释为什么是这样。

7. (a) 你认为 BaSO₄ 还是 MgSO₄ 在水中的溶解度更高？(b) LiF 的溶解度是否高于 LiClO₄？解释。

8. 你认为 ZnS 的哪种多晶型（闪锌矿或纤锌矿）在静电能方面更稳定？

9. 地下水中的砷污染是孟加拉国、智利、阿根廷以及美国西部等世界各地的一个严重问题。在恒河三角洲，砷中毒十分普遍，因为抽水机从地下 20-100 米处抽取受污染的水。人们提出的一种简单的处理方法是通过对井水进行曝气来沉淀砷，井水中也含有高浓度的 Fe²⁺。参考右侧的砷 Pourbaix 图和第 4 章中铁的 Pourbaix 图，确定在中性 pH 下曝气水中存在的铁和砷物种。什么不溶性化合物会沉淀下来以降低砷的浓度？(提示：哪种化合物的晶格能最大？)