无机化学导论/分子轨道理论

第2章：分子轨道理论

一氧化碳分子中最低未占分子轨道是一个 π 反键轨道，它来自碳（左）和氧（右）的 2p 轨道

价键理论（VB）为我们提供了化学键合的定性图像，这对于预测分子形状、键强度等非常有用。它不能准确描述一些键合情况，因为它忽略了电子的波动性。

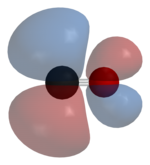
分子轨道理论（MO）具有更定量的潜力。利用它，我们还可以获得电子在分子中的位置图像，如右侧图像所示。这可以帮助我们理解其他难以解释的键合和反应模式。

尽管 MO 理论原则上为我们提供了一种非常精确地计算电子在分子中的能量和波函数的方法，但通常我们也采用简化的模型。这些简单模型并没有给出非常精确的轨道和键能，但它们确实解释了共振等概念（例如，在二茂铁分子中），这些概念在其他情况下难以表示。我们可以通过计算“数值计算”从 MO 理论获得更精确的能量。许多商业和开源的程序已经开发出来，用于精确计算分子和扩展固体的电子结构。

虽然 MO 理论比 VB 理论更正确，并且可以非常准确地预测分子的性质，但即使对于相当简单的分子，它也相当复杂。例如，你应该毫不费力地画出 CO、NH₃ 和苯的 VB 图像，但我们会发现，随着 MO 理论的发展，这些图像会越来越具有挑战性。

第 2 章的学习目标

• 能够为同核双原子、异核双原子、同核三原子和异核三原子分子构建分子轨道图。
• 理解并能够阐明分子轨道形成的方式——概念上、视觉上、图形上和（半）数学上。
• 将双原子和三原子分子的键序、键长和键强度联系起来，包括中性形式和离子形式。
• 利用分子轨道理论预测简单三原子体系的分子几何形状。
• 根据轨道重叠和键合，合理化几个特定体系的分子结构。
• 理解具有 π 键合的分子中芳香性和反芳香性的起源。

  2.1 从原子轨道构建分子轨道

分子轨道理论涉及（近似地）求解分子中电子的薛定谔方程。回顾第 1 章，这是一个微分方程，其中右侧的第一项和第二项分别代表动能和势能。

$E\psi =-{\frac {\hbar ^{2}}{2\mu }}\nabla ^{2}\psi +V\psi$

虽然薛定谔方程可以针对氢原子进行解析求解，但当分子中存在多个（相互排斥）电子时，势能函数 V 会变得更加复杂——然后方程只能进行数值求解。因此，作为第一个近似值，我们将假设构成分子的原子的 s、p、d、f 等轨道是薛定谔方程的良好解。然后，当我们将原子结合在一起形成键时，我们可以允许这些波函数发生相长和相消干涉。这样，我们利用原子轨道（AO）作为构建 MO 的基础。

LCAO-MO = 原子轨道线性组合。 在物理学中，这被称为紧束缚近似。

我们实际上以前在第 1 章构建杂化轨道时就见过原子轨道的线性组合。我们为杂化开发的基本规则也适用于这里：轨道以标量系数 (c) 相加，使得所得轨道是正交的和归一化的。不同之处在于，在 MO 情况下，原子轨道来自不同的原子。

原子轨道的线性组合总是返回相同数量的分子轨道。因此，如果我们从两个原子轨道开始（例如，一个 s 和一个 p_z 轨道，如图 2.1.1 所示），我们最终会得到两个分子轨道。当原子轨道同相相加时，我们得到相长干涉和较低能量的轨道。当它们反相相加时，我们得到一个节点，所得轨道具有更高的能量。较低能量的 MO 是成键的，较高能量的 MO 是反键的。

图 2.1.1。s 和 p 轨道的 σ 成键和反键组合

图 2.1.2。内皮细胞的不同成分用蓝色、绿色和红色荧光染料染色。对于每种染料，发射光的颜色对应于电子从分子的 LUMO 降至 HOMO 时释放的能量。

分子轨道也称为波函数（ψ），因为它们是分子薛定谔方程的解。原子轨道（也称为基函数）标记为 φ，例如，φ_1s 和 φ_3pz 或简称为 φ₁ 和 φ₂。

原则上，我们需要针对分子中的所有轨道求解薛定谔方程，然后像我们对原子中的轨道那样，用电子对填充它们。在实践中，我们实际上只对源于组成原子价轨道的 MO 感兴趣，因为这些是参与键合的轨道。我们特别感兴趣的是前沿轨道，即最高占据分子轨道（HOMO）和最低未占分子轨道（LUMO）。能量低得多的填充轨道（即核心轨道）不参与键合，能量更高的空轨道也不参与键合。然而，这些轨道在光化学和光谱学中很重要，光化学和光谱学涉及从占据轨道到空轨道的电子跃迁。如图 2.1.2 所示，使细胞染色的荧光染料通过将 HOMO 中的电子提升到空 MO 来吸收光，并在电子降回原始能级时发出光。

作为 LCAO-MO 方法的一个例子，我们可以从两个 AO φ₁ 和 φ₂（图 2.1.1）构建 HCl 分子的两个 MO（ψ₁ 和 ψ₂）。为了进行这两种线性组合，我们写道

$\psi _{1}=c_{1}\phi _{1}+c_{2}\phi _{2}$

以及

$\psi _{2}=c_{1}\phi _{1}-c_{2}\phi _{2}$

当构成它们的两个原子轨道 (AO) 相同时，系数 c₁ 和 c₂ 将相等（或几乎相等），例如，当两个氢 1s 轨道组合形成 H₂ 中的成键和反键分子轨道 (MO) 时。当 AO 之间存在能量差时，它们将不相等，例如当氢 1s 轨道和氯 3p 轨道组合形成极性 H-Cl 键时。

节点

波函数 φ 和 ψ 是振幅，与在空间某一点找到电子的概率有关。它们有带 (+) 或 (-) 符号的瓣，我们用阴影或颜色来表示。在波函数改变符号的地方，我们有一个节点。正如您在图 2.1.1 中看到的，MO 中的节点是由于 (+) 和 (-) 波函数的相消干涉造成的。通常，节点越多，轨道的能量越高。

在上面的例子中，我们画出了 Cl 3p_z 轨道的简化图以及由此产生的 MO，省略了径向节点。回想一下，2p 轨道没有径向节点，3p 轨道有一个，如图 2.1.3 所示。4p 轨道有两个径向节点，依此类推。我们通过组合 AO 制成的 MO 也具有这些节点。

图 2.1.3。2p 和 3p 轨道的节点结构

归一化：我们将波函数平方以获得概率，概率总是正数或零。因此，如果一个电子在轨道 φ₁ 中，找到它在点 xyz 的概率是 φ₁(x,y,z) 的平方^[1]。当我们组合 AO 制成 MO 时，总概率不会改变，因此对于组合 φ₁ 和 φ₂ 制成 ψ₁ 和 ψ₂ 的简单情况，

$\psi _{1}^{2}+\psi _{2}^{2}=\phi _{1}^{2}+\phi _{2}^{2}$

图 2.1.4。原子轨道的波函数随距离呈指数衰减。当两个原子靠得很近时，轨道重叠不为零，如上图中 1s 轨道的示意图所示。下图显示了距离太远而无法相互作用的轨道。在这种情况下，S 和 β 都接近零。

重叠积分

两个原子轨道 φ₁ 和 φ₂ 之间的空间重叠由重叠积分 S 描述，

$S_{12}=\int \phi _{1}^{*}\phi _{2}\,\mathrm {d} \tau$

其中积分是在整个空间上 ($\mathrm {d} \tau =\mathrm {d} x\,\mathrm {d} y\,\mathrm {d} z$).

成键和反键 MO 的能量

成键和反键轨道的能量强烈依赖于原子之间的距离。图 2.1.5 针对氢分子 H₂ 说明了这一点。在很长的距离上，H 1s 轨道的同相和异相组合之间基本上没有能量差异。随着它们越来越靠近，同相（成键）组合的能量下降，因为电子在两个带正电的原子核之间共享。能量在平衡键长 (0.74 Å) 处达到最小值，然后随着原子核越来越靠近，能量再次上升。反键组合在原子核之间有一个节点，因此它的能量随着原子核的靠近而不断上升。

图 2.1.5。H₂ 分子成键和反键轨道的能量随距离的变化

在平衡键长处，成键和反键分子轨道的能量 (ψ₁, ψ₂) 分别低于和高于原子基轨道的能量 φ₁ 和 φ₂。图 2.1.6 显示了 H₂ 分子的 MO 的情况。

图 2.1.6。H₂ 分子的分子轨道能级图

一个电子在原子轨道中的能量是 α，即库仑积分。

$\alpha =\int \phi _{1}^{*}H\phi _{1}\,\mathrm {d} \tau =\int \phi _{2}^{*}H\phi _{2}\,\mathrm {d} \tau$

其中 H 是哈密顿算符。本质上，α 代表原子轨道 φ₁ 或 φ₂ 中电子的电离能。

AO 和 MO 之间的能量差由交换积分 β 决定，

$\beta =\int \phi _{1}^{*}H\phi _{2}\,\mathrm {d} \tau$

β 是一个重要的量，因为它告诉我们分子键能的信息，以及成键和反键轨道之间的能量差。对于多电子分子，计算 β 并不容易，因为我们无法解析地求解薛定谔方程以获得波函数。但是，我们可以进行一些近似来数值计算能量和波函数。在休克尔近似中，它可用于获得有机分子中 π 分子轨道的近似解，我们通过令 S=0 并对任何彼此不相邻的 p 轨道令 H=0 来简化数学。扩展休克尔方法^[2]，由罗尔德·霍夫曼开发，以及其他半经验方法可用于快速获得各种分子和扩展固体的相对轨道能量、近似波函数和分子轨道简并性。现在在软件包中可以轻松获得更复杂的从头算方法，可用于计算分子和固体的精确轨道能量。

我们可以通过应用归一化条件得到氢分子的系数 c₁ 和 c₂

$\psi _{1}={\frac {1}{\sqrt {2}}}{\frac {\phi _{1}+\phi _{2}}{1+S}}\qquad {\text{(bonding orbital)}}$

以及

$\psi _{1}={\frac {1}{\sqrt {2}}}{\frac {\phi _{1}-\phi _{2}}{1-S}}\qquad {\text{(antibonding orbital)}}$

当 S≈0 时，我们可以消除 1-S 项，两个系数都变为 1/√2

请注意，H₂ 的 MO 图中的成键轨道被稳定了 β/(1+S) 的能量，而反键轨道被不稳定了 β/(1-S) 的能量。也就是说，反键轨道在能量上比成键轨道下降更多。这意味着 H₂ (ψ₁²ψ₂⁰) 在能量上比两个 H 原子更稳定，但 He₂ 具有四个电子 (ψ₁²ψ₂²) 相对于两个 He 原子来说是不稳定的。

键级：在任何 MO 图中，键级可以计算为 ½ (成键电子数 - 反键电子数)。对于 H₂，键级为 1，对于 He₂，键级为零。

键强度和键长：当我们使用 MO 理论计算键时，我们使用上面的公式来计算净键级。这个公式意味着 H₂⁺ 和 H₂^- 分子都具有 1/2 的键级，因为有一个净成键电子。然而，在实验中，我们发现 H₂^- 中的键比 H₂⁺ 中的键长得多，也弱得多。下表总结了仅使用它们的 1s 原子轨道形成 σ 和 σ* 分子轨道的分子和离子的键强度和键长。

双原子分子和离子的 MO 配置、键长和键强度

分子	电子数	MO 配置	净成键电子数	键级	键长 (Å)	键能 (kJ/mol)
H2+	1	σ1s1	1	1/2	1.07	256
H2	2	σ1s2	2	1	0.74	436
H2-	3	σ1s2σ*1s1	1	1/2	-	156
He2+	3	σ1s2σ*1s1	1	1/2	1.08	230
He2	4	σ1s2σ*1s2	0	0	-	-

H₂⁺ 和 H₂^- 中键强度之间显著差异的出现是由于三电子 H₂^- 离子中存在电子-电子排斥，而在 H₂⁺ 中不存在电子-电子排斥。我们还观察到，三电子 He₂⁺ 离子的键比 H₂^- 中的键强得多。在 He₂⁺ 的情况下，电子与 He²⁺ 核的正电荷之间的吸引力抵消了电子-电子排斥。故事的寓意是，我们绘制的 MO 图（就像我们从薛定谔方程绘制的原子轨道一样）是针对单电子原子计算的，但在真实的（多电子）原子和分子中，我们在估计或计算键能时必须考虑电子-电子排斥。

异核情况（例如，HCl） - 极性键

这里我们引入了构成化学键的两个原子之间的电负性差异。H 1s 轨道中电子的能量高于 Cl 3p_z 轨道中电子的能量（更容易电离）。这导致形成的分子轨道 ψ₁ 和 ψ₂ 之间的能量差更大，如图 2.1.7 所示。原子轨道之间电负性差异越大（Δα 越大），成键轨道就越具有“φ₂ 特征”，即在这种情况下的 Cl 3p_z 轨道越相似。这与 H-Cl 具有极性单键的想法一致：两个电子驻留在主要定位在 Cl 原子上的成键分子轨道中。

图 2.1.7. HCl 分子的分子轨道能级图

反键轨道（空）具有更多的 H 特征。键级仍然为 1，因为成键轨道中有两个电子，而反键轨道中没有电子。

极端情况 - 离子键 (NaF)：非常大的 Δα

在这种情况下，AO 之间没有太多混合，因为它们的能量相差很远（图 2.1.8）。两个成键电子都位于 F 原子上，因此我们可以将分子写成 Na⁺F^-。请注意，如果我们使用光将电子从 ψ₁ 激发到 ψ₂，则得到的电子构型将是 (ψ₁¹ψ₂¹)，我们将有 Na⁰F⁰。这被称为电荷转移跃迁。

图 2.1.8. 说明 NaF 分子中离子键的分子轨道能级图

到目前为止，分子轨道理论的总结

• 加减 AO 波函数以构成 MO。两个 AO → 两个 MO。更一般地说，MO 的总数等于 AO 基组轨道的数目。

• 我们展示了最简单的情况（只有两个基组轨道）。更精确的计算使用更大的基组（更多 AO），并使用哈密顿算符 H 的势能函数的数学友好近似值来求解给出最低总能量的 c 矩阵。

• 更多节点 → 更高能量 MO

• 键级 = ½ (成键电子数 - 反键电子数)

• 键极性 在 MO 图像中表现为轨道“特征”。

• 能量相差很远 的 AO 在结合形成 MO 时不会发生太多相互作用。

  2.2 轨道对称性

图 2.2.1. σ 对称性的示例。

当涉及到许多价 AO 时，分子的 MO 图像会变得复杂。我们可以通过注意到（这里没有证明）不同对称性的轨道（相对于分子）不会相互作用，从而极大地简化问题。分子的对称操作（可以包括旋转、镜面、反转中心等），以及分子中键和轨道的对称性类别，可以根据群论进行严格定义。在这里，我们将采用一种简单的方法来解决这个问题，该方法基于我们对三维物体的对称性的直观理解，如图 2.2.1 所示。

AO 必须具有相同的节点对称性（由分子对称操作定义），否则它们的重叠为零。

例如，在 HCl 分子中，有一个独特的对称轴 →，它通常定义为笛卡尔 z 轴，如图 2.2.2 所示。

图 2.2.2. 具有 σ 和 π 对称性的轨道不会相互作用。

从该图中我们可以看出，H 1s 轨道在绕键轴旋转 180° 时保持不变。然而，相同的旋转会反转 Cl 3p_y 波函数的符号。因为这两个轨道具有不同的对称性，所以 Cl 3p_y 轨道是非键的，并且不会与 H 1s 相互作用。Cl 3p_x 轨道也是如此。p_x 和 p_y 轨道具有 π 对称性（包含键轴的节点平面），在 MO 能级图中标记为 π_nb，如图 2.2.3 所示。相反，H 1s 和 Cl 3p_z 轨道都具有 σ 对称性，这也是图 2.2.1 中所示的陶罐的对称性。因为这些轨道具有相同的对称性（在分子的点群中），所以它们可以形成图 2.1.1 中所示的成键和反键组合。

包括 Cl 原子所有价轨道的 HCl 的 MO 图示于图 2.2.3 中。两个 Cl 价轨道 (3p_x 和 3p_y) 具有错误的对称性，无法与 H 1s 轨道相互作用。Cl 3s 轨道与 H 1s 具有相同的 (σ) 对称性，但它的能量低得多，因此几乎没有轨道相互作用。因此，Cl 3s 轨道的能量仅受分子形成的轻微影响。因此，π_nb 和 σ_nb 轨道中的电子对是非键的。

图 2.2.3. HCl 分子的能级图，显示了来自价 AO 的 MO。

请注意，图 2.2.3 中的 MO 结果（1 个键和 3 对非键电子）与我们从 HCl 的价键理论中得到的相同。非键轨道定位在 Cl 原子上，正如我们从价键图像中推断的那样。

为了区分它与 σ 成键轨道，在这种情况下为空的 σ 反键轨道用星号表示。

  2.3 σ, π 和 δ 轨道

图 2.3.1. 八氯二铼(III) 阴离子，[Re₂Cl₈]²⁻，它具有四重 Re-Re 键。

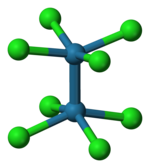
无机化合物使用 s、p 和 d 轨道（以及更少见的 f 轨道）来构成成键和反键组合。这些组合导致σ, π, 和 δ 键（以及反键）。

您已经熟悉了有机化合物中的 σ 和 π 键。在无机化学中，π 键可以由 p 和/或 d 轨道形成。δ 键比较少见，是由 d 轨道的面对面重叠形成的，例如在 Re₂Cl₈^2- 离子中。Cl 原子在该阴离子中重叠的事实是 δ 键存在的证据。

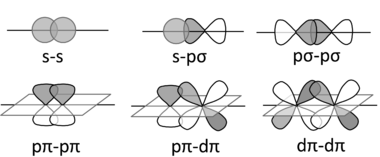
下面绘制了一些 s、p 和 d 轨道的 σ（顶行）、π（底行）和 δ 键合组合（右）。在每种情况下，我们都可以根据 AO 波函数的符号形成成键或反键组合。由于 pπ-pπ 键合涉及 p 轨道的侧向重叠，因此它在第二周期元素（C、N、O）中最为常见。较重元素的 π 键化合物很少见，因为原子核较大，无法形成良好的 π 重叠。出于这个原因，含有 C=C 双键的化合物非常常见，而含有 Si=Si 键的化合物则很少见。δ 键 通常比 σ 和 π 键弱得多。含有金属-金属 δ 键的化合物出现在过渡系列的中间。

    

过渡金属 d 轨道也可以形成 σ 键，通常与配体上具有适当对称性的 s-p 杂化轨道形成。例如，膦（R₃P:）是与过渡金属形成配合物的良好 σ 供体，如右图所示。

pπ-dπ 键合在过渡金属配合物中也很重要。在金属羰基配合物（如 Ni(CO)₄ 和 Mo(CO)₆）中，填充的金属 d 轨道与 CO 分子的空 π 反键轨道（LUMO）之间存在侧向重叠，如左侧的图所示。这种相互作用增强了金属-碳键，但削弱了碳-氧键。C-O 红外拉伸频率是键强度诊断指标，可用于估算从金属 d 轨道转移到 CO π 反键轨道的电子数。

与膦配合物同样存在这种反键合，膦配合物具有空 π 轨道，如右图所示。含有卤素配体的过渡金属配合物也可能具有明显的 pπ-dπ 键合，其中配体上的填充的 pπ 轨道将电子密度捐赠给未填充的金属 dπ 轨道。我们将在第 5 章中遇到这些键合情况。

  2.4 双原子分子

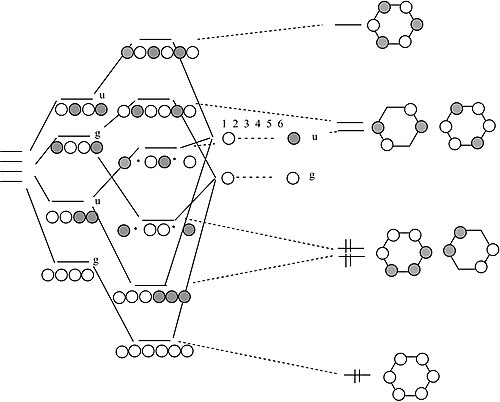
价键理论对于一些第二周期双原子分子来说是失效的，最著名的例子是 O₂，它预测了一个反磁性的、双键的分子，具有四个孤对电子。O₂ 确实具有双键，但它在地面态具有两个未配对电子，这种性质可以用 MO 图来解释。我们可以为这些分子构建 MO 能级图，如下所示

                               Li₂, Be₂, B₂, C₂, N₂                                                         O₂, F₂, Ne₂

当 2s 和 2p AO 在能量上很好地分离时，我们得到了右侧的更简单的双原子 MO 图，如 O₂、F₂ 和 Ne₂。左侧的图是由 σ_2s 和 σ_2p MO 的混合产生的，这些 MO 在 Li₂、Be₂、B₂、C₂ 和 N₂ 中能量接近。这种混合的作用是将 σ_2s* 的能量降低，将 σ_2p 的能量提高，以至于 pπ 轨道位于 σ_2p 轨道下方。请注意，π 和 π* 轨道的能量不受 s-p 混合的影响，因为对称性考虑因素。π 和 π* 轨道具有“u”对称性，这意味着它们关于反转操作是反对称的。σ 和 σ* 轨道具有“g”对称性，这意味着它们在反转后保持不变（见第 2.5 节）。异核双原子分子和离子（如 CO、NO 和 NO⁺）也由于 s-p 混合而具有左侧所示的能级顺序。

如果您想看看这些成键和反键分子轨道的样子，可以在利物浦大学结构和键合网站上找到一个关于 CO 分子中的 MO 的良好动画。

为什么 O₂ 和 F₂ 不发生 sp 轨道混合？原因与轨道的能量有关，这些能量在左侧的简单图像中没有按比例绘制。当我们从 Li 到 F 横跨周期表的第二周期时，我们逐渐向原子核添加质子。2s 轨道在原子核处具有有限的幅度，因此它比 2p 轨道更“感受到”增加的核电荷。这意味着，当我们横跨周期表（以及稍后我们将看到，当我们向下移动周期表时），s 轨道和 p 轨道之间的能量差变得很大，超过了键能。随着 2s 和 2p 能量在能量上越来越远离，轨道之间的相互作用（即混合）越来越少。

右侧显示了轨道能量图。由于 1s 和 2s/2p 轨道之间的能量差非常大，因此我们将它们绘制在不同的能量尺度上，其中 1s 在左侧，2s/2p 在右侧。对于第二周期左侧的元素（Li、Be、B），2s 和 2p 能量仅相差几 eV。对于 O 和 F，能量差变得非常大——超过 20 电子伏特（1930 kJ/mol）。由于单键能通常约为 3-4 eV，因此这种能量差在我们的 MO 图的尺度上将非常大。对于周期表第二周期的所有元素，1s（核心）轨道的能量比 2s/2p（价电子）轨道低得多，因此在绘制我们的 MO 图时不需要考虑它们。

  2.5 轨道填充

根据泡利不相容原理和洪特规则，MO 从底部开始填充，就像我们对原子轨道所做的那样。

问题：洪特规则的量子力学基础是什么？

考虑两个简并轨道的例子，例如第二周期双原子分子中的 π 或 π* 轨道。如果这些轨道每个都包含一个电子，它们的自旋可以平行（洪特规则优先）或反平行。泡利不相容原理指出，一个轨道中不能有两个电子具有相同的量子数集（n、l、m_l、m_s）。这意味着，在平行情况下，泡利不相容原理阻止电子访问对方的轨道。在反平行情况下，它们可以自由地来去，因为它们具有不同的 m_s 量子数。然而，在同一个轨道中有两个电子在能量上是不利的，因为同种电荷相互排斥。因此，平行排列，由于泡利不相容原理，具有更低的能量。

对于 O₂（12 个价电子），我们得到了下面的 MO 能级图。右侧显示了分子轨道的形状。

氧分子轨道图

红巨星的特点是它们大气中存在 C₂ 分子。由于 C₂ 的净键级为 2，因此它在从气相冷却到形成其他形式的碳（如富勒烯、石墨和金刚石）时会迅速反应，所有这些形式对于每两个碳原子来说都有四个键。

这种 MO 的能量排序正确地预测了π* 轨道中存在两个未配对电子，以及净键级为 2（8 个成键电子和 4 个反键电子）。这与氧分子实验观察到的顺磁性一致。

MO 理论对第二周期双原子分子的其他有趣预测是，C₂ 分子的键级为 2，而 B₂ 分子具有两个未配对电子（均已通过实验验证）。

我们还可以预测（使用上面的 O₂、F₂、Ne₂ 图），NO 的键级为 2.5，CO 的键级为 3。

轨道标记中的“g”和“u”符号，我们只在中心对称分子中使用，指的是它们关于反转的对称性。 gerade（g）轨道是对称的，这意味着通过中心反转不会改变轨道。 ungerade（u）表示轨道的符号在反转操作中反转。由于 g 和 u 轨道具有不同的对称性，因此它们之间的重叠为零。正如我们将在下文中看到的那样，根据 g 和 u 对称性对轨道进行分解简化了在更复杂的分子（如丁二烯和苯）中构建分子轨道的任务。

上面显示的轨道形状是使用分子的单电子模型计算得到的，就像我们对类氢原子轨道（AO）进行计算以获得 s、p 和 d 轨道的形状一样。为了获得多电子分子（即所有真实分子）的准确的分子轨道（MO）能量和图，我们必须考虑电子是“关联”的，也就是说，由于电子的负电荷，它们在分子中会互相避开。这个问题无法用解析方法求解，只能通过使用密度泛函理论（DFT）在数值计算中近似求解。我们将在第 10 章学习电子关联在固体（例如超导体）中的影响。

  2.6 π 键的周期性趋势

正如我们在第 2.3 节中提到的，pπ 键几乎总是涉及第二周期元素。

我们在第二周期双原子分子（B₂…O₂）的 MO 图中遇到由 p 轨道侧面重叠形成的 π 键。重要的是要记住，π 键比由相同 AO 形成的 σ 键弱，如果涉及第二周期以外的元素，则 π 键特别弱。

示例

乙烯和亚硅烷结构的比较

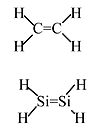
乙烯：稳定的分子，在没有催化剂的情况下不会聚合。

亚硅烷：从未被分离出来，会自发聚合。计算表明，气相中相对于单键（三重态）H₂Si-SiH₂ 的稳定性为 117 kJ/mol。

白磷 (P₄) 是一种软的蜡状固体，在空气中会自燃，燃烧时发出明亮的火焰并产生大量的白色 P₄O₁₀ 烟雾。此处显示的样品是在水中拍摄的，以防止氧化反应。

Si 原子的巨大氖核抑制了 3p 轨道的侧面重叠→ π 键很弱。

其他示例：P₄ 与 N₂

元素磷和氮结构的比较

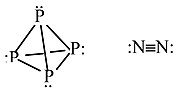
P 不能与自身形成 π 键，因此它形成具有显著环张力的四面体分子。这种 P 的同素异形体在空气中会自燃。固态白磷会非常缓慢地转化为红磷，这是一种更稳定的同素异形体，包含金字塔形 P 原子的片层，每个 P 原子与三个相邻原子键合，并带有一个孤对电子。

N 可以形成 π 键，因此 N₂ 具有非常强的三键，是一种相对惰性的双原子气体。

硅聚合物 (R₂SiO)_n 用于不粘炊具（如这些纸杯蛋糕模具）、橡皮泥、软体机器人 和许多其他应用。

(CH₃)₂SiO 与 (CH₃)₂CO

聚硅氧烷和丙酮结构的比较

“RTV” 硅聚合物（Si 与 4 个单键键合）与丙酮（C=O 双键）。硅树脂是柔软的、灵活的聚合物，可以在不分解的情况下加热到高温（>300 °C）。丙酮是一种易燃的分子液体，沸点为 56 °C。


另外比较
SiO₂ (mp ~1600°C) 与 CO₂ (在 -78°C 升华)

S₈ (固体，环状结构) 与 O₂ (气体，双键)

例外

第二周期元素可以与第三周期元素中最小的 P、S 和 Cl 形成相当强的 π 键。因此，我们在含硫氮化合物（如 S₂N₂ 和 S₃N₃^-）中发现 S=N 键，在磷酸和 P₄O₁₀（左侧显示）中发现 P=O 键，在 SO₂（与臭氧类似）中发现离域的 π 分子轨道。

  2.7 三中心键

我们使用 MO 理论解决的许多（但不是所有）问题都源于 H₂ 分子的 MO 图（图 2.1.5），这是一个双中心键的情况。其他的问题我们将通过类比于 H₃⁺ 离子来解决，这引入了三中心键的概念。

我们可以用直线形或三角形几何形状来绘制 H₃⁺ 离子（以及 H₃ 和 H₃^-）。

H₃⁺ 的沃尔什相关图

H₃⁺ 的沃尔什图

关于此图的一些重要要点

• 对于离子的直线形，最高和最低 MO 相对于分子中的反转中心是对称的。请注意，中心的 1s 轨道具有g 对称性，因此根据对称性，它与两端两个 1s 轨道的u 组合没有重叠。这使得 σ_u 轨道成为非键合轨道。

• 在分子的三角形形状中，源自 σ_u 和 σ*_g 的轨道变得简并（即，根据对称性，它们具有完全相同的能量）。术语符号“e”表示双重简并。我们将在后面看到，“t”表示三重简并。请注意，我们放弃了三角形轨道的“g”和“u”，因为三角形没有反转中心。

• 三角形形状最稳定，因为 H₃⁺ 中的两个电子在最低轨道中具有较低的能量。弯曲分子会在两端的 1s 轨道之间产生第三个键合相互作用。

XH₂ (X = Be, B, C…) 的 MO 图

这比 H₃ 更复杂，因为 X 原子既有 s 轨道又有 p 轨道。但是，我们可以对轨道进行对称性分解，并通过类比于 H₂ 分子来解决问题。

XH₂ 的 MO 图

关于此 MO 图的一些关键点

• 在具有反转对称性的分子的直线形中，X 原子的 2s 和 2p 轨道分解成三个对称性类别

2s = σ_g

2p_z = σ_u

2p_x, 2p_y = π_u

• 类似地，我们可以看到，两个 H 1s 轨道形成了两个线性组合，一个具有 σ_g 对称性，另一个具有 σ_u 对称性。它们看起来像H₂ 分子的键合和反键合 MO（这就是我们说我们用这个问题来解决这个问题的原因）。

• π_u 轨道必须是非键合的，因为没有 H 1s 轨道的组合具有 π_u 对称性。

• 在 MO 图中，我们制作了 σ_g 和 σ_u 的键合和反键合组合。对于 BeH₂，我们然后用四个价电子填充最低的两个轨道，并发现（不出所料）分子具有两个键，可以写成H-Be-H。相关图表明，分子的弯曲形状应该不太稳定。

关于此 MO 图的一个有趣的论点是，很难事先预测 CH₂ 应该是直线形还是弯曲形。1970 年，查尔斯·本德和亨利·谢弗使用量子化学计算预测，基态应该是一个弯曲的三重态，H-C-H 角为 135°。 当时最好的实验表明亚甲基是一个线性单线态，理论学家认为实验结果是错误的。后来的实验证明他们是正确的！

“理论是没有人相信的东西，除了提出它的人。实验是每个人都相信的东西，除了做它的人。”——爱因斯坦

  2.8 构建更复杂分子的 MO：NH₃、P₄

NH₃ 的 MO 图

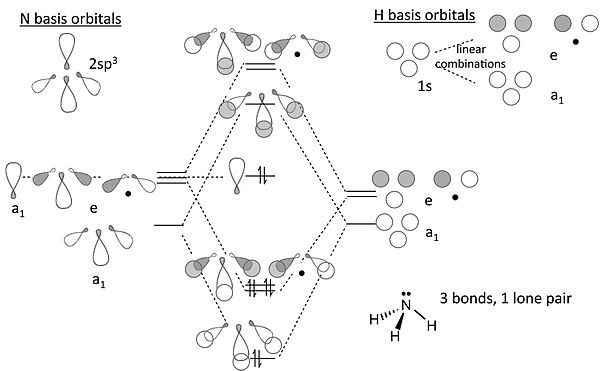
我们现在可以尝试构建 NH₃ 的 MO 图，以此为基础，我们获得了三角形 H₃⁺ 的结果。

氨分子的分子轨道图

关于氨的 MO 图的说明

• 从端面观察，p 轨道或 sp_x 杂化轨道看起来就像 s 轨道。因此，我们可以使用我们在 s 轨道中（对于 H₃⁺）开发的解来建立氮 sp³ 轨道与 H 1s 轨道的 σ 键合和反键合组合。

• 我们现在构建氮原子的 sp³ 杂化轨道，并将它们定向，使得一个向上，另外三个形成四面体的三角形底座。后面三个，通过与 H₃⁺ 离子的类比，转化为一个完全对称轨道（“a₁”）和一个 e 对称性对。位于四面体顶部的杂化轨道也具有 a₁ 对称性。

• 三个氢 1s 轨道也形成了一个 a₁ 组合和一个（双重简并）e 组合。我们使用相同对称性的氮轨道构建键合和反键合组合。N 上剩余的 a₁ 轨道是非键合的。虚线显示了 a₁ 和 e 对称性的基轨道与分子轨道之间的关联。

• 在 8 电子 NH₃ 分子中，结果是三个 N-H 键和一个孤对电子位于 N 上，这与价键理论相同（但工作量要多得多！）。

P₄ 分子和 P₄²⁺ 离子

通过与 NH₃ 的类比，我们可以构建 P₄ 四面体的一个顶点的 MO 图，然后将结果乘以 4 来获得整个分子的成键图。一个重要的区别是 P₄ 中 s-p 杂化相对较少，因此孤对电子轨道具有更多的 s 特征，能量低于主要由 pσ 构成的成键轨道。

P₄: 20 个价电子

P4 分子的分子轨道图

移走 2 个电子形成 P₄²⁺

最高占据分子轨道是成键轨道 → 断开一条键，剩下 5 条键

方形形式减轻环张力，(60° → 90°)

P42+ 离子的结构

2 个 π 电子

芳香性 (4n + 2 规则)

  2.9 MO 图中 σ 和 π 轨道的同源性

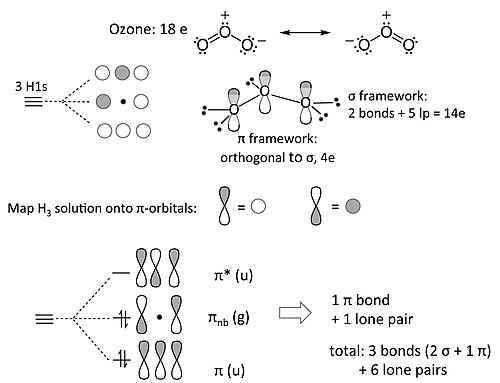
臭氧分子（以及包含三个非 H 原子的类似 18e 分子，例如 NO₂^- 和烯丙基阴离子 [CH₂-CH-CH₂]^-）是三中心四电子 π 成键的例子。我们对臭氧的 MO 处理完全类似于 4 电子 H₃^- 阴离子。我们将该解决方案映射到此解决方案上，如下所示

通过类比 H3- 构建臭氧的 π 系统

罗阿尔德·霍夫曼教授关于轨道对称性的观点帮助解释了有机和有机金属分子的成键和反应性，以及扩展固体的结构和性质。

非键合 π 轨道在中心 O 原子上有一个节点。这意味着 π 系统中的非键合电子对被两个末端 O 原子共享，也就是说，形式电荷被这些原子共享。这与臭氧的八隅体共振结构一致。

将一组 s 轨道的解映射到 π 成键问题，这是一个简单示例，它体现了一个更广泛的原理，称为等电子原理。这个想法由康奈尔大学的罗阿尔德·霍夫曼广泛发展，已被用于理解有机金属化合物中的成键和反应性。 <sup>在等电子原理中，对称性原理（如上面 H₃- 和臭氧之间的类比所示）被用于从更简单的分子片段构建包含 d 边界轨道的复杂分子的 MO 图。


三碘离子。 I₃- 是 3 中心 4 电子成键的类似（但似乎更复杂）的例子。每个 I 原子具有 4 个价轨道 (5s, 5p_x, 5p_y, 5p_z)，总共 12 个边界轨道，而 I₃- 阴离子具有 22 个电子。

我们可以通过回忆两个周期性趋势来简化问题</sup>

• 在周期表的第二周期之后，s-p 轨道分裂较大，相对于键能而言。因此，5s 轨道能量较低，并且收缩得过于紧密，无法与其邻居形成键。
• 5p 轨道的 π 重叠非常弱，因此 5p_x 和 5p_y 轨道也将是非键合的。
  

这仅留下三个 5p_z 轨道来形成成键/非键合/反键组合。同样，这个问题与臭氧或 H₃^- 完全类似。

从边界 5pz 轨道构建 I3- MO 图

计算轨道，我们从非键合 5s、5p_x 和 5p_y 轨道获得 9 个孤对电子，以及从上面的 5p_z 轨道组合获得 1 个键和 1 个孤对电子。总共 10 个非键合对和 1 个键解释了离子中的 22 个电子。非键合 5p_z 对局域在末端 I 原子上，使每个原子的形式电荷为 -1/2。这个 MO 描述与我们在第 1 章中开发的 I₃^- 的八隅体无键共振图像完全一致。

  2.10 π 共轭体系的链和环

乙烯分子

        乙烯：π 系统类似于 H₂ 中的 σ 成键

H2 和乙烯轨道的同源性

从顶部或底部观察，乙烯 π 轨道看起来像 H₂ σ 轨道。因此，我们可以将 H 原子链和环的解映射到 π 轨道链和环上（就像我们对 O₃ 的三轨道情况所做的那样）。

四個 H 原子或 π 轨道的链和环（H₄ 或丁二烯）

H4 或丁二烯的 MO 图

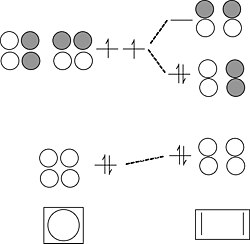
关于这个 MO 图的一些说明

• 在线性形式的分子中，AO 的组合形成一个阶梯，具有均匀间隔的能级，交替排列为 g – u – g – u …。每个后续轨道都多一个节点。对于具有偶数个原子的 σ 或 π 轨道的线性链，这是一个通用的规则。

• 在分子的环状形式中，底部有一个非简并轨道，顶部有一个非简并轨道，中间有一个简并轨道阶梯。对于具有偶数个原子的环状分子，这也是一个通用的规则。这就是芳香族化合物4n+2 规则的起源。

• H₄ 有四个价电子，类比地，丁二烯有四个 π 电子。这些电子填充了分子线性形式的最低两个 MO，对应于丁二烯中的两个共轭 π 键 (H₂C=CH-CH=CH₂)。

• 在分子的环状形式中，简并轨道是单占据的。分子可以通过扭曲成一个褶皱的矩形来打破简并性（并降低能量）。对于反芳香族环状分子（4n 规则），这是一个通用的规则。因此，环丁二烯应该是反芳香族，并且应该具有两个单键和两个双键，它们没有被共振离域。

环丁二烯的反芳香性

环丁二烯实际上是一个非常不稳定的分子，因为它会聚合以减轻环张力。该分子的空间位阻衍生物确实具有 MO 理论预测的褶皱矩形结构。

苯 π 轨道

我们如何从 4 原子链过渡到 6 原子链？

通过类比我们从 2 原子链过渡到 4 原子链的过程，我们现在从 4 过渡到 6。我们从 4 原子链的轨道开始，这些轨道形成一个 g 和 u 轨道的阶梯。然后我们对我们正在添加在两端的两个原子进行 g 和 u 组合。通过将 g 与 g 相结合，将 u 与 u 相结合，我们最终得到 6 个原子的字符串的解。将这些轨道闭合成一个循环，我们就得到了苯分子的 π 分子轨道。结果是三个 π 键，正如我们预期的那样。苯符合 4n+2 规则 (n=2)，因此是芳香族化合物。

构建苯的 pi MO

在这里，我们使用等电子原理从 s 轨道的组合构建了 π 键合体系的 MO 图，例如乙烯和苯。它提出了一个有趣的问题，即芳香族 4n+2 规则是否可能适用于 s 轨道体系，即，如果三个 H₂ 分子可以结合在一起形成一个芳香族 H₆ 分子。事实上，最近在金刚石砧座中对超高压下氢的研究表明，这样的结构确实会形成。存在一个固态氢相，其中包含扭曲的六元环片，类似于在石墨或石墨烯中发现的完全连接的二维六元环网络。 <sup>具有四个成员环中六个 π 电子的阴离子也是芳香族化合物。例如，环丁烷的二阴离子 C₄H₄2-，以及 15 族阴离子 Bi₄2-、Sb₄2-、As₄2- 和 P₄2-。

现在应该从我们对四轨道和六轨道分子的 MO 图的构建中很明显，我们可以继续添加原子轨道来形成 8、10、12... 原子的链和环。在每种情况下，g 和 u 轨道形成一个 MO 阶梯。在 N 原子链阶梯的底部，MO 中没有节点，并且我们为每个阶梯添加一个节点，直到我们到达顶部，在那里有 N-1 个节点。另一种说法是，从底部算起的轨道 x 中电子的波长（1,2,3...x,...N）是 2Na/x，其中 a 是原子之间的距离。我们将在第 6 章和第 10 章中发现，我们可以从这个模型中了解很多关于金属和半导体的电子性质，使用无限原子链作为晶体的模型。</sup>

  2.11 讨论问题

二茂铁

• 推导出线性 H₂O 和弯曲 H₂O 的分子轨道图。
• 解释为什么 H₂O 和 H₂S 的键角不同。
• 我们已经推导了四碳和六碳链和环的π体系的MO图。重复此练习，针对五碳链和五碳环（例如，环戊二烯负离子），从H₂和H₃的MO图像开始。这个棘手的难题帮助我们理解了二茂铁的电子结构，并获得了1973年的诺贝尔奖。

  2.12 习题

1. 氢原子的电离能为 1312 kJ/mol，H₂⁺分子离子的键解离能为 256 kJ/mol。H₂⁺分子离子的重叠积分S由表达式S = (1 + R/a₀ + R²/3a₀²)exp(-R/a₀)给出，其中R为键长（1.06 Å），a₀为玻尔半径，0.529 Å。H₂⁺的α和β（单位为 kJ/mol）的值是多少？

2. 使用H₂的分子轨道能级图比较H₂⁺和H₂^-的键序。H₂^-离子的键解离能为 156 kJ/mol，而H₂⁺的键解离能为 256 kJ/mol。这是你根据键序预期的吗？为什么H₂^-的键解离能比H₂⁺的键解离能低得多？

3. HHe的键序是多少？为什么这种化合物从未被分离出来？

4. 你预计Be₂⁺分子离子在气相中会稳定吗？总键序是多少，有几个净σ键和π键？

5. 对气相6族二氟化物（XF₂）分子中F-X-F键角的以下周期性趋势给出合理的解释。（提示 - 它与s和p轨道能量的趋势有关；见第1章，第1.2节）

化合物	F-M-F角度（度）
OF2	103
SF2	99
SeF2	97
TeF2	95

6. 氧的最稳定同素异形体是O₂，但类似的硫分子（S₂）相对于S₈同素异形体不稳定。解释原因。

7. 使用分子轨道理论，说明为什么H₃分子具有三角形（或弯曲）而不是线性形状。

8. 使用MO理论确定以下分子的键序和未成对电子的数量：（a）O₂^-，（b）O₂⁺，（c）NO⁺，和（d）NO^-。使用鲍林公式和中性NO分子中的键长（1.151 Å）估计NO^-和NO⁺中的键长。

10. 比较MO理论和价键理论在描述以下分子的成键方面的结果：（a）CN^-和（b）中性CN。根据MO理论，在第二周期双原子分子中，键序可能大于3吗？

11. 中性BN分子仅在气相中稳定。该分子聚合形成固态氮化硼，它以石墨状和超硬金刚石状形式存在。绘制BN分子的分子轨道能级图。确定σ和π键序以及未成对电子的数量。

12. 气相BN分子的键长为 1.44 Å。使用鲍林公式和你在问题11中确定的键序，计算氨硼烷 (H3B-NH3) 中的 B-N 键序，其中键长为 1.658 Å。你的计算结果与价键理论预期的 B-N 键序一致吗？

13. 绘制线性[FHF]^-离子的MO图。你只需要关注边界轨道，即H 1s 和两个沿成键（z）轴的 F sp_z杂化轨道。HF 键的顺序是什么？原子上的形式电荷是多少？

14. 环辛四烯 (cot) 分子（想象一个有四个双键的停止标志）具有褶皱的环状结构。然而在U(cot)₂中，铀的氧化态为4+，cot配体的形式电荷为2-，8元环是平面的。为什么cot^2-是平面的？

15. 绘制以下原子轨道，包括不同相位的不同阴影、x、y和z轴以及轨道的名称。按能量顺序对它们进行编号，能量最低的轨道为#1，能量增加的轨道为数字增加。不需要剖视图，只绘制表面。3d_x2-y2，2p_x，3d_z2，3s，3p_y，3d_xz，3d_yz。

16. 绘制以下分子轨道，包括不同相位的不同阴影以及轨道的名称。按能量顺序对它们进行编号，能量最低的轨道为#1，能量增加的轨道为数字增加。1σ_2p轨道，2个不同的π*_2p轨道，1σ*_2s轨道，1σ_1s轨道，1σ*_2p 轨道。

17. 绘制一个沃尔什图，展示MO图如何从线性 H-X-H 分子（其中 X 是第二周期元素，如 Be、B、C、N 或 O）转变为弯曲的分子。使用该图预测H₂O分子是线性的还是弯曲的。总键序是否与H₂O的价键图一致？