无机化学导论/化学键概述

分子(和扩展的固体)是由形成化学键的原子构成的。键合理论试图解释为什么分子和固体会形成,它们的结构是什么,为什么有些比其他更稳定,以及它们如何反应。正如我们将在第二章中了解到的,量子力学通过分子轨道 (MO) 理论为我们提供了化学键合最真实的图景。然而,MO 键合描述在概念上很困难,在数学上也很复杂。本章将回顾一些不太严格(但仍然有用)的模型,例如路易斯点结构和价层电子对互斥 (VSEPR) 理论。当与通过轨道杂化和共振概念进行定性量子力学描述结合时,这些简单模型可以帮助我们了解无机分子的结构、稳定性和反应。
化学键理论有着悠久的历史,可以追溯到古希腊原子论者德谟克利特、留基波斯和伊壁鸠鲁学派。他们假设存在着在虚空中运动的不变原子,并将物质的物理性质视为由原子的种类和形状造成的。罗马诗人卢克莱修(约公元前 99 年 - 约公元前 50 年)在他的史诗《论物之本性》中,借鉴了伊壁鸠鲁学派的信仰,以以下方式描述了一些原子和化学键:
在我们看来坚硬而凝结的东西
一定是原子在彼此之间互相勾连,
紧密地结合在一起,就好像
通过树枝状的原子——其中最主要的
是金刚石,蔑视一切打击
坚固的燧石和坚硬的铁
以及黄铜棒,它们在锁中难以移动,
会发出摩擦和尖叫声。但是,液体是什么,形成
流体物质,它们确实必须
由更光滑和圆形的元素组成——因为
它们的球体分别不会粘在一起。
卢克莱修的诗歌读起来很愉快,考虑到当时可用的工具,它对微观世界有一些非凡的见解。然而,现代分析方法表明他的关于钩子和球体的想法是错误的。我们将根据现代化学理论,重新审视卢克莱修提到的物质(金刚石、硅酸盐、铁、黄铜和水)中化学键的性质,以了解为什么它们具有它们所具有的特殊性质。
第一章学习目标
- 能够绘制路易斯点结构,分配形式电荷,预测分子几何形状(包括键角),并计算分子的键级,包括超价分子和离子。
- 使用非键共振描述超价分子。
- 理解并阐明如何通过实验验证分子结构和键合的预测。
- 学习从 s 和 p 原子轨道构建杂化轨道。
- 使用等电子原理设计新的分子和固体。
- 使用键极性参数合理化键强度和化学反应性。
- 相互关联键长和键强度。

原子和分子
原子论,因为它被亚里士多德所摒弃,在科学话语中沉睡了很长时间,直到 17 世纪被伽利略、笛卡尔和伽桑狄重新考虑。道尔顿在 1808 年基于他观察到的氢和氧等元素以特定比例结合(定比定律)假设了现代原子理论,但原子理论在整个 19 世纪的大部分时间里仍然存在争议。汤姆森、卢瑟福、玻尔以及 20 世纪初的其他人在建立了物质确实是包含重核和轻电子的原子组成,以及原子可以存在于可以解释为电子激发到不同能级的激发态时。然而,原子理论并没有为分子中原子的键合态提供一个现成的解释。
1916 年,在现代量子理论充分描述原子轨道的形状之前十多年,路易斯基于经验观察的化合价规则,即原子在分子中的结合比例,提出了八隅律。[1] 事后看来,这个理论可以根据主族元素的观察结果进行合理化,即主族原子可以使用它们的四个价电子轨道(s、px、py 和 pz)来容纳多达八个电子,其中一些或全部电子可能与其他原子共享。在路易斯的模型中,原子的价电子位于立方体的角上,立方体可以共享边或面来完成它们的八隅体。路易斯开发了一种基于点的简写符号来表示这些结构,这些点代表价电子,如图 1.1.1 所示。原子之间共享的一对电子构成一个化学键,也可以用连接原子的线来表示。原子之间共享的四个电子,用两条线表示,是一个双键,依此类推。任何不参与键合的电子对都形成“孤对”,只属于一个原子,因此不参与键合。
路易斯图在简单性方面功能强大。它可以很容易地用来合理化或预测原子的结合比例,对分子的合理和不合理的结构进行排序(包括大型分子),以及合理化许多分子的酸碱性质。重要的是要记住,该模型建立在对原子不稳定的、量子力学前描述的基础上,因此使用它,我们会犯错误。然而,看看我们可以用路易斯模型走多远还是很有用的。
构建分子的八隅体价键图
我们可以使用N-V 方法为任何分子构建一个八隅体图:
- 围绕所有原子形成独立八隅体所需的电子数 = N
- (N = 8 对于非 H 原子,N = 2 对于 H)
- 价电子数 = V(使用族号加起来;不要忘记在离子上的电荷中加或减)
- 共享电子数 = S = N-V;因此键数 = S/2
- 在其他所有地方填入孤对以完成八隅体
示例:硝酸根阴离子 NO3-
- N = 4 个原子 x 8 个电子 = 32
- V = 5 + 6 + 6 + 6 + 1 = 24 (N + O + O + O + 电荷)
- S = 32-24 = 8 个共享电子 = 4 个键
- 孤对数由差值获得:(V-S)/2 = (24-8)/2 = 8
- 现在绘制分子,从四个键开始,然后添加八个孤对以完成八隅体
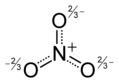
- 计算硝酸根阴离子中每个原子周围的共享电子和非共享电子,你会发现所有原子都处于八隅体状态,并且价电子总数 (V) 为 24。如果你按照上述规则进行 N-V 计算,你应该始终得到一个八隅体结构。

形式电荷分布是通过将共享(键合)电子平均分配给原子来确定的。因此,单键 O 原子各自拥有 7 个电子,因为 O 位于第 6 族,所以它们的正式电荷为 -1。双键 O 的正式电荷为零。N 原子的正式电荷为 +1,因为它“拥有” 4 个价电子,并且位于第 5 族。
请注意,形式电荷与氧化数(或氧化态)不同。在硝酸根阴离子中,氮的氧化态为 +5,氧的氧化态为 -2。形式电荷通常更接近原子上的“真实”电荷(例如,通过X 射线光电子能谱测量)。氧化态是跟踪氧化还原反应的有用记账工具,我们将在第四章中讨论。与氧化态一样,分子或离子中原子上的形式电荷必须加起来等于其总电荷。
我们可以类似地绘制氨的 Lewis 结构,如下所示
当我们将共享电子平均分配给原子时,我们看到 N 原子有五个电子,每个 H 原子有一个电子。这些与它们的族号相同,因此,氨分子中的所有形式电荷都为零。
下面显示了路易斯酸碱加合物 NH3BF3、水合氢离子 H3O+ 和硫酸根阴离子 SO42- 的八隅体结构。在这种情况下(以及我们绘制的许多路易斯结构中),我们省略了周围原子周围的隐含孤对。尝试使用 N-V 方法计算这些分子中每个分子的键数,并补充那些没有明确绘制的孤对。
在可能存在多个价键结构的情况下,我们可以使用形式电荷来判断哪个结构应该更稳定或更不稳定。规则如下:
- 稳定结构中原子上的形式电荷最小化,零是最理想的情况。
- 负形式电荷应放在最具电负性的原子(s) 上。
- 正形式电荷应放在最不具电负性的原子(s) 上。
- 在分子中将类似电荷 (++ 或 --) 放在相邻原子上的做法是不利的。
下面显示了这些规则在 BF3 和 ONF 的替代结构中的示例。


海洋之外的生命的存在归功于平流层中臭氧 (O3) 的存在。臭氧吸收太阳光谱中的紫外线,否则会对 DNA 和其他生物分子造成灾难性的损害。由于臭氧是由 O2 光化学产生的,而 O2 本身是由光合作用产生的,因此遥远行星大气中臭氧的光谱特征是寻找地外生命的一种可能方法。 
苏珊·所罗门 发现了臭氧被氯氟烃(氟利昂)分解的异质催化机制,形成了南极臭氧洞。她的工作为《联合国蒙特利尔议定书》奠定了基础,该议定书是一项国际协议,通过规范有害化学物质来保护臭氧层。
在 BF3 的情况下,左侧的结构是非八隅体的,因为 B 的价电子层中只有六个电子(三个键)。这种结构被称为电子缺陷。可以绘制八隅体结构(右侧),但它在 F 上放置了一个正形式电荷,F 是分子中最具电负性的原子。因此,两种结构都不是完全“快乐”的,但形式电荷规则告诉我们,左侧的电子缺陷结构更稳定。BF3 的电子缺陷使其成为一种强大的路易斯酸。
在 ONF 的情况下,左侧的结构有两个原因不利。首先,它在 F 上放置了一个正形式电荷,F 是最具电负性的原子。其次,还有另一种可能的结构(右侧),该结构的形式电荷为零,这比具有非零电荷的结构更可取。这意味着右侧的结构(在 N 和 O 之间具有双键)更合理。
共振结构
臭氧 (O3) 分子具有两个等效的八隅体结构,如下所示:
在这两种情况下,路易斯点图表明分子中存在三种氧原子,其形式电荷分别为 +1、0 和 -1。这些结构还表明臭氧应该有一个单键和一个双键。然而,通过实验(通过 电子衍射),我们发现该分子是对称的,两个 O-O 键长相同。真实的(瞬时)结构是两种形式的平均值,如下所示。在该分子的经典路易斯图中,我们可以通过观察电子比原子核轻几千倍,因此在分子振动的时标上移动速度非常快来合理化共振。因此,在氧原子调整其位置所需的时间内,电子可以来回移动多次。在量子力学 MO 图(第二章)中,我们将看到共振涉及完全在分子中的原子之间离域的电子。我们用双箭头表示共振结构,以表示路易斯结构之间唯一的区别是电子的分布。
在臭氧的瞬时结构中,形式 (-) 电荷在两个末端氧原子之间共享,因此每个氧原子的形式电荷为 -1/2。O-O 键是单键和双键的平均值,即每个 O-O 键级为 1.5。

类似地,硝酸根阴离子具有三个共振结构,并且通过实验(通过硝酸盐的 X 射线晶体学)我们发现离子中所有的 N-O 键都是相同的。在这种情况下,在平均结构中,每个 O 原子的形式电荷为 -2/3,N-O 键级为 4/3 (=1.33...)。

不等价的共振结构
共振规则也适用于不等价结构,这些结构通常彼此具有不同的能量。在这种情况下,分子的结构代表低能量结构的加权平均值。一个很好的例子是氰酸根离子 OCN-。我们可以为该分子写出三个不等价的八隅体结构:
前两个是合理的共振结构,尽管我们怀疑左侧的结构是最好的,因为它将负形式电荷放在最具电负性的原子。最后一个结构显然是一个糟糕的共振结构,因为形式电荷很高,并且氧原子带正电荷。因此,真实的结构是前两个结构的加权平均值。
无键共振
一种有趣且有用的不等价共振结构是在两个原子之间具有零键级。这种无键共振的概念对于理解许多含卤素和含氢化合物的键合非常重要。该概念在下面针对通用分子 X-Y-Z 进行说明,其中 Z 可以是诸如 F 之类的电负性卤素原子。通过将键合电子从 Y-Z 键移动到 Z 原子上,并将孤对从 X 移动到 X-Y 键中,我们生成了右侧所示的共振结构,其中所有原子都保持八隅体,但 Y 和 Z 之间没有键。

重要的是要认识到在这个例子中,无键形式只是一个共振结构,因此 Z 原子仍然与 Y 键合。如果这两个共振结构在这个例子中具有相同的能量,我们预计 X-Y 键级为 1.5,Y-Z 键级为 0.5。因此,Y-Z 键应该比键级为一的化合物中的键长,并且应该相对容易断裂 Y-Z 键。
下面显示了无键共振的一些分子例子。在 ONF3 分子中,N-F 键比 NF3 中的 N-F 键长得多,在 NF3 中,键级为 1。这可以通过右侧显示的无键共振形式来解释。类似地,在通过将 BH3 与 CO 相结合形成的路易斯酸碱加合物中,我们可以使用将部分正电荷放在 H 原子上的无键共振形式来解释长的 B-H 键。

无键共振通常用于为所谓的超价化合物提供八隅体键合图,这些化合物似乎在中心原子的键合壳层中具有超过 8 个价电子。例如,我们可以考虑三碘离子 I3- 的两种不同的价键结构,该离子是通过 I- 与 I2 在水中反应形成的:


在这个结构中,中心碘原子在其价电子层中具有 10 个电子,违反了八隅体规则。拉曼光谱表明三碘离子的 I-I 键比 I2 中的 I-I 单键弱,这表明这种图不是对键合的准确描述。可以使用无键共振结构来获得 I3- 的更好表示,如下所示。我们将看到这种图与第二章中 I3- 的 MO 描述是一致的。
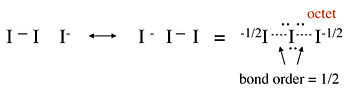

我们可以为 XeF2 分子绘制类似的图,该分子具有与 I3- 相同数量的价电子。这种图与 XPS 数据一致,XPS 数据显示 F 原子带部分负电荷,以及振动光谱,振动光谱表明 XeF2 中的 Xe-F 键比单键阳离子 Xe-F+ 中的 Xe-F 键弱。

其他众所周知的超价化合物包括 PF5、P(CH3)5 和 SF6,以及含氧酸,如 H2SO4 和 HClO4。这些分子的超价结构通常被画出来,并解释说中心原子的 d 轨道参与了成键,形成 5 配位和 6 配位分子分别的 dsp3 和 d2sp3 杂化轨道。然而,真实的分子轨道计算表明,磷和硫的 3d 轨道能量太高,无法显著参与 PF5 和 SF6 中的成键。对于这些分子,我们可以使用无键共振来构建合理的八隅体结构,预测中心原子和 F 之间的极性键。


在其他情况下,例如 P(CH3)5,八隅体结构不合理,因为它表明 P 和 C 之间存在极性键,且 C 带有部分负电荷。此外,在含氧酸,例如 H2SO4 和 HClO4 的情况下,X 射线晶体学数据表明,与氢原子不键合的氧原子上的 S-O 和 Cl-O 键更短,这与超价结构更一致。

超价和八隅体规则是否真正有效地描述了这些化合物中的成键问题,已经在许多计算研究中进行了探讨,这些研究使用越来越精确的量子力学计算来确定与中心原子相关的电子数。在 2002 年的一项研究中,Gillespie 和 Silvi[4] 发现,对于具有正电性配体的化合物,例如 P(CH3)5,价层电子数大于 8,而对于像 PF5 这样的化合物,价层电子数小于 8。他们得出结论,这些价层电子壳层电子数主要取决于中心原子及其配体的配位数和电负性,并且超价分子和非超价分子(路易斯八隅体)之间的成键没有本质区别。这提醒我们,八隅体规则不是自然规律,而是一个在一定范围内有效的经验规则。

等电子原理
在使用 N-V 方法计算分子的八隅体结构时,我们只需要知道原子数和电子数,而不需要知道原子的具体种类。这意味着对于包含以下条件的任何分子或离子,我们都会得到相同的答案(以及相同的八隅体和共振结构):(a) 具有相同数量的非氢原子,以及 (b) 具有相同的总价电子数。这类分子被称为等电子分子。这是一个强有力的结论,因为一旦我们确定了一个分子的电子结构,我们就可以为所有其他等电子分子写出相同的解。例如,我们在上面已经注意到,I3- 和 XeF2 都有 22 个价电子,它们具有相同的价键结构。我们还可以预期等电子分子具有相同的形状,并且通常具有相似的物理性质。
以下四个分子和离子都包含三个非氢原子和 16 个价电子。它们都是具有两个双键的直线形分子。以下所示的四个分子和离子都包含四个非氢原子和 24 个价电子。这四个分子具有三角形平面结构。虽然 BF3 是这个等电子系列的成员,但我们不将其写成包含 B=F 双键的共振形式,因为这会导致 F 上带有正形式电荷。
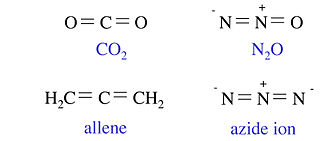

类似地,我们可以证明 CH4、NH3、NH4+、H2O、H3O+、HF、F- 和 OH- 都与一个非 H 原子和八个价电子等电子。在下一节中,我们将看到这导致了这些分子几乎相同的电子形状。

等电子固体。等电子原理不仅适用于分子,也适用于扩展的固体。一组具有技术重要性的等电子固体是 p 区半导体。第 14 族元素 Si 是最广泛使用的电子半导体,但正如我们将在后面讨论的那样,它不是一个好的发光体。用于激光、高效率照明和显示技术的 LED(发光二极管)是由与 Si 和 Ge 等电子的化合物制成的,特别是 GaAs、GaP、AlAs 和 GaN(每个原子都包含四个价电子)。CdTe 和 CuIn1-xGaxSe2 (CIGS) 是很有前途的太阳能电池材料,它们也具有相同数量的价电子。与 Si 和 Ge 一样,这些化合物在固态下具有四面体键合结构,并吸收了大部分太阳光谱的光,正如我们将在第 8 章和第 10 章中更详细地讨论的那样。
等电子原理也是材料研究中一个强大的工具,因为它为寻找具有相似甚至改进性质的新材料提供了指导。例如,发现可以用 CsSnI3[5] 制造 8.5% 效率的薄层太阳能电池,促使人们探索许多具有相同钙钛矿晶体结构的等电子 ABX3 化合物。最近,基于该结构家族中光吸收剂的薄膜太阳能电池(MA)PbI3-xClx 和 FAxMA1−xPbBryI3−y(MA+ = 甲胺,CH3NH3+;FA+ = 甲酰胺,HC(NH2)2+)被报道,其效率高达 22%。[6][7][8]
1.2 分子的形状(VSEPR 理论)和轨道杂化
[edit | edit source]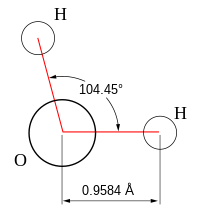
价层电子对互斥理论 (VSEPR) 是一种简单且有效的方法,可以预测和解释分子的形状。该理论基于最小化电子对之间的静电排斥的概念,正如 Sidgwick 和 Powell 在 1940 年首次提出的那样,[9] 然后由 Gillespie 和 Nyholm 在 1957 年推广,[10] 并在此后的 50 多年中被广泛应用。 [11]
为了使用 VSEPR 模型,首先需要使用路易斯点图来确定中心原子周围的孤对数和成键域数。因为 VSEPR 将所有成键域视为相等(即,单键、双键和半键都算作一个电子域),所以可以使用八隅体结构或超价结构,只要孤对数(在两种结构中应该相同)被正确计算即可。例如,在上述 I3- 离子的超价结构或八隅体结构中,中心 I 原子上都有三个孤对和两个成键域。然后,我们按照以下步骤来获得电子几何形状
- 确定分子中中心原子的孤对数,并加上成键原子的数量(也称为成键域)。
- 这个数字(空间数)通过最小化排斥来定义分子的电子形状。例如,空间数为 3 会形成一个三角形平面电子形状。
- 电子域之间的角度主要由电子几何形状决定(例如,空间数为 4 时为 109.5°,这意味着电子形状为四面体)。
- 这些角度通过排斥力的等级进行调整:(孤对 - 孤对)>(孤对 - 键)>(键 - 键)。
分子几何形状从电子几何形状推断而来,将孤对视为存在但不可见。确定分子结构最常用的方法——X 射线衍射、中子衍射和电子衍射——很难看到孤对,但它们可以准确地确定原子间键长和键角。
下表列出了空间数为 2 到 9 的电子形状和分子形状示例。我们最常关注的是空间数为 2 到 6 的分子。
| 成键电子对 | 孤对 | 电子域(空间数) | 形状 | 理想键角(示例中的键角) | 示例 | 图像 |
|---|---|---|---|---|---|---|
2
|
0
|
2
|
180°
|
|||
3
|
0
|
3
|
120°
|
|||
2
|
1
|
3
|
120°(119°)
|
|||
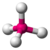
4
|
0
|
4
|
109.5°
|
|||
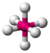
3
|
1
|
4
|
109.5°(107°)
|
|||
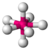
2
|
2
|
4
|
109.5°(104.5°)
|
|||
5
|
0
|
5
|
90°、120°、180°
|
|||
4
|
1
|
5
|
180°、120°、90°(173.1°、101.6°)
|
|||
3
|
2
|
5
|
90°、180°(87.5°、< 180°)
|
|||
2
|
3
|
5
|
180°
|
|||
6
|
0
|
6
|
90°、180°
|
|||
5
|
1
|
6
|
90°(84.8°)、180°
|
|||
4
|
2
|
6
|
90°、180°
|
|||
7
|
0
|
7
|
90°、72°、180°
|
|||
6
|
1
|
7
|
72°、90°、144°
|
XeOF5−
|
||
5
|
2
|
7
|
72°、144°
|
|||
8
|
0
|
8
|
||||
9
|
0
|
9
|
从表中我们可以看到,一些作为示例的分子具有偏离理想电子几何形状的键角。例如,氨分子中的 H-N-H 键角为 107°,水分子中的 H-O-H 键角为 104.5°。我们可以用上面的最后一条规则来解释这一点。氨中的孤对电子对 N-H 键中的电子产生更大的排斥作用,比键之间相互排斥更大。在水分子中,由于存在两个孤对电子,这种孤对电子排斥作用会产生更大的空间影响。类似地,在“跷跷板”分子 SF4 中,轴向 F-S-F 键角由于分子中孤对电子的排斥作用而略小于 180°。
几何异构体
对于表中的一些分子,我们注意到,存在多种可能的形状可以满足 VSEPR 规则。例如,XeF2 分子具有 5 的空间数和三角双锥几何形状。存在三种可能的立体异构体:一种是 F 原子占据轴向位置,导致形成线性分子,一种是 F 原子占据一个赤道位置和一个轴向位置(导致 90° 的键角),另一种是 F 原子都位于赤道位置,F-Xe-F 键角为 120°。

XeF2 的观察到的几何形状是线性的,这可以通过考虑用于形成轴向和赤道位置的键(或孤对电子)的轨道来解释。存在四个可用的轨道,s、px、py 和 pz。如果我们选择 z 轴作为轴向方向,我们可以看到 px 和 py 轨道位于赤道平面。我们假设球形的 s 轨道被分子中的五个电子域平均共享,两个轴向键共享 pz 轨道,三个赤道键共享 px 和 py 轨道。然后我们可以计算轴向和赤道 F 原子的键序如下
轴向:1/5 s + 1/2 pz = 0.7 键(形式电荷 = -0.3)
赤道:1/5 s + 1/3 px + 1/3 py = 0.867 键(形式电荷 = -0.133)
由于氟比孤对电子更具电负性,它更喜欢轴向位置,在那里它将具有更负的形式电荷。一般来说,根据这种推理,孤对电子和像 CH3 这样的正电性配体在三角双锥几何形状中总是更喜欢赤道位置。像 F 这样的负电性配体总是会占据轴向位置。
在 BrF4- 阴离子(与表中的 XeF4 等电子)的情况下,电子几何形状是八面体形的,存在两种可能的异构体,其中两个孤对电子彼此为顺式或反式。在这种情况下,孤对电子-孤对电子排斥作用占主导地位,我们获得了孤对电子的反式排列,从而形成了平面正方形分子几何形状。

轨道杂化
观察到上述各种电子形状的分子,乍一看,与我们对原子轨道的认识相矛盾。对于像氧这样的原子,我们知道 2s 轨道是球形的,而 2px、2py 和 2pz 轨道是哑铃形的,并且沿着笛卡尔坐标轴指向。水分子包含两个与氧原子相连的氢原子,它们并非以 90° 的角度相连,而是以 104.5° 的角度相连。考虑到原子轨道的相对取向,我们如何得到 104.5°、120° 等电子域之间的角度?为了理解这一点,我们需要了解一些关于原子和分子中电子的量子力学知识。
原子轨道 ψ 代表薛定谔方程的解,
这里 E 是轨道中电子的能量,而 是哈密顿算符。
与经典力学类似,哈密顿算符通常表示为对应于系统的算符的动能和势能之和,形式为
其中 是势能,并且
是动能算符,其中m是粒子的质量,动量算符为
- 其中
这里 是 h/2π,其中 h 是普朗克常数,拉普拉斯算符 ∇2 为
虽然这并非经典力学中哈密顿量的技术定义,但它是它在量子力学中最常见的形式。将这些结合在一起就会得到薛定谔方程中使用的熟悉形式
对于类氢(单电子)原子,薛定谔方程可以写成
其中Z为核电荷,e为电子电荷,r为电子的位置。等式右侧的径向势项是由于库仑相互作用,即原子核和电子之间的静电吸引,其中ε0是介电常数(自由空间的介电常数),并且
是质量为mn的原子核和质量为me的电子的二体约化质量。近似地,µ ≈ me。

这就是埃尔温·薛定谔在 1926 年著名的推导出的方程,用于求解类氢原子中 s、p、d 和 f 原子轨道的能量和形状。对于物理学和化学来说,这是一个巨大的概念飞跃,因为它不仅解释了氢原子的量子化能级,而且还为八隅体规则和元素在周期表中的排列提供了理论基础。
如果我们将适当的势能函数 V(r,t) 代入哈密顿量,薛定谔方程可以用来描述比氢原子更复杂的化学体系(例如多电子原子、分子、无限晶体以及这些体系的动力学)。在这些情况下,数学变得更加复杂,必须用数值方法求解方程,所以为了我们的目的,我们将坚持最简单的情况:时间不变、单电子、类氢原子。

在不深入讨论薛定谔方程的太多细节的情况下,我们可以指出它的一些最重要的性质
- 该方程源于这样一个事实:总能量 (E) 是动能 (KE) 和势能 (PE) 的总和。这三个量在数学上用方程中的算符表示。
- 在方程的左侧,总能量算符 (E) 是一个标量,它乘以波函数 ψ。ψ 是空间坐标 (x,y,z) 的函数,它与电子在空间中该点的概率相关。
- 方程右侧的第一项表示动能 (KE)。动能算符与 ∇2(拉普拉斯算符)成正比,它对 ψ 进行二阶导数(关于三个空间坐标)。因此,薛定谔方程是一个微分方程。
- 方程右侧的第二项表示库仑势 (PE),即带正电的原子核和带负电的电子之间的吸引力。
- 薛定谔方程的解是一组能量 E(它们是标量)和波函数(也称为原子轨道)ψ,它们是空间坐标的函数。您有时会看到能量被称为特征值,轨道被称为特征函数,因为在数学上,薛定谔方程是一个特征函数-特征值方程。虽然 ψ 是坐标的函数,但 E 不是。因此,处于 2pz 轨道的电子无论在空间中的什么位置,其总能量 E (= PE + KE) 都是相同的。
- 这些 E 值及其相关的波函数 ψ 是根据它们的量子数 n, l, 和 ml 进行分类的。也就是说,微分方程有许多解,并且每个解 (ψ(xyz) 和 E) 都有一组唯一的量子数。一些轨道集是简并的,这意味着它们具有相同的能量(例如,2px、2py 和 2pz)。
- 薛定谔方程的解 ψ(xyz)(例如 1s、2s、2px、2py 和 2pz 轨道)代表在空间中特定点 (x,y,z) 找到电子的概率幅度。概率幅度可以是+ 号或 - 号。我们通常用 2p 轨道的两个叶片上的阴影或 + 和 - 符号来表示不同的符号。
- 概率振幅的平方,ψ2,始终为正数,表示在空间中 x,y,z 点找到电子的**概率**。因为找到电子的总概率为 1,所以波函数必须进行**归一化**,使得 ψ2 在空间坐标(从 -∞ 到 +∞)上的积分等于 1。
- 薛定谔方程的解是**正交**的,这意味着任意两个解的乘积(在整个空间上积分)都为零。例如,2s 和 2px 轨道的乘积,在空间坐标从 -∞ 到 +∞ 上积分,结果为零。
轨道杂化涉及对作为薛定谔方程解的原子轨道进行线性组合。从数学上来说,这是通过认识到薛定谔方程是一个线性微分方程来证明的。因此,薛定谔方程解的任何求和也是一个有效的解。然而,我们仍然需要限制条件,即我们的杂化轨道必须是**正交**的并且是**归一化**的。
轨道杂化的规则
对于**sp 杂化**,例如 BeF2 或 CO2 分子,我们对 2s 和 2pz 轨道(将 z 作为 Be-F 键的轴)进行两个线性组合
这里我们只是将 2s 和 2pz 轨道加减起来;我们将证明这两个轨道都是归一化的(即 ∫ψ12dτ = ∫ψ22dτ = 1)并且是正交的(即 ∫ψ1ψ2dτ = 0)作为练习留给感兴趣的读者。
这在物理上意味着什么在下图中解释。通过结合 2s 和 2pz 轨道,我们创造了两个沿 z 轴指向的具有较大叶瓣(高电子概率)的新轨道。这两个轨道是简并的,并且能量介于 2s 和 2pz 轨道之间。

对于一个孤立的 Be 原子,它有两个价电子,最低能量状态将有两个电子在 2s 轨道上自旋配对。然而,这些电子将无法用于成键。通过将这些电子**提升**到简并的 2spz 杂化轨道,它们变得未配对,并准备与 BeF2 中的 F 原子成键。如果**成键能量**(在提升状态下)超过了提升能量,则这种情况将会发生。**总成键能量**,即 Be 原子在其基态与两个 F 原子结合时释放的能量,是成键能量和提升能量之间的差值。
我们同样可以从一个 2s 和两个 2p 原子轨道构建**sp2 杂化轨道**(例如,对于 BF3 分子或 NO3- 阴离子)。以分子平面为 xy 平面,我们得到了三个杂化轨道,它们彼此之间的夹角为 120°。三个杂化轨道分别是

这些轨道再次是简并的,它们的能量是 2s、2px 和 2py 原子轨道能量的加权平均值。
最后,为了形成 sp3 杂化轨道,例如在 CH4、H2O 等分子中,我们将所有四个 原子轨道组合起来形成四个简并的杂化轨道


sp3 杂化轨道 的叶瓣指向四面体 (或立方体的交替角),这与 CH4 中的四面体键角以及 NH3 和 H2O 中接近四面体的角度相一致。同样,我们可以证明,我们可以通过构造 sp 和 sp2 杂化来构建三角双锥电子形状,以及从三组 sp 杂化构建八面体几何形状。由此产生的图像是,原子轨道可以根据最能使电子对排斥最小化的形状进行杂化。

然而,有趣的是,PH3、H2S 和 H2Se 中的键角接近 90°,这表明 P、S 和 Se 主要在这些分子中使用它们的 p 轨道与 H 形成键。这与周期表中 s 和 p 轨道之间的能量差在下降过程中大致保持不变这一事实一致,但键能随着价电子离原子核越来越远而减小。因此,在周期表中第三、第四和第五行的元素的化合物中,使用 s-p 轨道杂化在成键中的趋势下降。对于这些较重的元素,键能不足以抵消将 s 电子提升到 s-p 杂化轨道所需的能量。

莱纳斯·鲍林 在 1932 年提出了电负性的概念来解释具有极性键的分子额外的稳定性。[12] 原子的电负性,用希腊字母 χ 表示,可以定义为原子在化学键中吸引电子的趋势。在鲍林标度上,两个原子 A 和 B 之间的电负性差被定义为解离能 Ed 的 A-A、B-B 和 A-B 键
其中能量以电子伏特表示。
这个定义,虽然直接与化学键的强度相关,但需要来自许多化合物的热化学输入数据,其中一些数据在当时不可用。Mulliken[13][14] 以及后来的 Pearson[15] 开发了一个基于自由 A 和 B 原子的电子亲和能和电离能平均值的电负性标度,他们将此标度与热化学数据和鲍林标度相关联。
在鲍林标度上,电负性最小的元素是碱金属 (χ = 0.7-1.0),电负性最大的元素是氧 (3.5) 和氟 (4.0),位于周期表的上右侧。碳和氢的电负性介于两者之间 (分别为 2.6 和 2.2,以鲍林标度为单位)。总体趋势 (见下表) 是电负性在周期表中向上和向右移动时增加。这种行为有一些有趣的例外,最值得注意的是在过渡系元素底部出现了两个高电负性岛,在钨 (χ = 2.4) 和金 (χ = 2.5) 处达到峰值。第一个可以解释为 Mo 和 W 等元素的金属 - 金属键能非常高,它们可以在成键中使用所有六个价电子,正如我们在第 6 章中讨论的那样。然而,第二个发生在 Pt 和 Au 等键合较弱的贵金属中,这会导致它们在活性系列中的位置较低,[16] 以及它们作为催化剂的非凡性质。

键的极性由电负性差决定。作为指南,我们将键定义为
- 离子键 如果 Δχ > 2.0
- 极性键 如果 2.0 > Δχ > 0.5
- 非极性键 如果 0.5 > Δχ
键的极性有助于我们理解分子之间的非共价力,例如氢键和偶极 - 偶极相互作用。它还有助于我们解释分子的反应性。例如,Si-H 键 (χSi = 1.8, χH = 2.1) 比 C-H 键 (χC = 2.5, χH = 2.1) 更像氢化物。因此,硅烷与酸反应生成 H2,而膦 (χP = 2.1) 和烃则不会。同样,亲电取代反应在 Si-H 和 P-H 化合物上比在 C-H 化合物上更容易发生。
化学键的强度也与键长相关,键越长,由于轨道重叠较弱,键越弱。鲍林提出了一个将键长与键强度相关联的经验公式。对于给定的一对原子(例如,两个碳原子)
- D(n) = D(1) - 0.6 log10(n)
其中 D(n) 代表以 Å 为单位的键长,n 是键级。在这种情况下,D(1) 将是 C-C 单键的长度,我们可以从烷烃中的平均键长 (1.54 Å) 获得。使用这个公式,我们可以预测乙烯 (C=C 双键) 和乙炔 (C≡C 三键) 中的键长应该分别为 1.36 和 1.25 Å,这与实验值 1.33 和 1.20 Å 接近。在相关形式中,鲍林公式可用于计算当单键长度 D(1) 不可用时的键长
- D(n) = D(m) - 0.6 log10(n/m)
这里 n 和 m 代表同一类原子之间的两个不同的键级。这告诉我们,例如,三键和双键之间的长度差,D(2)-D(3),应该为 - 0.6 log10(2/3) = 0.11 Å。

一些键长和键能是异常的。例如,F2 中的 F-F 键长为 1.43 Å,比 F 原子共价半径的两倍 (0.64 Å) 长 0.15 Å。F-F 键也相当弱 (键解离能 = 155 kJ/mol),相对于 Cl-Cl 键 (242 kJ/mol)。通过将额外的键长代入 Pauling 公式,我们计算出 F2 分子中的键级仅为 0.6,即比 F-F 单键弱得多。造成这种情况的物理原因是 F-F 键因 F 原子上孤对电子的排斥而“拉伸”。这种拥挤是由于 [He] 1s2 内层轨道以及氟原子的价轨道都被高核电荷收缩造成的。相反,Cl2 中的 Cl 原子具有更大的 [Ne] (1s22s22p6) 内层,因此 Cl-Cl 具有“正常”的单键键长 (1.98 Å),是 Cl 原子共价半径的两倍 (0.99 Å)。类似的孤对电子排斥效应解释了肼 (H2N-NH2) 和过氧化氢 (HO-OH) 中异常长且弱的 N-N 和 O-O 单键,这两种分子都是高反应性分子。
比较键强趋势时,电负性差异和孤对电子排斥的重要作用很明显。下表显示了 p 区元素与 H 和 F 的平均单键焓。H 与第二周期元素 (C、N、O、F) 形成的键比与第三周期元素 (Si、P、S、Cl) 形成的键更强,因为 2p 价电子更靠近原子核,因此比 3p 轨道中的电子形成更强的键。与 H 的键也遵循预期的趋势,即随着电负性差异的增加,键强度增加。然而,第二周期元素 (C、N、O、F) 与 F 之间的键由于孤对电子排斥而异常弱。因此,Si-F 键明显强于 C-F 键,而 C-H 键远强于 Si-H 键。强 Si-F 键是 HF 蚀刻玻璃 (产生 SiF62- 阴离子) 的原因,而强 C-H 键是烃类和其他有机分子稳定性的重要因素。
平均 E-H 和 E-F 键焓 (kJ/mol)
| C-H 413 | N-H 391 | O-H 483 | H-F 567 |
| Si-H 323 | P-H 322 | S-H 339 | H-Cl 431 |
|
|
|||
| C-F 485 | N-F 272 | O-F 190 | F-F 155 |
| Si-F 565 | P-F 490 | S-F 327 | Cl-F 253 |

F2 中异常弱的键是氟高电负性以及元素氟气具有传奇反应性的原因,氟气与氢和金属粉末发生爆炸性反应。由于元素氟的不稳定性及其与更具电正性的元素形成的键的极性,氟化合物往往非常稳定。例如,稀有气体 Xe 和 Kr 与氟反应形成共价化合物,而其他卤素则不反应。氟碳化合物含有强 C-F 键,具有很高的热稳定性和化学稳定性。全氟碳化合物如 特氟龙 (聚四氟乙烯,-(CF2CF2)n-,PTFE) 也是高度疏水的。全氟碳的非凡疏水性源于 -CF2- 和 -CF3 基团比 -CH2- 和 -CH3 基团“更胖”;因此,将它们溶解在水中比溶解烃类更能破坏氢键网络。 [21]
1.4 讨论问题
[edit | edit source]小组论文项目
加入无机化学课程中的一组同学。每个小组应有 3 或 4 名学生。安排时间见面一个小时左右。在会议之前,阅读第一部分 (第 1367-1391 页) 以及 Linus Pauling 关于化学键本质的 文章 (J. Am. Chem. Soc. 1931, 53, 1367-1400) 结尾处的摘要。
这篇文章是在薛定谔发展原子轨道的量子力学理论仅仅几年后发表的,被认为是现代化学史上最重要的文章之一。在会议上,讨论以下问题:(1) 在 Pauling 发表这项工作之前,人们对分子中的化学键了解多少?(2) 这篇论文引入了哪些我们今天仍在使用的概念?(3) 这些想法为什么重要?(4) Pauling 有没有犯错,如果有,是什么,为什么?
与你的同学一起,写一篇 1-2 页的论文来回答这些问题。请在首页上列出你小组中所有学生的姓名;你们所有人将在这项作业中获得相同的成绩。将从这些论文中摘录一些匿名片段与全班同学分享。
本章中的课堂讨论问题
- 什么是等效共振结构?用一些上面没有涉及的新例子来说明。
- 用一些新的例子解释无键共振和超价键。
- 对于含有奇数电子的分子,价键理论有哪些局限性?用一两个例子说明。
1.5 习题
[edit | edit source]1. 为以下物质绘制组合八隅体结构(包括形式电荷、键级和分子形状):(a) BrO3-、(b) SF6、(c) KrF2、(d) HClO4 (= HOClO3)、(e) NO2- 和 (f) ClO2。
2. 为以下物质绘制组合八隅体结构(包括形式电荷、键级和分子形状):(a) Al2Cl6、(b) SnCl3-、(c) BrF4-、(d) HOClO、(e) SO3 和 (f) NO2+。
3. 使用共振来显示为什么甲酰胺 (HCONH2) 中的 CO 键距比丙酮中的 CO 键距更长。
4. 给出与氨气等电子结构的五种稳定分子和/或离子的公式。
5. 命名三种与 (a) NO2+、(b) BF4-、(c) CH4 和 (d) HCN 等电子的知名分子或离子。
6. 命名三种与 (a) CN-、(b) H2O、(c) BF3 和 (d) CO2 等电子的知名分子或离子。
7. 乙炔中的 CC 键距为 1.20 Å。使用 Pauling 键长-键强度公式,D(n) = D(1) - 0.6 log(n),估计乙烯酮 (H2CCO) 中的 C-C 键距。
8. 在羟胺 H2NOH 中,N-O 键距为 1.46 Å。使用 Pauling 键长-键强度公式,估计 NO2 和 NO3- 中的 N-O 键距。
9. 氮可以在含有如 NF4+ 和 NO3- 等离子的化合物中以 +5 氧化态存在。然而,中性二元化合物 NF5 是未知的。你能为这些化合物中的每一个画出八隅体结构吗?为什么 NF5 会不稳定?
10. 考虑化合物 NH3 和 PH3。氨中 H-N-H 键角为 108o (接近四面体角,109.5o),但 PH3 中的类似角度为 93o。为什么 PH3 中的角度更接近 90o 而不是四面体角?
11. N2F3+ 离子的两种假设结构为 [N-NF3]+ 和 [F-N-NF2]+。哪个更稳定?解释。(注意:公式中的线可以表示单键或多键)
12. 二氟化氪 KrF2 在干冰温度下分解成 Kr 和 F2。然而,[KrF]+ 离子的几种盐相对稳定。为 KrF2 和 [KrF]+ 绘制价键图,显示孤对电子、可能的共振结构、形式电荷、键级和键角。为什么 [KrF]+ 比 KrF2 更稳定?
13. 考虑阴离子 SF3O2- (其中 S 为中心原子)。可能存在多少种异构体?哪一种最稳定?
14. 卤素间化合物 BrF 中的 Br-F 键距为 1.76 Å。使用此信息估计 BrF3 和 BrF5 中的平均键长。
15. BH3 和 BH4- 中的 B-H 键距大致相同。然而,BF3 中的 B-F 键距比 BF4- 离子中的 B-F 键距短。解释。
16. 肼 (H2N-NH2) 中的 N-N 键解离能为 159 kJ/mol。N2 中的 N-N 三键解离能为 941 kJ/mol,即远大于肼中 N-N 单键解离能的三倍。解释为什么肼中的 N-N 键如此弱,以及为什么这种效应在 N2 中没有出现。
17. 证明一组四个 sp3 杂化轨道满足以下条件:(a) sp3 集中任意两个轨道都是正交的,以及 (b) 轨道是适当地归一化的。
18. 在量子力学中,沿特定方向 (例如 x 方向) 运动的粒子的动量 (p) 可以通过对它的波函数 进行 动量算符 操作来获得
- ,其中
知道这个算子的正确形式是薛定谔提出哈密顿算子的关键,该算子作用于波函数得到总能量。动量算子也必须与德布罗意关系p = h/λ一致,该关系将动量与粒子波长联系起来。
类比电磁波,薛定谔知道在x方向上自由空间中运动的类波粒子(如电子)可以用波函数描述
其中波数k与粒子的德布罗意波长λ成反比,由k = 2π/λ给出。这里A是归一化常数,ω是波的频率,表示其相位。
使用动量算子证明对于自由粒子,我们从得到的动量值p与德布罗意关系p = h/λ一致。
(提示:k、ω和与x无关)
19. N3S4+是一个环状阳离子,不含N-N键。绘制七元环的结构,并使用电子计数方法确定单键、双键和孤对电子的数量。绘制该离子可能的共振结构,显示形式电荷,并指出哪个结构最稳定。
20. F的电负性高于Cl,F2的氧化性远强于Cl2,尽管氟的电子亲和能(-328 kJ/mol)低于氯(-349 kJ/mol)。解释这种明显的矛盾。
21. 甲烷 (CH4)、氨 (NH3) 和水 (H2O) 中的单键分别比SiH4、PH3和H2S中的单键强。类似的含氟化合物遵循相反的趋势:CF4、NF3和OF2中的单键比SiF4、PF3和SF2中的单键弱。你能解释这两种相反的趋势吗?
1.6 参考文献
[edit | edit source]- ↑ G. N. Lewis, "The atom and the molecule," J. Am. Chem. Soc. 1916, 38, 762-785
- ↑ W. Saenger, "The structure of the blue starch-iodine complex," Naturwissenschaften 71, 31-36 (1984).
- ↑ R. D. Hancock and B. J. Tarbet, "The other double helix - the fascinating chemistry of starch," J. Chem. Ed. 77, 988-992 (2000).
- ↑ R. J. Gillespie and B. Silvi, "The octet rule and hypervalence: two misunderstood concepts," Coord. Chem. Rev. 233-234, 53-62 (2002).
- ↑ I. Chung, B. Lee, J. He, R. P. H. Chang and M. G. Kanatzidis, All-solid-state dye-sensitized solar cells with high efficiency, Nature 485, 486-489 (2012). doi:10.1038/nature11067
- ↑ S.D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza, and H. J. Snaith, Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber, Science 342, 341-344 (2013). DOI: 10.1126/science.1243982
- ↑ G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar, and T. C. Sum, Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3, Science 342, 344-347 (2013). DOI: 10.1126/science.1243167
- ↑ J.-P. Correa-Baena, A. Abate, M. Saliba, W. Tress, T. J. Jacobsson, M. Grätzel, and A. Hagfeldt, The rapid evolution of highly efficient perovskite solar cells, Energy Environ. Sci., 10, 710-727 (2017). DOI: 10.1039/C6EE03397K
- ↑ N. V. Sidgwick and H. M. Powell, Proc. Roy. Soc. A176, 153 (1940),
- ↑ R. J. Gillespie and R. S. Nyholm, Quart. Rev. Chem. Soc., 11, 339 (1957).
- ↑ R. J. Gillespie, "Fifty years of the VSEPR model," Coord. Chem. Rev. 252, 1315-1327 (2008). DOI: 10.1016/j.ccr.2007.07.007
- ↑ Pauling, L. (1932). "化学键的本质。IV. 单键的能量和原子的相对电负性". J. Am. Chem. Soc. 54 (9): 3570–3582. doi:10.1021/ja01348a011.
- ↑ Mulliken, R. S. (1934). "一个新的电亲和力标度;以及关于价态和价态电离势和电子亲和力的数据". J. Chem. Phys. 2 (11): 782–793. Bibcode:1934JChPh...2..782M. doi:10.1063/1.1749394.
- ↑ Mulliken, R. S. (1935). "分子的电子结构XI. 电亲和力、分子轨道和偶极矩". J. Chem. Phys. 3 (9): 573–585. Bibcode:1935JChPh...3..573M. doi:10.1063/1.1749731.
- ↑ Pearson, R. G. (1985). "路易斯酸和碱的绝对电负性和绝对硬度". J. Am. Chem. Soc. 107 (24): 6801. doi:10.1021/ja00310a009.
- ↑ B. Hammer and J. K. Norskov, "为什么金是所有金属中最惰性的", 自然 376, 238 - 240 (2002. doi:10.1038/376238a0
- ↑ Schomaker, Verner; Stevenson, D. P. (1941). "共价半径的一些修正和部分离子单共价键长度的加和规则 *". 美国化学会志. 63: 37–40. doi:10.1021/ja01846a007.
- ↑ Pauling, L. 化学键的本质,第 3 版;康奈尔大学出版社:纽约伊萨卡,1960 年;第 224 页。
- ↑ Robinson, Edward A.; Johnson, Samuel A.; Tang, Ting-Hua; Gillespie, Ronald J. (1997). "用几乎离子模型重新解释与氟的键长". 无机化学. 36 (14): 3022–3030. doi:10.1021/ic961315b. PMID 11669953.
- ↑ Pyykkö, Pekka; Atsumi, Michiko (2009). "元素 Li–E112 的分子双键共价半径". 化学:欧洲期刊. 15 (46): 12770–12779. doi:10.1002/chem.200901472.
- ↑ V. H. Dalvi and P. J. Rossky, 氟碳疏水性的分子起源,美国国家科学院院刊 107,13603–13607 (2010). DOI: 10.1073/pnas.0915169107.


































![{\displaystyle \chi _{\rm {A}}-\chi _{\rm {B}}={\sqrt {E_{\rm {d}}({\rm {AB}})-[E_{\rm {d}}({\rm {AA}})+E_{\rm {d}}({\rm {BB}})]/2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93475ab1444be44f5df567732672dcef9630e8b3)






