数学物理导论/量子力学中的N体问题/分子

弹簧模型的振动

我们这里处理一个简单的分子模型\index{molecule}来强调使用\index{symmetry}在分子研究中的重要性。 水分子 H$_{2}$0 属于称为 $C_{2v}$ 的点群。该群由四个对称操作组成：恒等操作 $E$，旋转 $C_{2}$ 角度为 $\pi$，以及两个平面对称性 $\sigma _{v}$ 和 $\sigma '_{v}$ 相对于通过 $C_{2}$ 操作旋转轴的两个平面（见图 figmoleceau）。

figmoleceau

水分子。 对称群 $C_{2v}$ 对应于一组操作：恒等操作 $E$，旋转 $C_{2}$ 角度为 $\pi$ 绕垂直轴，对称性 $\sigma _{v}$ 相对于垂直于纸张的平面，以及对称性 $\sigma '_{v}$ 相对于纸张的平面。

群 $C_{2v}$ 是 32 个可能的点群之一 ([ma:group:Jones90][ph:solid:Ashcroft76])。 命名法在图 ---figsymetr--- 中解释。

figsymetr

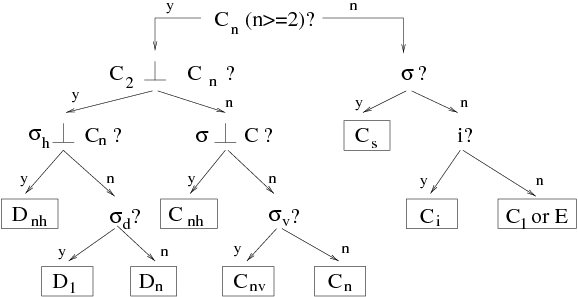化学对称群的命名法。从树的顶部开始依次测试对称操作的出现。根据问题的答案，通过树进行遍历，“o”表示是，“n”表示否。$C_{n}$ 表示旋转角度为 $2\pi /n$，$\sigma _{h}$ 表示关于水平平面（垂直于$C_{n}$ 轴）的对称操作，$\sigma _{h}$ 表示关于垂直平面（经过$C_{n}$ 轴）的对称操作，而$i$ 表示反演。群的名称用框框起来。

这些群中的每一个都可以用“特征”表来描述，这些特征表定义了这个群的可能不可约表示\index{不可约表示}。群$C_{2v}$ 的特征表是

tabchar

群$C_{2v}$ 的特征群。

$C_{2v}$	$E$	$C_{2}$	$\sigma _{v}$	$\sigma '_{v}$
$A_{1}$	1	1	1	1
$A_{2}$	1	1	-1	-1
$B_{1}$	1	-1	1	-1
$B_{2}$	1	-1	-1	1

群 $C_{2v}$ 的所有表示都是一维的。有四个表示，分别标记为 $A_{1}$，$A_{2}$，$B_{1}$ 和 $B_{2}$。在水分子情况下，九维空间中的 $e_{i}$ $i=1,\dots ,9$。实际上，每个原子由三个坐标表示。表示在这里对应于选择向量 $e_{i}$ 的一个线性组合 $u$，使得对于对称群 $g$ 的每个元素，都有

$g(u)=M_{g}u.$

特征表提供了每个运算 $g$ 的表示矩阵 $M_{g}$ 的迹。由于这里考虑的所有表示都是一维的，特征只是 $M_{g}$ 的（唯一）特征值。图 figmodesmol 绘制了水分子 $C_{2v}$ 群的九个表示。可以看出，由向量 $e_{i}$ 张成的空间可以被分成九个由运算 $g$ 不变的子空间。引入表示和 ([ma:group:Jones90])，所考虑的表示 $D$ 可以写成不可约表示的和

$D=3A_{1}\oplus A_{2}\oplus 2B_{1}\oplus 3B_{2}.$

figmodesmol

---

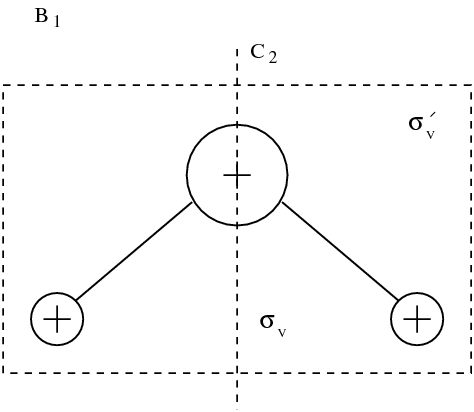
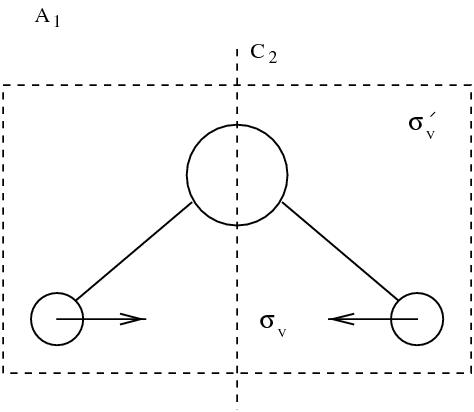
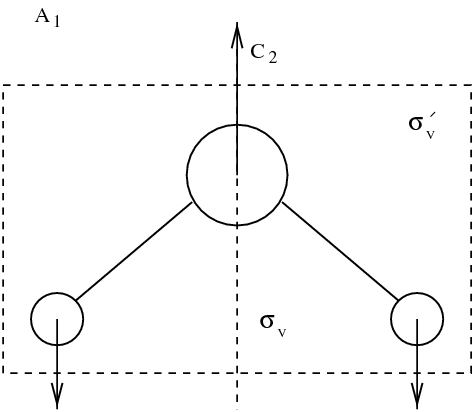
$H_{2}O$ 分子的本征模态。振动模态用方框框起来。其他模态对应于旋转和平移。

---

在九种模态中，有三种平移模态和三种旋转模态。这些模态保持分子原子间距离不变。图figmodesmol中用方框框起来的是三种真实的振动模态。动力学通常由

${\frac {d^{2}x}{dt^{2}}}=Mx$

定义，其中$x$ 是在$e_{i}$ 基下定义系统状态的向量。然后在对应于三种振动模态的坐标系中对动力学进行对角化。这里，对称性考虑足以获得特征向量。一旦$M$ 的系数的数值已知，就可以快速地计算出特征值。

两个原子核，一个电子

这种情况对应于H$_{2}^{+}$ 分子的研究（[#References|参考文献]）。我们在这里使用的玻恩-奥本海默近似假设质子是固定不动的（质子的运动相对于电子的运动很慢）。

注：这个问题可以精确求解。然而，我们在这里介绍的变分近似可以用于更复杂的情况。

我们在这里介绍的 LCAO（原子轨道线性组合）方法是变分方法的一个特例。它通过原子的一电子波函数的线性组合来逼近电子波函数[注：即解空间被原子波函数所张成的子空间近似].

$\psi =a\psi _{1}+b\psi _{2}$

更准确地说，让我们选择$\phi _{s,1}$ 和 $\phi _{s,2}$ 作为基函数，它们分别是分别以原子$1$ 和 $2$ 为中心的$s$ 轨道。这种近似随着 R 的增大而变得更加有效（参见图figH2plusS）。

H$_{2}^{+}$ 分子： 选择与每个氢原子相关的$1s$ 函数作为变分方法中使用的基函数。

figH2plusS

问题的对称性导致将特征向量写成

${\begin{matrix}\psi _{g}&=&N_{g}(\psi _{1}+\psi _{2})\\\psi _{u}&=&N_{u}(\psi _{1}-\psi _{2})\end{matrix}}$

使用指标符号 $g$ 和 $u$，回想起函数的奇偶性：$g$ 代表德语中的 "gerade"，即偶数，而 $u$ 代表德语中的 "ungerade"，即奇数。图 figH2plusLCAO 表示这两个函数。

函数 $\psi _{g}$ 和 $\psi _{u}$ 是基于两个氢原子 $s$ 轨道进行变分近似问题求解得到的解。

figH2plusLCAO

考虑到哈密顿量，可以使能量简并，如图 figH2plusLCAOener 的图示所示。

使用氢原子 $s$ 轨道作为基底，用 LCAO 方法推导出的 $H_{2}^{+}$ 分子的能量图。

figH2plusLCAOener

secnnne

N 个原子核，n 个电子

在这种情况下，对称性的考虑有助于找到简化谱问题的特征子空间。这些考虑与点群表示论有关。当同一分子的原子位于平面上时，该平面就是一个对称元素。对于线性分子，任何沿着这条直线经过的平面也是对称平面。可以区分两种类型的轨道。

定义

轨道 $\sigma$ 在关于对称平面的反射中保持不变。

定义： 轨道 $\pi$ 在关于该平面的反射中改变符号。

让我们考虑一个线性分子。其他例子，请参考 ([#References|参考资料])。

例子: 分子 BeH$_{2}$。我们寻找一个在由轨道 $2s$ 和 $z$ 跨越的空间中的波函数，铍原子 Be 的 $2s$ 和 $z$，以及两个氢原子的两个轨道 $1s$。因此空间是四维的（轨道 $x$ 和 $y$ 未被使用），在这个基底上对角化的哈密顿量通常被写成一个 $4\times 4$ 矩阵。考虑到所考虑分子的对称性，该矩阵可以写成一个 *块对角矩阵*。让我们选择以下基底作为状态空间的近似：\{$2s,z,1s_{1}+1s_{2},1s_{1}-1s_{2}$\}. 然后对称性考虑表明轨道必须是

${\begin{matrix}\sigma _{s}&=&\alpha _{1}2s+\beta _{1}(1s_{1}+1s_{2})\\\sigma _{s}^{*}&=&\alpha _{2}2s-\beta _{2}(1s_{1}+1s_{2})\\\sigma _{p}&=&\alpha _{3}z+\beta _{3}(1s_{1}-1s_{2})\\\sigma _{p}^{*}&=&\alpha _{4}z-\beta _{4}(1s_{1}-1s_{2})\end{matrix}}$

这些键在三个原子之间是离域的，并在图 figBeH2orb 中进行了描绘。

使用 LCAO 方法研究 $H_{2}^{+}$ 分子。选择的基底是氢原子的两个轨道 $s$。}

figBeH2orb

我们有两个成键轨道和两个反键轨道。能级图在图 figBeH2ene 中表示。在基态，四个电子占据两个成键轨道。

使用 LCAO 方法绘制 $H_{2}^{+}$ 分子的能级图。选择的基底是氢原子的两个轨道 $s$。}

figBeH2ene

对分子的实验研究表明，键的特性仅略微依赖于其他原子的性质。因此，问题被简化为考虑 $\sigma$ 分子轨道是双中心的，这意味着它位于两个原子之间。这些轨道被称为杂化轨道。

示例： 让我们再次以 BeH$_{2}$ 分子为例。该分子是线性的。这种几何形状可以通过 $s-p$ 杂化来很好地描述。

${\begin{matrix}d_{1}&=&{\frac {1}{\sqrt {2}}}(s+z)\\d_{2}&=&{\frac {1}{\sqrt {2}}}(s-z)\end{matrix}}$

与其考虑基底 {$2s,z,1s_{1},1s_{2}$\}，不如直接考虑基底 {$d_{1},d_{2},1s_{1},1s_{2}$\}。因此，从一开始，光谱问题就得到了很好的解决。