数值方法导论/插值

目标

• 理解插值
• 推导牛顿插值公式
• 推导拉格朗日插值公式
• 应用插值方法解决问题
• 使用插值找到离散函数的导数和积分

资源

• 直接法章节
• 牛顿法章节
• 拉格朗日法章节
• 样条法章节
• 插值的编年史
• NIST 数字数学函数库

插值

插值 是从一组离散数据点中推导出一个简单函数的过程，使该函数通过所有给定的数据点（即精确地再现数据点），并可用于估计给定数据点之间的其他数据点。 这是必要的，因为在科学和工程中，我们经常需要处理离散的实验数据。 插值还用于通过对数据点进行采样并使用更简单的函数对其进行插值来简化复杂的函数。 多项式通常用于插值，因为它们更容易计算、微分和积分 - 称为 多项式插值。

可以证明，给定 n+1 个数据点，总能找到一个 n 阶/度多项式来通过/再现这 n+1 个点。

直接法

给定 n+1 个数据点，直接法假设以下多项式

$y=f(x)=a_{0}+a_{1}x+a_{2}x^{2}+...+a_{n}x^{n}$

对于 $x$ 的 n+1 个值和相应的 $y$ 的 n+1 个值，我们可以通过解 n+1 个联立线性方程组来求解 $a_{0},a_{1},...,a_{n}$，这被称为直接法。

例如，给定两个数据点 $(x_{0},y_{0})$ 和 $(x_{1},y_{1})$，我们可以使用线性函数 $y=f(x)=a_{0}+a_{1}x$ 来通过这两个数据点

$y_{0}=a_{0}+a_{1}x_{0}$

$y_{1}=a_{0}+a_{1}x_{1}$

一旦我们求解了 $a_{0}$ 和 $a_{1}$（$f(x)$ 的系数），我们可以使用该函数作为插值的依据——估计其间的缺失数据点。

牛顿法

在牛顿法中，插值函数以 牛顿多项式（又称牛顿形式）的形式写出。例如，给定一个数据点 $(x_{0},y_{0})$，我们只能推导出一个零阶多项式： $y=f(x)=a_{0}$。因为 $f(x_{0})=y_{0}$，零阶牛顿多项式为 $y=f(x)=y_{0}$。

给定两个数据点，我们可以将牛顿多项式写成 $y=f(x)=a_{0}+a_{1}(x-x_{0})$ 的形式。将两个数据点代入，得到

$a_{0}=y_{0}$

$a_{1}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$

显然，该函数通过这两个数据点（即准确地再现了这两个数据点）。该函数在 $x=x_{0}$ 处的导数为 $f'(x_{0})=a_{1}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$，与前向差分法的结果一致。

给定三个数据点，我们可以将牛顿多项式写成

$y=f(x)=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{1})(x-x_{0})$

将三个数据点代入，得到

由于 $y_{0}=a_{0}$，我们得到 $a_{0}=y_{0}$

由于 $y_{1}=a_{0}+a_{1}(x_{1}-x_{0})$，我们得到 $a_{1}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$

由于 $y_{2}=a_{0}+a_{1}(x_{2}-x_{0})+a_{2}(x_{2}-x_{1})(x_{2}-x_{0})$

我们得到

${\begin{aligned}a_{2}&={\frac {y_{2}-a_{0}-a_{1}(x_{2}-x_{0})}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {y_{2}-y_{0}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x_{2}-x_{0})}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {y_{2}-y_{0}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}((x_{2}-x_{1})+(x_{1}-x_{0}))}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {y_{2}-y_{0}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x_{2}-x_{1})-(y_{1}-y_{0})}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {y_{2}-y_{1}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x_{2}-x_{1})}{(x_{2}-x_{1})(x_{2}-x_{0})}}\\&={\frac {{\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}-{\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}}{x_{2}-x_{0}}}\\\end{aligned}}$

这个三次多项式函数通过所有三个数据点（二阶导数和三阶导数在 $x_{0}$ 和 $x_{1}$ 处与差商法匹配）。

从这两个例子中，我们可以看到牛顿多项式的系数遵循一种称为 差商 的模式。例如，$a_{1}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}$ 被称为一阶差商（记为 $f[x_{0},x_{1}]$），因为它取决于 $x_{0}$ 和 $x_{1}$。差商符号可以用来写出一般阶（形式）的牛顿多项式

$f(x)=f[x_{0}]+f[x_{0},x_{1}](x-x_{0})+f[x_{0},x_{1},x_{2}](x-x_{0})(x-x_{1})+...$

$+f[x_{0},x_{1},x_{2},...,x_{n}](x-x_{0})(x-x_{1})(x-x_{2})...(x-x_{n-1})$

其中

$a_{0}=f[x_{0}]=y_{0}$，因为根据定义 $f[x_{i}]=y_{i}$

$a_{1}=f[x_{0},x_{1}]={\frac {f[x_{1}]-f[x_{0}]}{x_{1}-x_{0}}}$

$a_{2}=f[x_{0},x_{1},x_{2}]={\frac {f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}}$

$\dots$

$a_{k}=f[x_{0},x_{1},x_{2},\dots ,x_{k-1},x_{k}]={\frac {f[x_{1},x_{2},\dots ,x_{k-1},x_{k}]-f[x_{0},x_{1},x_{2},\dots ,x_{k-1}]}{x_{k}-x_{0}}}$

我们可以使用以下表格计算牛顿多项式的系数。

${\begin{matrix}x_{0}&y_{0}=f[x_{0}]&&&\\&&f[x_{0},x_{1}]&&\\x_{1}&y_{1}=f[x_{1}]&&f[x_{0},x_{1},x_{2}]&\\&&f[x_{1},x_{2}]&&f[x_{0},x_{1},x_{2},x_{3}]\\x_{2}&y_{2}=f[x_{2}]&&f[x_{1},x_{2},x_{3}]&\\&&f[x_{2},x_{3}]&&\\x_{3}&y_{3}=f[x_{3}]&&&\\\end{matrix}}$

因为

$f[x_{i}]=y_{i}$

$f[x_{i},x_{i+1}]={\frac {f[x_{i+1}]-f[x_{i}]}{x_{i+1}-x_{i}}}$

下图展示了差商之间的依赖关系。

例如，给定数据点 $(1,6)$, $(2,11)$, $(3,18)$, 以及 $(4,27)$，我们可以绘制以下表格。

${\begin{array}{|c||c|c|c|c|c|}i&x_{i}&y_{i}&f[x_{i},x_{i+1}]&f[x_{i},x_{i+1},x_{i+2}]&f[x_{i},x_{i+1},x_{i+2},x_{i+3}]\\\hline 0&x_{0}=1&{\begin{aligned}y_{0}&=f[x_{0}]\\&=6\end{aligned}}&{\begin{aligned}f[x_{0},x_{1}]&={\frac {f[x_{1}]-f[x_{0}]}{x_{1}-x_{0}}}\\&={\frac {11-6}{2-1}}\\&=5\end{aligned}}&{\begin{aligned}f[x_{0},x_{1},x_{2}]&={\frac {f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}}\\&={\frac {7-5}{3-1}}\\&=1\end{aligned}}&{\begin{aligned}&f[x_{0},x_{1},x_{2},x_{3}]\\&={\frac {f[x_{1},x_{2},x_{3}]-f[x_{0},x_{1},x_{2}]}{x_{3}-x_{0}}}\\&={\frac {1-1}{4-1}}\\&=0\end{aligned}}\\\hline 1&x_{1}=2&{\begin{aligned}y_{1}&=f[x_{1}]\\&=11\end{aligned}}&{\begin{aligned}f[x_{1},x_{2}]&={\frac {f[x_{2}]-f[x_{1}]}{x_{2}-x_{1}}}\\&={\frac {18-11}{3-2}}\\&=7\end{aligned}}&{\begin{aligned}f[x_{1},x_{2},x_{3}]&={\frac {f[x_{2},x_{3}]-f[x_{1},x_{2}]}{x_{3}-x_{1}}}\\&={\frac {9-7}{4-2}}\\&=1\end{aligned}}&\\\hline 2&x_{2}=3&{\begin{aligned}y_{2}&=f[x_{2}]\\&=18\end{aligned}}&{\begin{aligned}f[x_{2},x_{3}]&={\frac {f[x_{3}]-f[x_{2}]}{x_{3}-x_{2}}}\\&={\frac {27-18}{4-3}}\\&=9\end{aligned}}&&\\\hline 3&x_{3}=4&{\begin{aligned}y_{3}&=f[x_{3}]\\&=27\end{aligned}}&&&\\\end{array}}$

四个数据点位于一个二阶多项式上，这就是系数 $a_{3}$($f[x_{0},x_{1},x_{2},x_{3}]$) 为零。给定 $[a_{0},a_{1},a_{2}]=[6,5,1]$，结果多项式为

${\begin{aligned}y&=a_{0}+a_{1}(x-x_{0})+a_{2}(x-x_{1})(x-x_{0})\\&=6+5\times (x-1)+1\times (x-2)(x-1)\\&=x^{2}+2x+3\end{aligned}}$

求解牛顿多项式的系数后，我们可以对任何 $x$ 求解多项式函数。牛顿多项式通常被重写成嵌套形式

$f(x)=a_{0}+(x-x_{0})(a_{1}+(x-x_{1})(a_{2}+(x-x_{2})(a_{3}+...+a_{n}(x-x_{n-1}))...)$,

因为这种插值多项式的嵌套形式更容易计算，因为 x 只在函数中出现 n 次。

例如，三阶插值多项式的嵌套形式为

$f(x)=a_{0}+(x-x_{0})(a_{1}+(x-x_{1})(a_{2}+(x-x_{2})a_{3}))$

牛顿法的算法及其实现可以在这个 Jupyter notebook 中找到。

拉格朗日形式

拉格朗日多项式 是另一种用于多项式插值的表达式。它被称为一种表达式，因为对于一组给定的不同点，插值多项式是唯一的。我们可以通过不同的方法得到相同的多项式。

拉格朗日表达式将插值多项式指定为

$f_{n}(x):=\sum _{i=0}^{n}L_{i}(x)f(x_{i})$

$L_{i}(x):=\prod _{\begin{smallmatrix}0\leq m\leq n\\m\neq i\end{smallmatrix}}{\frac {x-x_{m}}{x_{i}-x_{m}}}={\frac {(x-x_{0})}{(x_{i}-x_{0})}}\cdots {\frac {(x-x_{i-1})}{(x_{i}-x_{i-1})}}{\frac {(x-x_{i+1})}{(x_{i}-x_{i+1})}}\cdots {\frac {(x-x_{n})}{(x_{i}-x_{n})}},$

其中 $n$ 是多项式的阶数。

例如，给定两个数据点，我们得到 $n=1$ 并且

${\begin{aligned}f(x)&=L_{0}f(x_{0})+L_{1}f(x_{1})\\&={\frac {x-x_{1}}{x_{0}-x_{1}}}f(x_{0})+{\frac {x-x_{0}}{x_{1}-x_{0}}}f(x_{1})\\\end{aligned}}$

显然，函数曲线经过两个数据点。一阶导数也与差商法的一阶导数一致

${\begin{aligned}f'(x)&={\frac {f(x_{0})}{x_{0}-x_{1}}}+{\frac {f(x_{1})}{x_{1}-x_{0}}}\\&={\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}\\\end{aligned}}$

样条插值

样条插值 使用多个多项式函数来插值一组数据点，每个多项式对应两个相邻数据点。样条法是必要的，因为当多项式的阶数变大时，多项式插值往往会表现出振荡行为（称为 龙格现象）。以下 iPython 笔记本展示了一个遇到此问题的例子：[1]

样条法不是另一种寻找离散函数的多项式插值的方法，而是使用分段多项式（样条）来避免振荡行为。最常见的样条插值是线性样条、二次样条和三次样条。 线性插值 使用直线连接每对连续数据点，从而形成分段插值。

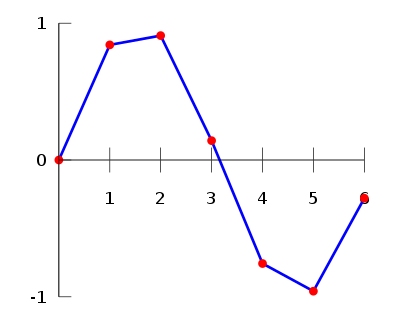
一个 二次样条 使用二次多项式连接连续数据点。

如果满足以下条件，则函数 f(x) 是一个二次样条

1. f(x) 的定义域为区间 [a, b]。
2. $f(x)$ 和 $f'(x)$ 在 [a, b] 上是连续的。
3. 数据点 $x_{i}$ 使得 $a=x_{0}<x_{1}<\dots <x_{n}=b$ 并且 $f(x)$ 在每个子区间 $[x_{i},x_{i+1}]$ 上最多是 2 阶多项式。