JPEG - 思想与实践/霍夫曼编码
我们与真实JPEG程序的区别在于,在第一部分中,我们使用了易于理解和使用的编码方法,但效率不高,部分原因是它基于频率,这些频率更多地由我们对简单编码程序的渴望决定,而不是现实。JPEG使用更高效的霍夫曼编码和频率,这些频率要么由实际图像决定,要么由许多典型图像的平均值决定。此外,我们对所有数字使用相同的编码程序,而JPEG对直流和交流数字使用不同的编码,并且对Y分量和两个颜色分量也使用不同的编码 - 这意味着编码可能需要超过450个数字的表。
在这里,我们将选择基于典型频率的霍夫曼表,而不是基于对实际图像进行预扫描测量的频率。因此,我们只需要知道一旦我们有了必要的表格,如何执行霍夫曼编码和解码:我们不需要知道这些表格是如何根据频率构建的。但是,我们将展示构建霍夫曼表的程序。这是一个相当简单的程序,读者可能想要编写一个程序来测量频率并从实际图像构建霍夫曼表(我们将在附录2中展示程序)。
假设我们有一些值a1,a2,…,an,这些值附加有频率,并且需要用代码字来表示,以便最常用的值获得最短的代码。这可以通过构建一个所谓的霍夫曼树来实现,该树以值作为叶子,并附有频率。通常,霍夫曼树可以用多种方式构建,从而产生不同的代码长度。JPEG选择以下方法
我们按频率递减的顺序排列这些值。对于最后两个值,我们添加它们的频率,删除这两个值,并在剩余值中的适当位置插入一个节点(以便频率仍然递减 - 注意,如果新频率出现在其他值中,则可以在多个位置插入)。重复此操作,直到只剩下一个节点,该节点的频率为1。对于每个操作,我们都删除了两样东西:要么两个值,要么两个节点,要么一个值和一个节点。我们通过将值(叶子)放在底部,并依次用线连接被删除的两样东西及其替代节点来构建霍夫曼树。
例如,如果值是数字0,1,2,3和4,并且它们的频率分别是0.3,0.25,0.2,0.15和0.1(总和为1),则删除过程可能如下所示
- a1 0 0.3 0.3 0.45 0.55 1
- a2 1 0.25 0.25 0.3 0.45
- a3 2 0.2 0.25 0.25
- a4 3 0.15 0.2
- a5 4 0.1
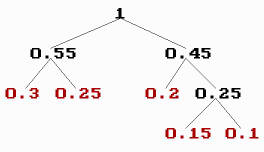
霍夫曼树可能如下所示
分配给某个值的霍夫曼代码的长度是从该值到最后一个节点(频率为1的顶部节点)的线数。一旦我们知道了分配给这些值的长度(代码),我们就可以形成代码字,并且可以通过多种方式完成这项工作
通过使用霍夫曼树,我们可以编码,例如,当我们从值向顶部节点前进时,向右走写1,向左走写0
- 0 00
- 1 10
- 2 01
- 3 011
- 4 111
但我们也可以在没有霍夫曼树的情况下进行编码,重要的是分配给值的代码长度。例如,我们可以编码,使代码字的序列(通过它们的二进制数字表达式识别)递增:当代码长度不变时形成连续数字,并且当代码长度增加时附加零
- 0 00
- 1 01
- 2 10
- 3 110
- 4 111
JPEG使用这种最后一种形成代码的方法,因为它解码速度很快。
在JPEG中,代码字不能只由1组成。我们可以通过临时添加一个额外的值来避免这种情况,该值的频率是最后一个小值频率的一半(例如),最后从最大长度的代码中删除一个代码。
此外,代码字的长度不能超过16。因此,如果霍夫曼树导致代码长度超过16位,则必须依次缩短最长的代码。在我们导入编码的情况下,我们不需要关心这个问题,但我们将简要描述它:最长的代码长度分配给偶数个值。因此,我们可以将最长长度缩短一位(最后一位),并将此代码分配给其中一个值,如果我们能找到另一个(更短的)代码给另一个值。假设最后(最长)代码有j位,我们可以删除这些代码中的最后一个(长度为j),并将它分别扩展为0和1,以便我们获得两个新的长度为j+1的代码,它们可以替换两个被删除的代码。
霍夫曼编码是根据(霍夫曼)值(出现在图像中)和分配给每个值的代码长度(由其频率决定)执行的。因此,我们的出发点是两个字节列表:第一个称为BITS,从1到16,它告诉我们,对于这些数字中的每一个,此代码长度的代码数量。第二个称为HUFFVAL,它为每个代码长度(具有非零代码数量)按顺序列出要使用此长度代码编码的值(以及与该长度代码数量相同的数量的值)。HUFFVAL中的值称为霍夫曼值,它们按递增代码长度的顺序排列(在给定的代码长度内,排序是任意的)。
在我们的程序中,我们使用这些列表来表示Y分量的直流数字
- BITS
- 0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0
- HUFFVAL
- 0
- 1 2 3 4 5
- 6
- 7
- 8
- 9
- 10
- 11
以及这些列表来表示两个颜色分量的直流数字
- BITS
- 0 3 1 1 1 1 1 1 1 1 1 0 0 0 0 0
- HUFFVAL
- 0 1 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
最后这些列表表明,存在:长度为1的0个代码,长度为2的3个代码(编码霍夫曼值0、1和2),长度为3的1个代码(编码霍夫曼值3),等等。
大多数要编码的数字是交流数字,它们与直流数字的编码方式不同。此外,这些值的范围更大。由于我们引入了霍夫曼编码,我们必须使用包含所有可能值的列表。
在我们的程序中,我们使用这些列表来表示Y分量的交流数字
- BITS
- 0 2 1 3 3 2 4 3 5 5 4 4 0 0 1 125
- HUFFVAL
- 1 2
- 3
- 0 4 17
- 5 18 33
- 49 65
- 6 19 81 97
- 7 34 113
- 20 50 129 145 161
- 8 35 66 177 193
- 21 82 209 240
- 36 51 98 114
- 130
- 9 10 22 23 24 25 26 37 38 39 40 41 42 52 53 54 55 56 57 58 67 68 69 70 71 72 73 74 83 84 85 86 87 88 89 90 99 100 101 102 103 104 105 106 115 116 117 118 119 120 121 122 131 132 133 134 135 136 137 138 146 147 148 149 150 151 152 153 154 162 163 164 165 166 167 168 169 170 178 179 180 181 182 183 184 185 186 194 195 196 197 198 199 200 201 202 210 211 212 213 214 215 216 217 218 225 226 227 228 229 230 231 232 233 234 241 242 243 244 245 246 247 248 249 250
以及这些列表来表示两个颜色分量的交流数字
- BITS
- 0 2 1 2 4 4 3 4 7 5 4 4 0 1 2 119
- HUFFVAL
- 0 1
- 2
- 3 17
- 4 5 33 49
- 6 18 65 81
- 7 97 113
- 19 34 50 129
- 8 20 66 145 161 177 193
- 9 35 51 82 240
- 21 98 114 209
- 10 22 36 52
- 225
- 37 241
- 23 24 25 26 38 39 40 41 42 53 54 55 56 57 58 67 68 69 70 71 72 73 74 83 84 85 86 87 88 89 90 99 100 101 102 103 104 105 106 115 116 117 118 119 120 121 122 130 131 132 133 134 135 136 137 138 146 147 148 149 150 151 152 153 154 162 163 164 165 166 167 168 169 170 178 179 180 181 182 183 184 185 186 194 195 196 197 198 199 200 201 202 210 211 212 213 214 215 216 217 218 226 227 228 229 230 231 232 233 234 242 243 244 245 246 247 248 249 250
如果我们把霍夫曼值的个数称为nhv,那么我们就有一个数组HUFFVAL[k],从k = 1到nhv,它按枚举顺序排列霍夫曼值。从列表BITS[i],我们形成一个数组HUFFSIZE[k],从k = 1到nhv,其中包含代码长度i(对于其BITS[i]非零的i),每个i重复BITS[i]次,因此数组HUFFSIZE[k]与HUFFVAL[k]平行。现在我们构建一个数组HUFFCODE[k],从k = 1到nhv,它指出分配给HUFFVAL[k]的霍夫曼代码。我们将一个代码用具有代码位作为二进制数字表达式的整数来识别(例如110 = 6),注意,由于代码可能以一个或多个零开头,因此数字表达式必须以零开头才能得到正确的长度(例如011 = 3)。
代码字的生成方式如下:假设我们已经形成了所有长度<= n的代码,并且最后一个形成的代码是数字c。现在假设下一个代码长度是n+i,那么下一个代码是c = 2i∙(c + 1)(通过将i个零连接到c + 1而得到的代码),接下来的代码是连续数字(c+1,c+2,…),数量与(新)长度n = n+i的代码数量相同。在开始时,c设置为0。代码编号k,HUFFCODE[k],是分配给霍夫曼值HUFFVAL[k]的代码。
为了编码,我们重新排列列表(数组)HUFFSIZE和HUFFCODE,使它们成为霍夫曼值的函数(而不是顺序号的函数),形成数组EHUFSI[val]和EHUFCO[val]
- 如果val = HUFFVAL[k],那么
- EHUFSI[val] = HUFFSIZE[k],并且
- EHUFCO[val] = HUFFCODE[k]
- 如果val = HUFFVAL[k],那么
注意,EHUFCO[val]是一个数组:EHUFCO[val][j]是代码的第j位。
如果我们令函数 *size*(n) (n 为整数) 表示 n 的二进制表示中数字的个数,并令 *digit*(n) 为数字表示本身(因此 *digit*(n) 是从 1 到 *size*(n) 的一位数组),那么构造 HUFFSIZE[k]、HUFFCODE[k]、EHUFSI[val] 和 EHUFCO[val] 的过程(这些过程应用于每个霍夫曼表)可以如下所示。
- k = 1
- i = 1
- j = 1
1
- 如果 j <= bits[i] 则
- 开始
- huffsize[k] = i
- k = k + 1
- j = j + 1
- 转到 1
- 结束
- 开始
- i = i + 1
- j = 1
- 如果 i <= 16 则
- 转到 1
- nhv = k - 1
- k = 1
- c = 0
- i = huffsize[k]
2
- huffcode[k] = c
- c = c + 1
- 如果 k = nhv 则
- 转到 4
- k = k + 1
- 如果 huffsize[k] = i 则
- 转到 2
3
- c = 2 * c
- i = i + 1
- 如果 huffsize[k] = i 则
- 转到 2
- 否则
- 转到 3
4
- k = 1
5
- val = huffval[k]
- e = huffsize[k]
- ehufsi[val] = e
- l = size(huffcode[k])
- dig = digit(huffcode[k])
- 如果 l < e 则
- 对于 j 从 1 到 e - l 做
- ehufco[val, j] = 0
- 对于 j 从 1 到 e - l 做
- 对于 j 从 1 到 l 做
- ehufco[val, e - l + j] = dig[j]
- k = k + 1
- 如果 k <= nhv 则
- 转到 5
对于上面的 Y 分量的 DC 数字列表,nhv = 12,HUFFSIZE[k] 是序列 2 3 3 3 3 3 4 5 6 7 8 9,HUFFCODE[k] 是序列 00, 010, 011, 100, 101, 110, 1110, 11100, 111000, 1110000, 11100000, 111000000。对于函数 EHUFSI[val] 和 EHUFCO[val],我们有:EHUFSI[0] = 2, EHUFSI[1] = 3, EHUFSI[2] = 3,等等,以及 EHUFCO[0] = 00, EHUFCO[1] = 010, EHUFCO[2] = 011,等等。
在编码中,对于非负整数 n,我们必须知道 n 的二进制表示中包含多少位数字。函数 *size*(n) 表示这个数字,它扩展到负数 n,让 -n 与 n 有相同的位数。它由 *size*(0) = 0 和 *size*(n) = trunc(ln(abs(n)) / ln(2) + 0.000001) + 1 当 n != 0 时给出。
- n size
- 0 0
- 1 1
- 2, 3 2
- 4 ... 7 3
- 8 ... 15 4
- 16 ... 31 5
- 32 ... 63 6
- 64 .. 127 7
- 128 .. 255 8
- 256 .. 511 9
- 512 .. 1023 10
- 1024 .. 2047 11
- 等等。
二进制表示遵循霍夫曼代码的整数可以为负数,并且(如 *第一部分* 中所解释的)我们不需要额外的位来表示这一点:数字表示始终以 1 开头,我们可以用 0 代替 1。在解码序列时,以 0 开头将表明该数字为负数,而 1 后面跟着其余数字将是数值的二进制表示。但是,为了表明该数字为负数,JPEG 选择用其相反的位(形成该数字的 *补码*)替换 *所有* 数字。因此,如果数字表示以 0 开头,具有 val 位并且对应于(非负)整数 n,那么负整数为 -(2val - 1 - n)(在 T.81 中提到,如果数字序列以 0 开头,并且数字个数为 T,那么通过将 2T + 1 加到该数字,我们得到数值,但这不正确,当然,该数字是通过将其从 2T - 1 = 11...1(T 个 1)中减去得到的)。
函数 *digit*(n) (n != 0) 的程序,它给出整数 n 的二进制表示(当 n 为正数时)以及数字表示的补码(当 n 为负数时)可以如下所示。
- j = size(n)
- 如果 n < 0 则
- n = round(exp(j * ln(2))) - 1 - abs(n)
- 如果 j = 1 则
- digit[1] = n
- 否则
- 开始
- j = j - 1
- q = round(exp(j * ln(2)))
- i = 0
- 当 i <= j 时
- 开始
- i = i + 1
- l = n div q
- n = n - l * q
- q = q div 2
- digit[i] = l
- 结束
- 开始
- 结束
- 开始
**DC 数字:** 对于 DC 数字(64 数组中的第一个数字),不是数字本身,而是该数字与前面 DC 数字之间的差值 DIFF 进行编码,并且不是 DIFF 本身,而是表示它所需的位数 val:val = *size*(DIFF)。然后代码为 EHUFCO[val],之后是 DIFF 的 val 个二进制数字:*digit*(DIFF)[j],j = 1,...,val。
**AC 数字:** 63 个 AC 数字(64 数组中的)以与 DC 数字不同的方式编码。这里对实际数字的大小(不是差值)进行编码,并且由于 AC 数组中通常存在很多零,因此连续行中这些零的个数与后面非零 AC 数字的大小 *合并*。如果有 m 个零在非零 AC 数字 n 之前,并且 n 的大小为 k,我们将这两个数字(为半字节)组合成一个字节 val = m*16 + k,并且是这个字节被霍夫曼编码。然而,这假设 m 和 k 确实是半字节(也就是说,<= 15)。k 始终 <= 11,但是连续行中可能存在超过 15 个零,因此,当一行零达到 15 并后面跟着另一个零时,我们必须单独编码这 16 个零:要编码的字节是 val = 15*16 + 0 = 240(称为 ZRL)。如果 63 个 AC 数字中的最后一个为零,则通过写入分配给 val = 0*16 + 0 = 0(称为 EOB,块结束)的霍夫曼代码来表示这一点。在写入霍夫曼代码之后,非零 AC 数字的 k 个二进制数字以与 DC(或更确切地说 DIFF)数字相同的方式写入。频率和代码长度分配给所有这些(霍夫曼)值 val = m*16 + k,这些值以这种方式构造(或至少是图像中出现的那些值)。霍夫曼值(要编码的)的数量最多可以是可能的零的数量(0, 1, ..., 15,即 16)乘以非零 AC 数字的可能大小的数量(即 10),以及除了这个乘积(160)之外,还有两个额外的值 240 和 0。总共 162 个霍夫曼值。由于我们在这里选择导入基于对大量随机图像测试的霍夫曼表,因此我们的 AC 霍夫曼表最多包含 162 个值。
解码
[edit | edit source]对于解码(当读取文件时)(而不是数组 EHUFSI[val] 和 EHUFCO[val]),我们必须事先从 k = 1 到 16 构造三个数组:长度为 k 的最小(第一个)代码,MINCODE[k],长度为 k 的最大(最后一个)代码,MAXCODE[k],以及代码(和霍夫曼值)序列中 MINCODE[k] 的 *数量*,VALPTR[k](值指针)。
- j = 0
- k = 0
0
- k = k + 1
- 如果 k > 16 则
- 转到 fin
- 如果 bits[k] = 0 则
- 开始
- maxcode[k] = -1
- 转到 0
- 结束
- 开始
- j = j + 1
- valptr[k] = j
- mincode[k] = huffcode[j]
- j = j + bits[k] - 1
- maxcode[k] = huffcode[j]
- 转到 0
fin
注意,当没有长度为 k 的代码时,MAXCODE[k] = -1,并且 MINCODE[k] 和 VALPTR[k] 未定义。
解码如下进行:在位流中,要做的第一件事是收集尽可能多的位,使它们形成一个代码:我们必须确定在哪里停止。我们从 k = 0,c = 0 和 MAXCODE[0] = -1(因此 c > MAXCODE[0])开始,并且对于每个读取的位,我们将它加入 c 并将 k 增加 1,直到 c <= MAXCODE[k]。由于我们将代码与数字标识,因此连接意味着我们将 c 设置为 2*c + bit,对于每个新位(称为 bit)。然后代码为 c,我们将找到分配给 c 的霍夫曼值 val,这是具有数字 k = VALPTR[k] + c - MINCODE[k] 的霍夫曼值,因此 val = HUFFVAL[k]
- k = 0
- c = 0
- 当 c > maxcode[k] 时
- 开始
- nbit
- c = 2 * c + bit
- k = k + 1
- 结束
- 开始
- val = huffval[valptr[k] + c - mincode[k]]
这里 *nbit* 是稍后描述的过程,它读取下一个位。