计算机科学逻辑/命题逻辑

命题逻辑

命题逻辑是介绍逻辑基本性质的一个很好的工具。它不提供确定原子语句的有效性（真或假）的方法。相反，它允许你在给定其原子成分的有效性的情况下评估复合语句的有效性。

例如，考虑以下情况

我喜欢帕特或者我喜欢乔。

如果我喜欢帕特，那么我喜欢乔。

我喜欢乔吗？

接受前两个陈述作为事实，注意这里“或”的使用不是排他的，因此实际上可以认为是在说“我喜欢帕特，或者我喜欢乔，或者我两者都喜欢”。这些陈述是否意味着“我喜欢乔”为真？试着说服自己“我喜欢乔”为真，并考虑另一条推理途径

猪会飞或者鱼会唱歌。

如果猪会飞，那么鱼会唱歌。

鱼会唱歌吗？

我们可以看到，在这两种情况下答案都是是。以上两组陈述都可以抽象如下

${\begin{aligned}&P\lor Q\\&P\to Q\\&Q\end{aligned}}$?

在这里，我们关注的是逻辑推理本身，而不是陈述。因此，我们不使用猪或帕特，而是简单地写$Q$s或$P$s。我们首先从命题逻辑的语法开始我们的研究：也就是说，我们描述逻辑语言中的元素以及它们是如何书写的。然后我们描述这些符号的语义：即符号的含义。

语法

命题逻辑的语法由命题符号、逻辑连接词和括号组成。规则规定了这些元素如何组合在一起。首先，我们将命题符号仅仅视为一些符号的集合，出于我们的目的，我们将使用罗马和希腊字母，并将所有符号的集合称为${\text{Prop}}$

命题符号：一些符号的集合${\text{Prop}}$。例如$p,q,r,\ldots$

其次，我们有逻辑连接词

逻辑连接词：$\land ,\lor ,\neg ,\to$

请注意，这些不是最小的必需集合；它们可以使用单个连接词NOR（非或）或NAND（非与）等效地表示，这些连接词在计算机硬件的最低级别使用。最后，我们使用括号来表示表达式（稍后我们将使括号可选）

括号：$(,)$

表达式是命题符号、括号和逻辑连接词的字符串。

我们考虑的表达式称为公式。公式集${\textrm {Form}}$是最小的表达式集，满足

1. ${\text{Prop}}\subseteq {\text{Form}}$
2. 如果$\phi ,\psi \in {\text{Form}}$，则
   1. $(\phi \land \psi )\in {\text{Form}}$ ,
   2. $(\phi \lor \psi )\in {\text{Form}}$ ,
   3. 若 $(\phi \to \psi )\in {\text{Form}}$，并且
   4. $(\neg \phi )\in {\text{Form}}$ .

另一种定义公式的方法是将其视为由以下上下文无关文法定义的语言（起始符号为 ${\text{Form}}$）

${\text{Form}}\Rightarrow {\text{Prop}}$，其中 ${\text{Prop}}$ 代表任何命题符号

${\begin{aligned}{\text{Form}}\Rightarrow ({\text{Form}}\land {\text{Form}})\\{\text{Form}}\Rightarrow ({\text{Form}}\lor {\text{Form}})\\{\text{Form}}\Rightarrow ({\text{Form}}\to {\text{Form}})\\{\text{Form}}\Rightarrow (\neg {\text{Form}})\end{aligned}}$

事实 1（唯一可读性）：上述上下文无关文法是无歧义的。

语义

公式的功能是在给定原子语句的含义的情况下创建语句的含义。公式 $\phi$ 的语义，其中命题符号为 $p_{1},\ldots ,p_{n}$，是一个映射，它将每个真值赋值 $V$ 到 $p_{1},\ldots ,p_{n}$ 关联到 $\phi$ 的一个真值（0 或 1）。（真值“真”和“假”可以分别用 1 或 0 代替，以及缩写“T”和“F”。）

由于事实 1（如上所示），语义是明确定义的。

指定逻辑连接词语义的一种方法是通过真值表

$p$	$q$	$p\land q$（p 且 q）
0	0	0
0	1	0
1	0	0
1	1	1

是否总能找到一个实现任何给定语义的公式？是的，任何真值表都可以由一个公式实现。该公式可以如下找到。“表示”其中 $\phi =1$ 的行，使用真命题符号的合取和假命题符号的否定。最后写出结果的析取。

例如，

$p$	$q$	$\phi$	合取（仅真值）
0	0	1	$\neg p\land \neg q$
0	1	0
1	0	1	$p\land \neg q$
1	1	0

$\phi :(p\land \neg q)\lor (\neg p\land \neg q)$

推论：每个公式都等价于命题符号或命题符号的否定构成的合取式的析取（析取范式，DNF）。

DNF 的对偶是合取范式，CNF。

要得到CNF 中的$\phi$

1. 描述$\phi$ 为假的场景。
2. 注意，当$\neg \psi$ 为假时，$\phi$ 为真。因此，使用德摩根定律对$\psi$ 取反。

在某些情况下，DNF（或 CNF）的大小会比原始公式指数级增长。例如，对于$(x_{1}\lor y_{1})\land \cdots \land (x_{n}\lor y_{n})$，其等价的 DNF 的大小是指数级的。

每个真值表是否都存在一个多项式大小的公式来实现它？更准确地说，是否存在$k$ 使得每个具有$n$ 个命题符号的真值表都存在一个大小为$\leq n^{k}$ 的形式$\phi$？答案：否。

证明：假设存在这样的$k$ 。对于$n$ 个命题符号，真值表的数量是$2^{2^{n}}$ 。大小为$\leq n^{k}$ 的公式数量是$(n+6)^{n^{k}}$（$n$ 个命题符号，4 个连接词和括号）。显然，$(n+6)^{n^{k}}<2^{2^{n}}$，对于足够大的$n$。

[待补充：解释这些定义是什么以及提供它们的上下文]

• 满足性：公式$\phi$ 被真值指派$\tau$ 满足。记号：$\tau \models \phi$（$\phi$ 对$\tau$ 为真）。
• 蕴涵：公式集$\Sigma$ 蕴涵$\phi$。记号：$\Sigma \models \phi$。$\Sigma$ 蕴涵$\phi$ 当且仅当每个满足$\Sigma$ 的真值指派也满足$\phi$。

特别感兴趣的公式类别

• ${\text{VALID}}$ – 公式集，其总是为真（也称为**重言式**）。例如，$(p\lor \neg p),(p\to p),([(p\lor q)\land (p\to q)]\to q)$ 是有效的公式。
• ${\text{UNSAT}}$ – 公式集，其永远为假（不可满足）。
• 介于两者之间：${\text{SAT}}$ - 公式集，其存在满足赋值（不可满足）。

注意。 $\phi \in {\text{VALID}}\iff \neg \phi \in {\text{UNSAT}}$。

断言：$\Sigma \models \phi \iff (\Sigma \cup \{\neg \phi \})\in {\text{UNSAT}}$

断言：${\text{SAT}}$ 是NP完全的。

证明:

• ${\text{SAT}}\in {\text{NP}}$ : 猜测一个满足赋值，然后验证公式是否为真（满足赋值是一个证书）。

• 硬度。图3着色 $\in {\text{NP}}$（也存在一个直接证明）。我们将3着色规约到 ${\text{SAT}}$。令 $G=(V,E)$ 为一个图，其中有 $n$ 个节点 $\{1,\ldots ,n\}$。我们使用命题变量 $p_{i,g},p_{i,r},p_{i,b}$ 来表示节点 $i$ 被染成绿色、红色或蓝色。构造 $\phi$ 如下

${\begin{aligned}\phi =&\bigwedge _{i=1}^{n}{\bigl (}(p_{i,g}\land \neg p_{i,r}\land \neg p_{i,b})\lor (p_{i,r}\land \neg p_{i,g}\land \neg p_{i,b})\lor (p_{i,b}\land \neg p_{i,r}\land \neg p_{i,g}){\bigr )}\\&\wedge \bigwedge _{(i,j\in E)}\neg (p_{i,g}\land p_{j,g})\land \neg (p_{i,r}\land p_{j,r})\land \neg (p_{i,b}\land p_{j,b})\end{aligned}}$

断言： $G\in {\text{3-Coloring}}\iff \phi \in {\text{SAT}}$。

也可以直接证明 ${\textrm {SAT}}\in {\text{NP}}$。

断言： ${\text{VALID}}\in {\text{coNP}}$。

Horn子句

SAT在多项式时间内解决的特殊情况。示例

$(p\lor \neg q\lor r)\land (\neg p\lor q\lor \neg r)$

**霍恩子句**（Horn clause）是指最多只有一个肯定文字（positive literal）的文字析取式（disjunction of literals）。霍恩子句主要有两种类型。

1. 子句包含1个肯定文字
   1. $p$，或者
   2. $p\lor \neg x_{1}\lor \cdots \lor \neg x_{k}:x_{1}\land \cdots \land x_{k}\to p$
2. 不包含肯定文字
   1. $\neg x_{1}\lor \cdots \lor \neg x_{k}:\neg (x_{1}\land \cdots \land x_{k})$
   2. $x_{1}\land \cdots \land x_{k}\to {\text{false}}$

**断言**：对于任意一组霍恩公式集$\Sigma$，检查$\Sigma$ 是否可满足（satisfiable）属于**P**类问题。

证明思路：令$\Sigma _{1}$ 为 $\Sigma$ 的子集，其中仅包含类型 1 的子句，而 $\Sigma _{2}$ 为 $\Sigma$ 的子集，其中包含类型 2 的子句。首先要注意的是，$\Sigma _{1}$ 是可满足的。为了得到一个最小满足赋值 $\sigma$，从单文字子句中的文字开始，并应用规则。现在需要检查 $\sigma$ 与 $\Sigma _{2}$ 中的子句的一致性。为此，只需检查对于 $\Sigma _{2}$ 中的每个子句 $x_{1}\land \cdots \land x_{k}\to {\text{false}}$，$\sigma$ 对于所有的 $x_{1},\ldots ,x_{k}$ 都不为真。

示例：考虑霍恩子句集 $\Sigma$

${\begin{aligned}&p\\&q\\&r\\&\neg p\lor \neg q\lor s\\&\neg s\lor \neg r\lor t\\&\neg t\end{aligned}}$

类型 1 的子句集 $\Sigma _{1}$ 由前 5 个子句组成，而 $\Sigma _{2}$ 由最后一个子句组成。请注意，$\Sigma _{1}$ 也可以写成

${\begin{aligned}&p\\&q\\&r\\&p\land q\to s\\&s\land r\to t\end{aligned}}$

对于 $\Sigma _{1}$，其最小满足赋值如下获得

1. 从 $\{p,q,r\}$ 开始
2. 利用第一个蕴含式推导出 $s$
3. 利用第二个蕴含式推导出 $t$

因此，最小满足赋值使得 $\{p,q,r,s,t\}$ 为真。这与 $\Sigma _{2}$ 矛盾，后者指出 $t$ 必须为假。因此，$\Sigma$ 不可满足。

演绎系统

**演绎**系统是一种从给定陈述中证明新陈述的机制。

令 $\Sigma$ 为一组已知的有效陈述（命题公式）。在演绎系统中，有两个组成部分：推理规则和证明。

推理规则

推理规则表明，如果某些陈述（公式）集 $\varphi _{1},\ldots ,\varphi _{k}$ 为真，则给定陈述 $\varphi$ 也必须为真。推理规则 $H$ 表示为 $H:{\frac {\varphi _{1},\ldots ,\varphi _{k}}{\varphi }}$。

示例（肯定前件）： ${\frac {p,~~p\to q}{q}}$

证明

从$\Sigma$中证明$\varphi$的证明是一个公式序列$\varphi _{1},\ldots ,\varphi _{n}$，其中$\varphi _{n}=\varphi$，并且对于所有$i\leq n$

• 每个公式$\varphi _{i}\in \Sigma$，或者
• 存在公式的子集$\varphi _{i_{1}},\ldots ,\varphi _{i_{k}}:i_{1},\ldots ,i_{k}<i$，使得${\frac {\varphi _{i_{1}},\ldots ,\varphi _{i_{k}}}{\varphi _{i}}}$是一个推理规则。

如果$\varphi$使用推理规则$H$从$\Sigma$ 有一个证明，我们写成$\Sigma \vdash _{H}\varphi$。

性质:

• 可靠性（Soundness）：如果$\Sigma \vdash _{H}\varphi$，则$\Sigma \models \varphi$（即，所有可证明的句子都是真的）。此属性对于演绎系统正确性的基础。
• 完备性（Completeness）：如果$\Sigma \models \varphi$，则$\Sigma \vdash _{H}\varphi$（即，所有真句子都是可证明的）。这是演绎系统中一个理想的性质。

自然演绎

自然演绎是一组推理规则。令$\perp$表示矛盾，假。以下是自然演绎的推理规则

1. $\left\{{\frac {\varphi ,\psi }{\varphi \land \psi }}\right.$
2. $\left\{{\frac {\varphi \land \psi }{\varphi }}\right.$}
3. $\left\{{\frac {\varphi \land \psi }{\psi }}\right.$}
4. $\left\{{\frac {\varphi ,\varphi \to \psi }{\psi }}\right.$}
5. $\left\{{\frac {\varphi ,\neg \varphi }{\perp }}\right.$}
6. $\left\{{\frac {\neg (\neg \varphi )}{\varphi }}\right.$}
7. $\left\{{\frac {\perp }{\varphi }}\right.$}
8. $\left\{{\frac {\varphi \to \psi ,\psi \to \varphi }{\varphi \leftrightarrow \psi }}\right.$}
9. $\left\{{\frac {\varphi \leftrightarrow \psi }{\varphi \to \psi }}\right.$}
10. $\left\{{\frac {\varphi \leftrightarrow \psi }{\psi \to \varphi }}\right.$}
11. $\left\{{\frac {\varphi }{\varphi \lor \psi }}\right.$}
12. $\left\{{\frac {\psi }{\varphi \lor \psi }}\right.$}
13. ${\begin{cases}{\dfrac {\begin{matrix}\varphi \\\vdots \\\psi \end{matrix}}{\varphi \to \psi }}\end{cases}}$}

14. ${\begin{cases}{\dfrac {\begin{matrix}\varphi \\\vdots \\\perp \end{matrix}}{\neg \varphi }}\end{cases}}$
15. ${\begin{cases}{\dfrac {\begin{matrix}\neg \varphi \\\vdots \\\perp \end{matrix}}{\varphi }}\end{cases}}$
16. ${\begin{cases}{\dfrac {\begin{matrix}\varphi \lor \psi &\varphi &\psi \\&\vdots &\vdots \\&\rho &\rho \end{matrix}}{\rho }}\end{cases}}$

规则 (13) 允许我们证明形如“如果 $\varphi$ 则 $\psi$” 的有效陈述，即使我们不知道 $\varphi$ 陈述的真值（即，$\varphi$ 不在已知有效陈述的集合 $\Sigma$ 中）。实际上，对于此规则，我们首先假设 $\varphi$ 是有效的。如果我们可以在 $\Sigma \cup \varphi$ 有效的世界中得出结论 $\psi$ 是有效的，那么我们得出结论关系 $\varphi \to \psi$ 为真，并且我们“释放”假设 $\varphi$ 是有效的。

现在我们展示如何应用上述推理规则。

示例：否定的或表达式的德摩根定律指出

$\neg (\varphi \lor \psi )\leftrightarrow (\neg \varphi \land \neg \psi )$

证明：根据规则 $(8)$，如果我们能证明 $\neg (\varphi \lor \psi )\to (\neg \varphi \land \neg \psi )$ 和 $(\neg \varphi \land \neg \psi )\to \neg (\varphi \lor \psi )$，我们就可以推导出期望的结果。

为了证明第一个方向，我们使用规则 13 并假设前提 $\neg (\varphi \vee \psi )$。然后

$\neg (\varphi \lor \psi )$ （假设）

$\varphi$ （假设）

$\varphi \lor \psi$ （根据规则11）

$\perp$ （根据规则5）

$\neg \varphi$ （根据规则14）

$\psi$ （假设）

$\varphi \lor \psi$ （根据规则11）

$\perp$ （根据规则5）

$\neg \psi$ （根据规则14）

$\neg \varphi \land \neg \psi$ （根据规则1）

$\neg (\varphi \lor \psi )\to (\neg \varphi \land \neg \psi )$ （根据规则13）

我们现在证明第二个方向。

$\neg \varphi \land \neg \psi$ （假设）

$\neg \varphi$ （根据规则2）

$\neg \psi$ （根据规则3）

$\varphi \lor \psi$ （假设）

$\varphi \psi$ （假设）

$\perp \perp$ （根据规则5）

$\perp$（根据规则16）

$\neg (\varphi \lor \psi )$ （根据规则14）

$(\neg \varphi \land \neg \psi )\to \neg (\varphi \lor \psi )$ （根据规则13）

皮尔斯定律的证明

$[(A\to B)\to A]\to A$

$(A\to B)\to A$ （假设）(1*)

$\neg A$ （假设）

$A$ （假设）

$\perp$ （根据规则5）

$B$ （根据规则7）

$A\to B$ （根据规则13）

$A$ （根据假设(1*)和规则4）

$\perp$ （根据规则5）

$A$ （根据规则14）

$[(A\to B)\to A]\to A$ （根据规则13）

事实2：自然演绎是可靠的。

为了证明自然演绎也是完备的，我们需要引入命题归结。

命题归结

归结是另一种用于检查语句有效性的过程。它涉及子句、公式和单个归结规则。

一些术语

子句

子句是由文字析取组成的命题公式。例如 $p\lor q\lor \neg r$ 。它通常表示为文字的集合，例如 $\{p,q,\neg r\}$ 。

空子句，表示为一个空框“$\Box$”，是没有文字的析取。它总是假的。

公式

一组子句，每个子句都是可满足的。例如，${\bigl \{}\{p,\neg q\},\{r\},\{\neg r,s\}{\bigr \}}$表示CNF公式 $(p\lor \neg q)\land (r)\land (\neg r\lor s)$。

空公式，表示为 $\varnothing$ ，是不包含任何子句的集合。它总是真的。

归结规则

规则规定，给定两个子句$C$（包含某个文字$y$）和$C'$（包含某个文字$\neg y$），可以推导出一个新的子句，称为$C$和$C'$的结果子句（相对于$y$）。

归结证明系统包含单个归结规则，其中结果子句定义如下。假设$C$和$C'$是子句，使得$y\in C$且$\neg y\in C'$，则

${\text{Res}}_{y}(C,C')=(C-\{y\})\cup (C'-\{\neg y\})$

包含$\varphi$且在归结下封闭的最小子句集记为${\text{Res}}(\varphi )$。

示例：如果$C=\{p,y\}$且$C'=\{q,\neg y\}$，则${\text{Res}}_{y}(C,C')=\{p,q\}$。

可以证明，如定义的那样，归结规则计算出的子句可以通过自然演绎推导出来。

断言：设 $C$ 和 $C'$ 是任意两个子句，使得 $y\in C$ 且 $\neg y\in C'$ 。则 $C\land C'\implies {\text{Res}}_{y}(C,C')$ 。

为了证明一个陈述 $\psi$ 的有效性，我们将证明其否定陈述 $\neg \psi$ 是不可满足的。为了证明公式 $\varphi$ 的不可满足性，我们需要定义公式 $\varphi$ 的归结反驳。

公式 $\varphi$ 的归结反驳树是一棵根节点为空子句的树，其中每个叶子节点都是 $\varphi$ 中的一个子句，每个内部节点都计算为其两个对应子节点的归结式。

注意，$\varphi$ 的子句可以重复作为叶子节点出现。根据上述断言，我们可以得出结论：

断言：如果存在公式 $\varphi$ 的归结反驳树，则 $\varphi \implies \Box$ ，也就是说，$\varphi$ 是不可满足的。

示例：公式

$\varphi =(p\lor q)\land (\neg q\lor r)\land (\neg r)\land (\neg p\lor \neg s)\land (s\lor \neg t)\land (t)$

具有以下归结反驳树

在计算归结反驳树时，选择子句计算归结式的顺序很重要，如下例所示：考虑公式

$\psi =(p\lor q)\land (\neg q\lor r)\land (\neg p)\land (\neg q)$

即使对于$\psi$可能存在归结反驳树，但在尝试构建树时，顺序也很重要。下面是两个不同的归结反驳树，但只有一个是成功的。

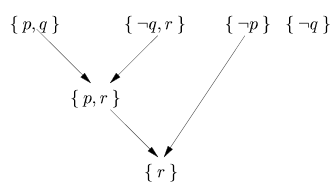对$\psi$进行归结反驳树的不成功尝试

对$\psi$进行归结反驳树的成功尝试

命题归结的性质

可靠性：命题归结是可靠的，也就是说，如果对于给定的公式$\varphi$存在归结反驳树，则$\varphi$必须是不可满足的。

定理：对于任何公式$\varphi$，如果$\Box \in Res(\varphi )$，则$\varphi \implies \Box$。

完备性：命题归结是完备的，也就是说，如果给定的公式$\varphi$是不可满足的，则$\varphi$具有归结反驳树。

定理：对于任何公式$\varphi$，如果$\varphi \implies \Box$，则$\Box \in Res(\varphi )$。

证明：通过对$\varphi$中变量个数进行归纳。

基础情况：我们有一个变量，比如$p$。$\varphi$的所有可能的子句是$\{p\}$和$\{\lnot p\}$。如果$\varphi$是不可满足的，则这两个子句都会出现，因此$\Box \in Res(\varphi )$。

归纳步骤：假设对于少于$n$个变量的公式，该假设成立。令$\varphi$为一个具有$n$个变量的公式。假设$\Box \notin Res(\varphi )$；我们将证明$\varphi$是可满足的。令$p$为$\varphi$的一个变量。那么要么$\{p\}\notin Res(\varphi )$，要么$\{\lnot p\}\notin Res(\varphi )$（如果两者都成立，则$\Box \in Res(\varphi )$立即成立）。

假设$\{\lnot p\}\notin Res(\varphi )$。我们定义公式$\varphi ^{p}$，它包含所有不包含$\{p\}$的子句，并且其中文字$\lnot p$已从每个子句中删除（换句话说，$\varphi ^{p}$等价于将$p$设置为真的结果得到的公式）。

形式上，

$\varphi ^{p}=\{C-\{\lnot p\}:C\in \varphi ,\,p\notin C\}$.

首先，注意

$Res(\varphi ^{p})=\{C-\{\lnot p\}:C\in Res(\varphi ),\,p\notin C\}$

因此，

$\{\lnot p\}\notin Res(\varphi ^{p})$.

此外，由于 $\Box \notin Res(\varphi )$，我们有 $\Box \notin Res(\varphi ^{p})$。根据归纳假设，$\varphi ^{p}$ 是可满足的。然后 $\varphi$ 通过 $\varphi ^{p}$ 的满足赋值的扩展来满足，其中 $p$ 等于真。情况 $\{p\}\in Res(\varphi )$ 类似。

自然演绎的完备性

定理：令 $H$ 为自然演绎的推理规则集。如果 $\Sigma \models \varphi$，则 $\Sigma \vdash _{H}\varphi$。

自然演绎完备性证明的思想如下。假设 $\varphi$ 是有效的（那么 $\lnot \varphi$ 是不可满足的）。然后我们证明存在一个针对 $\varphi$ 的归结反驳，然后通过应用矛盾规则（规则 15）

${\frac {\begin{matrix}\neg \varphi \\\vdots \\\perp \end{matrix}}{\varphi }}$

我们得出结论 $\varphi$ 可以被推断出来。

证明：（草图）给定一个在 $\Sigma$ 下有效的公式 $\varphi$，我们执行以下步骤

1. 证明 $\lnot \varphi$ 等价于某个 $\psi$，其中 $\psi$ 为合取范式。
2. 证明对于所有 $\psi$，都有 $\psi \implies Res(\psi )$ 成立。
3. 根据归结原理的完备性，如果 $\psi$ 是不可满足的，则 $\Box \in Res(\psi )$。因此，对于某个文字 $p$，有 $\{p\}$ 和 $\{\lnot p\}\in Res(\psi )$。这意味着 $Res(\psi )\implies \bot$。
4. 得出结论 $\lnot \varphi \implies \bot$，因此 $\varphi$ 是有效的。

步骤 (1) 可以通过重复应用德摩根定律轻松完成。步骤 (2) 可以使用自然演绎法证明。最后，步骤 (3) 可以通过对获得 $Res(\psi )$ 的步骤数进行归纳证明。显然，每个步骤都可以使用自然演绎法模拟。

任何命题归结算法在最坏情况下都可能需要很长时间（回想一下，检查公式 $\varphi$ 的有效性是 co-NP 完全的）。

线性归结和 PROLOG

线性归结是一种特殊的归结策略，它总是将最新的归结式与一个子句进行归结。因此，由此获得的归结反驳树是线性的。可以证明，如果子句集是 Horn 子句，则对于任何公式都存在一种线性归结策略。也就是说，线性归结对于 Horn 子句集是完备的。

PROLOG 语言使用霍恩子句集上的归结原理。每个子句称为程序子句。此外，由单个文字组成的子句称为事实。只有一个否定文字的子句称为查询。下表显示了不同表示法的比较。在 PROLOG 中，要查询语句$t$，其思路是将语句取反（$\lnot t$），并使用已知真语句集执行归结。如果找到一个归结反驳树，则语句$t$ 由程序蕴含。

示例：线性归结用于公式的示例

$\phi =(p)\land (q)\land (r)\land (t\lor \lnot s\lor \lnot r)\land (s\lor \lnot p\lor \lnot q)\land (\lnot t)$

如下所示