在命题情况下,我们通过“去除”两个要进行归结的子句中的一对互补文字来定义归结推理规则。然而,在一阶情况下,这并不总是足够的。

在这两个子句中,没有互补文字,但是,在将项 替换为变量
替换为变量 在
在 和将
和将 替换为
替换为 在
在 后,我们得到
后,我们得到

现在我们可以应用命题逻辑中的推理规则,并得到归结式 。
。
另一种可能性是将 替换为
替换为 在
在 中,得到
中,得到

然后我们可以得到从 和
和 的
的 解,从某种意义上说,它比之前推导出的解更通用。
解,从某种意义上说,它比之前推导出的解更通用。
替换 是一个函数,它将变量映射到项,并且几乎处处都是恒等映射。因此,它可以表示为
是一个函数,它将变量映射到项,并且几乎处处都是恒等映射。因此,它可以表示为

如果 是基本项,我们称
是基本项,我们称 为基本替换。空替换用
为基本替换。空替换用 表示。
表示。
令 为一个替换,且
为一个替换,且 为一个表达式(即文字或项),则
为一个表达式(即文字或项),则 是从
是从 中同时替换
中同时替换 中每个出现的
中每个出现的 得到的表达式,用项
得到的表达式,用项 替换。
替换。
示例
当

且

时,我们得到

设  和
和  是两个代换。则代换的复合,记为
是两个代换。则代换的复合,记为  ,是从
,是从  中删除任何满足
中删除任何满足  的元素
的元素  和任何满足
和任何满足  的元素
的元素  所得到的代换。
所得到的代换。
示例
设  是一个表达式集合,且
是一个表达式集合,且  是一个代换,
是一个代换, 是
是  的一个统一化子,当且仅当
的一个统一化子,当且仅当

.
一个统一代换  被称为最一般统一代换,当且仅当对于每个统一代换
被称为最一般统一代换,当且仅当对于每个统一代换  ,都存在一个替换
,都存在一个替换  使得
使得  。
。
接下来,我们将讨论一种计算最一般统一代换的算法。为此,我们假设有一组要进行统一的项  。首先,我们通过引入一个尚未出现在此集合中的新变量,例如
。首先,我们通过引入一个尚未出现在此集合中的新变量,例如  ,并将此集合转换为一组方程。
,并将此集合转换为一组方程。

我们现在将转换此集合,使其统一代换保持不变,其中  是一组
是一组  的统一代换,如果
的统一代换,如果  成立。
成立。
统一
给定一组表达式。将其转换为一组如上定义的方程  。尽可能地应用以下转换规则
。尽可能地应用以下转换规则
 方向化
方向化
其中  是一个变量,而
是一个变量,而  是一个非变量项
是一个非变量项
 删除
删除
 分解 (项约简)
分解 (项约简)
![{\displaystyle {\frac {R\uplus \{x=t\}}{R[x/t]\uplus \{x=t\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b00afc306f39edb6d78dd4dd9cf1882d8d2aed33) 消去 (变量消去 I)
消去 (变量消去 I)
如果  不在
不在  中,但在
中,但在  中
中
![{\displaystyle {\frac {R\uplus \{x=y\}}{R[x/y]\uplus \{x=y\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3375d2f6a69e886d488026b47fd1c7a5ecf41413) 合并 (变量消去 II)
合并 (变量消去 II)
如果  在
在  中
中
 冲突
冲突
如果  或
或 
 出现检查
出现检查
如果  在
在  中
中
设  为一组表达式。上述统一算法会终止。如果它返回
为一组表达式。上述统一算法会终止。如果它返回  ,则
,则  没有统一式,否则
没有统一式,否则  会被转换为一组方程
会被转换为一组方程  ,它表示
,它表示  的最一般统一式。
的最一般统一式。
如果一个子句  的两个或多个文字具有一个统一式
的两个或多个文字具有一个统一式  ,则
,则  称为
称为  的一个因子。
的一个因子。
示例
对于

和

,我们得到因子

设 和
和  是两个没有公共变量的子句,使得
是两个没有公共变量的子句,使得  且
且  ,并且
,并且  和
和  有一个最一般合一化
有一个最一般合一化  。
。  和
和  的二元消解式是
的二元消解式是

示例:给定  和
和  。将
。将  重命名为
重命名为  ,通过使用最一般合一化
,通过使用最一般合一化  ,得到消解式
,得到消解式  。
。
我们通常以图形方式描绘消解式,例如:

两个子句  和
和  的消解式是以下二元消解式之一
的消解式是以下二元消解式之一
 和
和  的二元消解式
的二元消解式 的二元消解式和
的二元消解式和  的一个因子
的一个因子 的一个因子的二元消解式和
的一个因子的二元消解式和 
 的一个因子的二元消解式和
的一个因子的二元消解式和  的一个因子的二元消解式
的一个因子的二元消解式
示例
给定

和

。
 的一个因子是
的一个因子是  。
。  和
和  的二元消解式,因此也是
的二元消解式,因此也是  和
和  的二元消解式是
的二元消解式是  。
。
下面的引理用于消解完备性证明。
如果 和
和  分别是
分别是  和
和  的实例,并且
的实例,并且  是
是  和
和  的一个解,那么存在
的一个解,那么存在  和
和  的一个解
的一个解  ,使得
,使得  是
是  的一个实例。
的一个实例。
 图 1
图 1
一个子句集  是不可满足的,当且仅当空子句可以通过归结原理从
是不可满足的,当且仅当空子句可以通过归结原理从  推导出。
推导出。
证明
假设  是不可满足的。令
是不可满足的。令  为
为  的基本原子集,因此是 Herbrand 基。令
的基本原子集,因此是 Herbrand 基。令  为一棵完整的二叉树,如 图 2 所示。根据 Herbrand 定理(版本 1),存在一棵封闭的有限语义树
为一棵完整的二叉树,如 图 2 所示。根据 Herbrand 定理(版本 1),存在一棵封闭的有限语义树  。有两种情况
。有两种情况
- 如果
 只包含一个节点(因此是根节点),则从这棵树的空分支收集的解释只使空子句为假。因此,空子句必须在
只包含一个节点(因此是根节点),则从这棵树的空分支收集的解释只使空子句为假。因此,空子句必须在  中。
中。
- 假设
 包含多个节点。那么,
包含多个节点。那么, 中一定存在一个推理节点
中一定存在一个推理节点 ,因此它的两个子节点
,因此它的两个子节点 和
和 都是失败节点。如果这样的节点不存在,那么每个节点都至少有一个非失败节点,这意味着在
都是失败节点。如果这样的节点不存在,那么每个节点都至少有一个非失败节点,这意味着在 中至少存在一条无限路径,这将违反它是一个有限闭合语义树的事实。设
中至少存在一条无限路径,这将违反它是一个有限闭合语义树的事实。设 如上所述;并设
如上所述;并设
现在,令 和
和  分别是子句
分别是子句  和
和  的基本实例,使得
的基本实例,使得  被
被  证伪,而
证伪,而  被
被  证伪,使得两者均不被
证伪,使得两者均不被  证伪。
证伪。
因此,我们有  和
和  ,并且我们可以构造归结式
,并且我们可以构造归结式

 must be false in
must be false in  , because both
, because both  and
and  are false in
are false in  . According to the Lifting Lemma 5 there exists a resolvent
. According to the Lifting Lemma 5 there exists a resolvent  of
of  and
and  , such that
, such that  is a ground instance of
is a ground instance of  . Let
. Let  be the closed semantic tree for
be the closed semantic tree for  , obtained from
, obtained from  by deleting all nodes below the first node which falsifies
by deleting all nodes below the first node which falsifies  . Note, that
. Note, that  is unsatisfiable if and only if
is unsatisfiable if and only if  is unsatisfiable. Clearly,
is unsatisfiable. Clearly,  has less nodes than
has less nodes than  and we now can iterate this process until only the root of the semantic tree is remaining. This, however is only possible if the empty clause
and we now can iterate this process until only the root of the semantic tree is remaining. This, however is only possible if the empty clause  is derivable. For the opposite direction, assume that
is derivable. For the opposite direction, assume that  is derivable by resolution from
is derivable by resolution from  and let
and let  the resolvents constructed during this process. Assume
the resolvents constructed during this process. Assume  is satisfiable and
is satisfiable and  to be a model for
to be a model for  . From the correctness lemma according to the propositional case we known, that if a model satisfies two clauses it also satisfies its resolvent. Therefore
. From the correctness lemma according to the propositional case we known, that if a model satisfies two clauses it also satisfies its resolvent. Therefore  has to satisfy
has to satisfy  ; this, however, is impossible, because one of this resolvents is
; this, however, is impossible, because one of this resolvents is  .
.
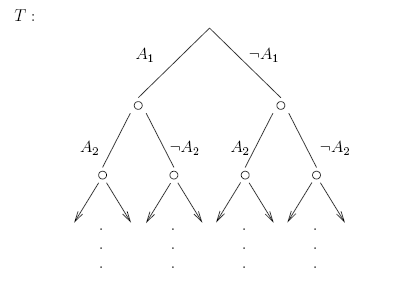
图 2
在每种情况下,用谓词逻辑归结法推导出空子句!


(

)


通过对项和公式构造的归纳,展示以下的提升引理:如果 是一个谓词逻辑公式,并且
是一个谓词逻辑公式,并且 是一个适合
是一个适合 的解释,
的解释,
以及![{\displaystyle F[x/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f6c858d274f9d292d0d8348142a04658048d3e) 。那么
。那么
![{\displaystyle {\mathcal {I}}(F[x/t])={\mathcal {I}}_{[x/{\mathcal {I}}(t)]}(F),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af8c733f03d88cddf67e35e698af3075c6d6415b)
是有效的,如果 不包含任何被
不包含任何被![{\displaystyle [x/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff5a99a8641a9e4e67622b7b0e152230a5f72ed1) 在
在 中的替换所绑定的变量。
中的替换所绑定的变量。
通过替换绑定。

计算 - 如果可能 - 以下子句集的最一般统一。





确定以下子句对的所有直接消解式
 和
和 
 和
和 
 和
和 
 和
和 

计算 - 如果可能 - 以下子句集的最一般统一。





确定以下子句对的所有直接消解式
- {¬p(x), ¬p(b), q(x,b)} 和 {p(a), q(a,b)}
- {r(x), r(f(x))} 和 {¬r(x), ¬r(f(f(x)))}
- {¬s(c,g(c))} 和 {s(x,x), ¬t(x)}

对于以下子句集,给出(a)线性推导,(b)使用单元分解的推导,(c)通过谓词逻辑分解获得空子句的进一步(最短)推导!
{{¬e(x), o(s(x))}, {¬e(x), ¬o(s(x)), e(s(s(x)))}, {e(a)}, {¬o(s(s(s(s(s(a))))))}}

在每种情况下,用谓词逻辑归结法推导出空子句!


(

)




















































![{\displaystyle {\frac {R\uplus \{x=t\}}{R[x/t]\uplus \{x=t\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b00afc306f39edb6d78dd4dd9cf1882d8d2aed33)

![{\displaystyle {\frac {R\uplus \{x=y\}}{R[x/y]\uplus \{x=y\}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3375d2f6a69e886d488026b47fd1c7a5ecf41413)





























































![{\displaystyle F[x/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f6c858d274f9d292d0d8348142a04658048d3e)
![{\displaystyle {\mathcal {I}}(F[x/t])={\mathcal {I}}_{[x/{\mathcal {I}}(t)]}(F),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af8c733f03d88cddf67e35e698af3075c6d6415b)
![{\displaystyle [x/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff5a99a8641a9e4e67622b7b0e152230a5f72ed1)














