计算机科学家逻辑/命题逻辑/预备知识

预备知识

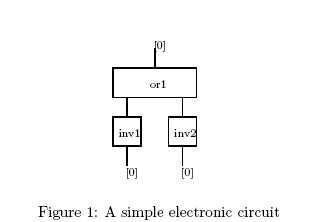
作为一个运行的例子，考虑图 1 中的简单数字电路，它包含一个或门 ($or1$) 和两个反相器 ($inv1$ 和 $inv2$)。系统描述由以下命题公式给出，其中公式按顺序标记以方便识别图 1 中的对应部分。公式中使用的助记符如下

• 符号 $\lor$，$\land$ 和 $\lnot$ 分别表示“或”、“与”和“非”。
• $i1$ 和 $i2$ 表示或门的输入，$i$ 表示反相器，$o$ 表示门的输出。
• $high$ 是一个谓词，它用于表示其参数指定的值“处于高电压”，即处于开启状态。
• $ab$ 是一个谓词，表示“异常”，即表达式 $\lnot (ab(inv1))$ 可以理解为“反相器一没有异常”。

$OR1:{\lnot (ab(or1))\to high(or1,o)\leftrightarrow (high(or1,i1)\lor high(or1,i2))}$
$INV1:{\lnot (ab(inv1))\to high(inv1,o)\leftrightarrow \lnot (high(inv1,i))}$
$INV2:{\lnot (ab(inv2))\to high(inv2,o)\leftrightarrow \lnot (high(inv2,i))}$
$CONN1:{high(inv1,o)\leftrightarrow high(or1,i1)}$
$CONN2:{high(inv2,o)\leftrightarrow high(or1,i2)}$

这些公式包含表达其预期含义的标签：OR1 代表描述或门功能的公式，IN1 和 IN2 描述了两个反相器（相同）的行为：CONN1 和 CONN2 指定了或门输入与反相器输出的连接方式。注意，在此描述中，系统的输入和输出尚未定义。从图形描述中我们可以观察到，电路的两个输入都具有低电压，输出也具有低电压，即我们可以通过公式 $\lnot high(inv1,i),\;\lnot high(inv2,i),\;$ $\lnot high(or1,o)$ 来描述这一点。

此示例演示了如何使用诸如 $high(inv1,o)$ 这样的命题来正式描述电子电路的行为。请注意 $high(inv1,o)$ 可以直观地理解为“反相器 1 的输出为高”，当然，这句句子可以通过忽略词组结构并将其理解为一个简单的字符串来进一步简化：“反相器 1 的输出为高”。如果我们对其他命题也采用同样的方式进行处理，我们将得到这样的公式。

反相器 1 的输出为高 $\leftrightarrow$ 反相器 1 的输入为高

此公式包含两个通过双箭头连接的命题。可以很容易地看出，这种方式会导致公式变得很长，因此我们可以通过更简单的字符串（例如 $P_{1}$ 或 $P_{2}$）来进一步缩写命题，从而得到公式 $P_{1}\leftrightarrow P_{2}$。通过上述论证应该清楚，对于我们的目的而言，此公式与 $high(or1,i1)\leftrightarrow high(inv1,o)$ 传达的信息相同。唯一的区别是，后者与读者联系在一起一些直觉，而对于我们形式逻辑框架而言，这无关紧要，我们将专注于任意命题。

在接下来的内容中，我们将系统地避免在语言设计中引入任何与现实世界含义相关的直觉。我们将专注于研究可以通过我们的语言表达的逻辑方面，而不是某个特定的预期含义。换句话说，我们之前介绍的用于描述玩具电子电路的逻辑公式，过于依赖于由图片引发的解释。

我们将通过一个非常简单的归纳定义来介绍命题逻辑的语法，然后通过另一个单独的定义来指定形式语义。