枫叶/与相对论相关的方程绘图

变量赋值和绘图都是简单的枫叶函数，它们非常重要，可以用于各种目标，无论是为使方程式更容易使用而为物理常量赋值，还是使对 1000 个项的数据集进行绘图的任务更加易于管理。在这里，我们将使用与狭义相对论相关的方程式来演示这些简单的命令。

绘制 e=mc^2 图像

E=mc^2 是一个非常著名的方程式，它描述了能量和质量之间的关系。完整的方程式包含一个伽马函数，它根据速度基本修改了答案。该图表明，当速度接近光速时，能量接近无穷大。

1. 将 c 赋值为 1。（尽管光速 'c' 在狭义相对论中实际上接近 3*10^8 m/s，但我们使用将它设为 1 的约定，这样当我们使用非常大的速度时，我们可以将它们赋值为光速的几分之一。例如，v=0.5 是光速的一半）

2. 赋值函数： $\gamma (v)={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}$

3. 赋值函数： $E(v,m)=\gamma (v)\,m\,{c}^{2}$

4. 在 m= 0 到 0.9 的范围内绘制 E(v,30) 图像。为了标记 y 轴，请在 maple 绘图命令中将您想要的标签作为第三个项输入，在指定范围之后。参见下文。另请参见如何添加标题。

解决方案（枫叶命令）

c:=1;
Gamma:= (v)-> 1/sqrt(1-(v**2/c**2));
E:= (v,m)-> Gamma(v) * m * c**2;
plot(E(v,30), v=0..0.9, energy, title="Energy Mass Relationship");

绘制长度收缩方程图像

狭义相对论理论解释了，从另一个参考系观察到的物体的长度在其沿长度方向运动时会收缩。实际上，当物体的相对速度接近光速时，物体的长度接近零。从理论上讲，物体永远不会真正达到光速。此方程式为 L_prime= L/Gamma。 L_prime 是收缩后的长度，L 是 '固有长度' 或在物体参考系中测量的长度。 Gamma 是上面的问题。绘制一辆 10 米长的轿车从 v=0 到 c 的 L_prime 图像。

解决方案

c:=1;
Gamma:= (v)-> 1/sqrt(1-(v**2/c**2));
L_prime:= (L,v)-> L/Gamma(v);
plot(L_prime(10,v),v=0..c, length, title="Length Contraction");

计算日常物体长度收缩

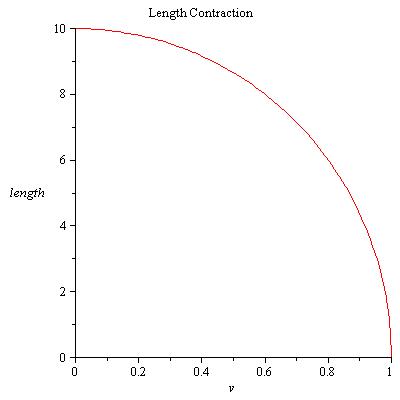
伽马在这些方程式中的作用本质上是修正因子，用于考虑不同值相对于物体运动速度的变化。长度变化不会影响我们的日常生活，因为我们周围的一切物体运动速度都太慢，无法影响我们感知的长度或时间。为了证明这一点，尝试将不同的速度代入 1 米长的物体的 L_prime 方程式，看看行人速度（约 1.5 m/s）、汽车速度（约 30 m/s）、X-43 火箭/超燃冲压发动机飞机速度（3,111 m/s）以及阿波罗 10 号重返大气层时的实际速度的 10,000 倍（11,100 m/s * 10,000）会产生多大的变化。使用光速的实际值作为 c，即 299,792,458 m/s。（通过使用 evalf 函数，它强制 maple 输出小数而不是繁琐的分数）。注意，即使在非常高的宇宙飞船速度下，变化也很小。

解决方案

L_prime:= (L,v)-> L/Gamma(v);
c:=299792458;
evalf(L_prime(1,1.5));
                                                           1.000000000
evalf(L_prime(1,30));
                                                           0.999999999
evalf(L_prime(1,3111));
                                                           0.999999999
evalf(L_prime(1,(11,100*10000)));
                                                           0.9290317539

可以看出，在我们能够达到的速度下，长度收缩可以忽略不计。速度
行走 - 1 米
汽车 - 1 米
飞机 - 1 米
阿波罗 10 号的 10,000 倍 - 0.93 米

相对论中的动能（每个图绘制多个函数）

对于日常情况，我们可以使用方程式 $E={\frac {m\,v^{2}}{2}}$ 来根据物体的质量和速度测量物体的动能。然而，狭义相对论告诉我们，当速度接近光速时，能量会增加到无穷大。更精确的方程式描述了非常高的相对速度下的动能，即 $E=\lambda \,m\,c^{2}-m\,c^{2}$ 。赋值这两个函数，然后将它们一起绘制在同一个图上，以显示牛顿动能方程式 (E=mv^2/2) 在非常高的速度下的误差。以光速的 10%、50% 和 100% 绘制这两个方程式的图像。请注意，直到非常高的速度，在两个方程式中计算出的能量的差异都可以忽略不计。

解决方案

kinetic:=(m,v)-> (1/2)*m*v**2; 

kinetic2:= (m,v)-> Gamma(v) * m * c**2- m*c**2; 

c:= 299792458; 

plot([kinetic2(13, v), kinetic (13,v)], v=0..(.1*c),kinetic_energy, title="Difference Between Newtonian and Relativistic Kinetic Energies at 10% c");

plot([kinetic2(13, v), kinetic (13,v)], v=0..(.5*c),kinetic_energy, title="Difference Between Newtonian and Relativistic Kinetic Energies at 50% c");

plot([kinetic2(13, v), kinetic (13,v)], v=0..c,kinetic_energy, title="Difference Between Newtonian and Relativistic Kinetic Energies at 100% c");