电子材料/受限粒子/一维无限势阱

一维无限势阱

通常，考虑电子“被困”在一个封闭空间中是方便的，例如在具有与其周围环境之间存在较大带隙的半导体材料中。这种电子陷阱称为“势阱”。理论上最简单的例子是一维无限势阱，其中电子完全受限且永远无法逃逸，因为这样做需要无限的能量。

我们稍后将将其扩展到更多维度以及更现实的有限势阱，其中电子可以逃逸。

现在，考虑一个被困在宽度为L的无限势阱中的电子（右图）。该系统的势能由下式给出

$V\left(x\right)={\begin{cases}\infty ,\quad x<0\\0,\quad \,\,\,0\leq x\leq L\\\infty ,\quad x>L\end{cases}}$

在该区域之外找到电子的概率为零。根据波函数条件，该势阱中电子的波函数必须是连续的，因此我们需要寻找一个在x=0和x=L处为零的ψ(x)解。如果不是这样，我们将在这里有一个不连续性。

求解波函数

我们需要求解薛定谔方程来找到ψ(x)

$-{\hbar ^{2} \over {2m}}{{d^{2}\psi \left(x\right)} \over {dx^{2}}}+V\left(x\right)\psi \left(x\right)=E\psi \left(x\right),\quad \quad 0\leq x\leq L$.

由于在这个区间上V(x)为零，我们可以写成

$-{\hbar ^{2} \over {2m}}{{d^{2}\psi \left(x\right)} \over {dx^{2}}}=E\psi \left(x\right)\quad \quad 0\leq x\leq L$.

重新排列，

${{d^{2}\psi \left(x\right)} \over {dx^{2}}}=-{{2mE} \over \hbar ^{2}}\psi \left(x\right)$

回想一下，能量由下式给出

$E\,$	$=T\left(x\right)+V\left(x\right)\,$
	$={{\hbar ^{2}k^{2}} \over {2m}}$

将E代入我们的微分方程，得到

${{d^{2}\psi \left(x\right)} \over {dx^{2}}}=-k^{2}\psi \left(x\right)$

这是一个标准形式的二阶微分方程。其通解为：

[General Solution]

$\psi \left(x\right)=A\sin {kx}+B\cos {kx}$

应用边界条件

应用第一个边界条件 $\left(\psi \left(0\right)=0\right)$

$\psi \left(0\right)=A\sin \left(0\right)+B\cos \left(0\right)=0$

因此，B=0。

应用第二个边界条件 $\left(\psi \left(L\right)=0\right)$

$\psi \left(L\right)=A\sin \left(kL\right)=0$

因此，kL必须是π的倍数。

$kL=n\pi \quad n=\{0,1,2,\ldots \}$

$k={\frac {n\pi }{L}}\quad n=\{0,1,2,\ldots \}$

我们称A为归一化系数，ψ₀。它的存在是为了确保在整个空间中找到电子的概率为1。此外，当n=0时，整个方程变为零，电子存在的概率为零，因此，一维盒子中粒子的薛定谔方程的解从n=1开始。

$\psi _{n_{x}}\left(x\right)=\psi _{0}\sin \left({{n_{x}\pi } \over L}x\right),\quad n_{x}=\left\{{1,2,3,\ldots }\right\}$

因为我们在x方向上工作，所以我们将索引号称为n_x。这被称为波数。与上述解相关的能量由下式给出：

$E_{n_{x}}$	$={{\hbar ^{2}k^{2}} \over {2m}}$
	$={{\hbar ^{2}n_{x}^{2}\pi ^{2}} \over {2mL^{2}}},\quad n_{x}=\left\{{1,2,3,\ldots }\right\}$

这里要注意两点。

• 只有当波数n为整数时，才能得到满足薛定谔方程的波函数。
• 每个波函数（本征函数）都与其特定的能量（本征值）相关联。该能量与波数的平方成正比，并与n=1、E₁时的波函数能量成正比。

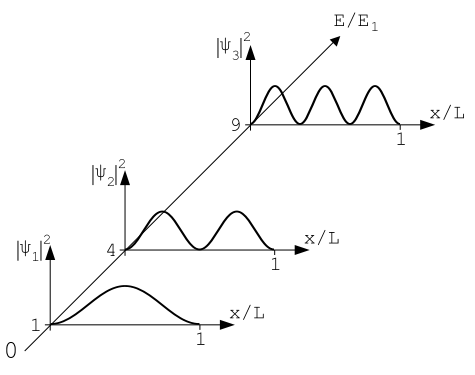
下图显示了波数为1、2和3的波函数，并相对于E₁绘制了相应的能量。

一旦找到波函数，就可以很容易地找到概率密度 - 只需取模数（对于复波函数）并平方即可。这将导致如下所示的概率密度。

归一化系数

我们可以利用电子一定存在于量子阱中的知识，以及概率密度函数下的面积为 1 的知识来求归一化系数 ψ₀

$\int \limits _{-\infty }^{\infty }{\left|{\psi \left(x\right)}\right|^{2}dx}=\int \limits _{0}^{L}{\psi \left(x\right)^{*}\psi \left(x\right)}dx=1$

因此，对于我们的波函数，$\psi _{n_{x}}\left(x\right)=\psi _{0}\sin \left({{n_{x}\pi } \over L}x\right)$,

$\int \limits _{0}^{L}{\psi _{0}^{2}\sin ^{2}\left({\frac {n_{x}\pi }{L}}x\right)dx}=1$

$\psi _{0}^{2}\int \limits _{0}^{L}{{\frac {1}{2}}\left(1-\cos \left({\frac {2n_{x}\pi }{L}}\right)x\right)dx}=1$

$\psi _{0}^{2}\left[\int \limits _{0}^{L}{{\frac {1}{2}}dx}-{\frac {1}{2}}\int \limits _{0}^{L}{\cos \left({\frac {2n_{x}\pi }{L}}x\right)dx}\right]=1$

$\psi _{0}^{2}\left[{\frac {L}{2}}-{\frac {L}{4n_{x}\pi }}\left[\sin \left({\frac {2n_{x}\pi }{L}}x\right)\right]_{0}^{L}\right]=1$

由于正弦曲线在一个完整周期的面积为零，所以我们有

$\psi _{0}^{2}{\frac {L}{2}}=1$

$\psi _{0}={\sqrt {\frac {2}{L}}}$

结果表明，这与波数无关，因此我们得到一维无限势阱中电子的归一化波函数在阱外为零，而在阱内由以下方程给出：

[一维无限势阱中粒子的波函数]

$\psi _{n_{x}}\left(x\right)={\sqrt {\frac {2}{L}}}\sin \left({{n_{x}\pi } \over L}x\right),\quad n_{x}=\left\{{1,2,3,\ldots }\right\}$

在阱内，相关的能量由以下公式给出：

[波函数相关的能量]

$E_{n_{x}}={{\hbar ^{2}\pi ^{2}} \over {2mL^{2}}}n_{x}^{2},\quad n_{x}=\left\{{1,2,3,\ldots }\right\}$