数学证明/集合论导论

在数学中，我们经常使用被称为**集合**的对象，并且存在研究它们的**集合论**。虽然集合论可以被正式讨论，但我们在这本书中不需要进行如此正式的讨论，而且在这个阶段我们可能对正式讨论不感兴趣也不理解。

即使我们不正式讨论集合论，了解一些关于集合的基本概念也很重要，这些概念将在本章中介绍。

什么是集合？

**集合**可以被看作是定义明确、不同对象的集合（这些对象也可以是集合）。由于“定义明确”一词的模糊性，我们不认为这是集合的定义。相反，我们将集合视为一个原始概念（即，没有用先前定义的概念来定义的概念）。数学中其他原始概念的例子包括**点**和**线**。

我们已经提到，集合是定义明确、不同对象的集合。集合中的对象被称为集合的**元素**。我们写$a\in A$表示元素$a$属于集合$A$。如果$a$不属于$A$，我们写$a\notin A$.

例子。

• 考虑所有偶数的集合$E$。E 的元素包括（但不限于） -2、0 和 4，即 $-2,0,4\in E$.
• 英语字母的元素（一个集合）是英语字母。

描述集合的方式

有多种方式可以精确地描述一个集合（在属于集合的元素被精确地知道的情况下）。

如果一个集合包含少量元素，那么列举法可能非常有效。在列举法中，集合的元素被列在一个花括号（{}）内。特别是，仅仅改变元素的顺序并不会改变所表示的集合。例如，$\{1,2\}$ 和 $\{2,1\}$ 都表示相同的集合，其元素为 1 和 2。如果花括号中列出的元素相同，则使用列举法在不同列举顺序下创建的符号表示相同的集合。此外，在集合中重复列举特定元素不会改变所表示的集合。例如，$\{1,1,2,2,2\}$ 和 $\{1,2\}$ 都表示相同的集合，其元素为 1 和 2。特别是，如果一个集合不包含任何元素，它可以用$\{\}$ 来表示，基于列举法，或者可以用$\varnothing$来表示。这种集合被称为空集。

另一种描述集合的方法是使用文字。例如，考虑集合$S$，它包含小于 10 的所有素数。如果我们使用列举法，集合$S$ 可以表示为$\{2,3,5,7\}$。

第三种描述集合的方法在集合包含许多元素时很有优势。这种方法被称为集合构建器符号。在这种符号中，花括号内有三个部分。它们在下面用描述说明：$$\underbrace {\{} _{\text{The set of}}\underbrace {x} _{{\text{all elements }}x}\underbrace {:} _{\text{such that}}\underbrace {P(x)} _{{\text{the property }}P(x){\text{ is satisfied}}}\}$$

正如预期的那样，两个集合相等当且仅当它们包含相同的元素。等价地，两个集合$A$和$B$相等当且仅当$A$的每个元素也是$B$的元素，$B$的每个元素也是$A$的元素。这可以被看作一个公理或一个定义。如果两个集合$A$和$B$相等，我们写$A=B$。如果不是，我们写$A\neq B$.

在这本书中，当我们求解一个方程时，我们只考虑它的实数解，除非另有说明。

例子。

• $\{x:3x+2=0\}=\{-2/3\}$.
• $\{y:y{\text{ is a positive odd number}}\}=\{1,3,5,\ldots \}$.
• $\{z:z{\text{ is an English letter}}\}=\{a,b,c,\ldots ,z,A,B,\ldots ,Z\}$.

练习。 假设$a$和$b$是不同的元素。以下每个陈述是真还是假？

1 集合${\big \{}\{\}{\big \}}$不包含任何元素。

	正确。
	错误。

2 $\{\}=\varnothing .$

	正确。
	错误。

3 $\{1,1,2,3\}$是一个集合。

	正确。
	错误。

4 $\{x:0<x<2{\text{ and }}x^{2}=4\}=\{2\}$.

	正确。
	错误。

5 $\{a,b,b\}\in \{\{a,b\},a,b,b\}$.

	正确。
	错误。

6 $\{\{a\},\{a\}\}\in \{\varnothing ,\{a\},\{b\},\{a,b\}\}$.

	正确。
	错误。

集合基数

如果一个集合包含 有限 个元素，则称为 有限 集合，否则称为 无限 集合。 如果一个集合是有限的，那么它的基数就是它的元素个数。 对于无限集，定义它们的基数比较困难和复杂，所以我们将在后面的关于集合基数的章节中进行讨论。 对于每个集合 $S$，它的基数用 $|S|$ 表示。

例子。

• 令 $A=\{{\text{red}},{\text{yellow}},{\text{blue}}\}$。 那么，$|A|=3$.
• 令 $B=\{\varnothing ,\{\varnothing \},\varnothing \}$。 那么，$|B|=2$（不是 3，因为元素 $\varnothing$ 重复列出了）。
• 令 $C=\{x:x^{2}<0\}$。 那么，$|C|=0$，因为 $x^{2}<0$ 没有解（对于实数 $x$），因此 $C$ 是一个空集。
• 令 $D=\{y:y^{2}-4y+4=0\}$。求解 $y^{2}-4y+4=0\Leftrightarrow (y-2)^{2}=0$，得到 $y=2$。因此，$D=\{2\}$，因此 $|D|=1$ .

有一些特殊的无限集，它们的记号如下所示

• $\mathbb {N}$ 是所有自然数的集合（在本教材中，不 将 0 视为自然数）。
• $\mathbb {Z}$ 是所有整数的集合。
• $\mathbb {Q}$ 是所有有理数的集合。
• （非标准记号）$\mathbb {I}$ 是所有无理数的集合。
• $\mathbb {R}$ 是所有实数的集合。
• $\mathbb {C}$ 是所有复数的集合。

特别地，我们可以使用集合生成式来表示 $\mathbb {Q}$，如下所示：$\mathbb {Q} =\{p/q:p,q\in \mathbb {Z} {\text{ and }}q\neq 0\}$.

例子。

• ${\sqrt {2}},{\sqrt {3}}\notin \mathbb {Q}$
• ${\sqrt {5}},\pi ,e\in \mathbb {I}$

练习。 使用集合生成式来表示 $\mathbb {C}$，不使用 "$\mathbb {C}$" 在表达式中。

解答

我们可以这样表示：$\mathbb {C} =\{x:x=a+bi{\text{ and }}a,b\in \mathbb {R} \}$ ($i={\sqrt {-1}}$).

子集

定义. (子集) 集合 $A$ 是集合 $B$ 的 子集 (记为 $A\subseteq B$)，如果 $A$ 中的每个元素也是 $B$ 的一个元素。

备注。

• 如果 $A$ 不是 $B$ 的子集，我们将其记为 $A\not \subseteq B$。
• 回想一下，两个集合 $A$ 和 $B$ 相等，当且仅当 $A$ 中的每个元素都属于 $B$，并且 $B$ 中的每个元素都属于 $A$。利用子集的概念，我们可以写出 $A=B$，当且仅当 $A\subseteq B$ 并且 $B\subseteq A$。

例子。

• $\mathbb {N} \subseteq \mathbb {Z} \subseteq \mathbb {Q} \subseteq \mathbb {R} \subseteq \mathbb {C}$.
• $\mathbb {Z} \not \subseteq \mathbb {I}$ (例如，$1\in \mathbb {Z}$ 但 $1\notin \mathbb {I}$)
• $\mathbb {C} \not \subseteq \mathbb {R}$ (例如，$i\in \mathbb {C}$ 但 $i\notin \mathbb {R}$)
• 对于每个集合 $S$，$S\subseteq S$，即每个集合都是它自身的子集。

• 这是因为集合 $S$ 的每个元素都是 $S$ 的元素。

• 对于每个集合 $S$，$\varnothing \subseteq S$。

• 如果我们想直接证明这一点，会遇到一些困难，因为 $\varnothing$ 不包含任何元素。那么，“$\varnothing$ 的每个元素”是什么意思？
• 在这种情况下，最好用 反证法（一种在后面关于证明方法的章节中介绍的证明技巧）来证明。首先，我们假设相反，即 $\varnothing \not \subseteq S$。根据定义的否定，存在 至少一个 $\varnothing$ 的元素，它 不是 $S$ 的元素，这是错误的。这产生了矛盾，因此假设是错误的（稍后会解释），即 $\varnothing \not \subseteq S$ 是错误的。

定义. (真子集) 如果集合 $A$ 是集合 $B$ 的 真子集 (记作 $A\subsetneq B$)，则 $A$ 是 $B$ 的子集，并且 $A\neq B$.

备注。

• 类似地，如果 $A$ 不是 $B$ 的真子集，我们写成 $A\not \subsetneq B$.

例子。

• 对于每个 非空 集合 $S$，$\varnothing \subsetneq S$，因为 $\varnothing \subseteq S$ (前面已经证明) 并且 $\varnothing \neq S$ 如果 $S$ 是一个 非空 集合。
• $\mathbb {N} \subsetneq \mathbb {Z} \subsetneq \mathbb {Q} \subsetneq \mathbb {R} \subsetneq \mathbb {C}$.
• $\{1,2\}\subsetneq \{1,2,3\}$.
• $\{1,2\}\not \subsetneq \{\{1,2\},2,3\}$ 并且 $\{1,2\}\not \subseteq \{\{1,2\},2,3\}$.

练习。 令 $A=\{1\}$.

1 以下哪些集合是 $A$ 的子集？

	$\{1\}$
	$\{\}$
	$\{\{1\}\}$
	$\{1,\{1\}\}$

2 选择哪些集合是 $A$ 的超集？

	$\{1\}$
	$\{\}$
	$\{\{1\}\}$
	$\{1,\{1\}\}$

3 选择哪些集合是 $A$ 的元素？

	$\{1\}$
	$\{\}$
	$\{\{1\}\}$
	$\{1,\{1\}\}$

我们把一些常见的 $\mathbb {R}$ 的子集称为 区间。对于每个实数 $a,b$，满足 $a<b$，

• $(a,b){\overset {\text{ def }}{=}}\{x\in \mathbb {R} :a<x<b\}$ （开区间）
• $(a,b]{\overset {\text{ def }}{=}}\{x\in \mathbb {R} :a<x\leq b\}$ （半开（或半闭）区间）
• $[a,b){\overset {\text{ def }}{=}}\{x\in \mathbb {R} :a\leq x<b\}$ （半开（或半闭）区间）
• $[a,b]{\overset {\text{ def }}{=}}\{x\in \mathbb {R} :a\leq x\leq b\}$ （闭区间）

也有一些 无限 区间

• $(-\infty ,a){\overset {\text{ def }}{=}}\{x\in \mathbb {R} :x<a\}$
• $(-\infty ,a]{\overset {\text{ def }}{=}}\{x\in \mathbb {R} :x\leq a\}$
• $(a,\infty ){\overset {\text{ def }}{=}}\{x\in \mathbb {R} :a<x\}$
• $[a,\infty ){\overset {\text{ def }}{=}}\{x\in \mathbb {R} :a\leq x\}$
• $(-\infty ,\infty ){\overset {\text{ def }}{=}}\mathbb {R}$

注意：$\{x\in S:P(x)\}$ 是 $\{x:x\in S{\text{ and }}P(x)\}$ 的简写形式 ($S$ 是一个集合)。

例子。

• $(0,1)\subseteq [0,1)\subseteq [0,1]$.
• ${\sqrt {2}},e,\pi \in (1,4)$.
• $(0,1]\not \subseteq [0,1)$ 因为左侧集合中的元素 "1" 不 属于右侧集合。
• $(0,1)\subseteq (0,\infty )$.

例子。

• $x^{2}-9\leq 0$ 的 (实数) 解集是 $[-3,3]$.
• $x^{2}\leq 0$ 的 (实数) 解集是 $\{0\}$。(注意：我们不能 用 $[0,0]$ 来表示这个集合，因为要求对于区间 $[a,b]$，$a<b$）。
• 方程 $x^{2}<0$ 的（实数）解集是 $\varnothing$.

练习。

以下哪些是有效的区间？

	$(0,0)$
	$(0,0.000001)$
	$(-2,-3)$
	$[-1,\infty ]$

全集和韦恩图

定义。（全集）全集，用 $U$ 表示，是一个包含特定研究中所有元素的集合。

例子。

• 如果我们研究的是实数，那么全集就是 $\mathbb {R}$.

定义。（补集）集合 $A$ （它是全集 $U$ 的子集）的 补集，用 $A^{c}$ 表示，是集合 $\{x\in U:x\notin A\}$.

例子。

• 令 $A=\{1\}$ 且 $U=\{0,1,1,2\}$。那么，$A^{c}=\{0,2\}$。（注意：$U=\{0,1,2\}$ 也是。）
• 对于每个全集 $U$，$\varnothing ^{c}=U$（因为 $U$ 中的每个元素都不属于 $\varnothing$）并且 $U^{c}=\varnothing$（因为 $U$ 中没有元素不属于 $U$）。
• 令 $B=\{1,3,5\}$ 并且 $U=\{2,4,6\}$。那么，$B^{c}=\{2,4,6\}=U$，因为 $U$ 中的每个元素都不属于 $B$。

练习。 令全集为 $\mathbb {R}$。

1 什么是 $(-\infty ,1]^{c}$?

	$[1,\infty )$
	$(1,\infty )$
	$(-\infty ,1)$
	$(-\infty ,1]$

2 什么是 $(-\infty ,1)^{c}$?

	$[1,\infty )$
	$(1,\infty )$
	$(-\infty ,1)$
	$(-\infty ,1]$

3 如果全集是 $U$，$(-\infty ,1)^{c}=(1,3)$。以下哪些可以是 $U$（可能不止一个答案）？

	$[1,3]$
	$(1,3)$
	$(1,\infty )$
	$(3,\infty )$
	$(-\infty ,3)$

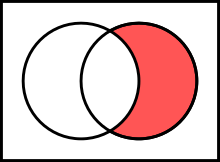
一个 维恩图 是一个图，它显示了有限个集合之间所有可能的逻辑关系。全集通常用矩形围成的区域表示，而集合通常用圆形围成的区域表示。以下是一个维恩图。

在这个图中，如果白色区域表示集合 $A$，矩形围成的区域表示全集，那么红色区域就是集合 $A^{c}$。

然而，以下 不是 维恩图。

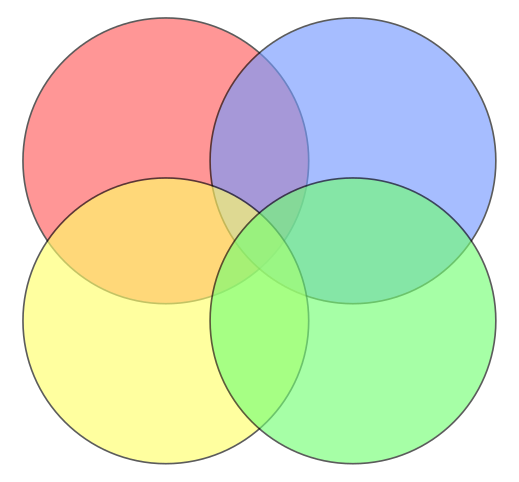
这是因为没有区域只有黄色和蓝色区域相交，只有红色和绿色区域相交。所以，不是 所有 集合之间的逻辑关系都显示出来了。

为了显示四个集合之间所有逻辑关系，可以使用以下维恩图。

集合运算

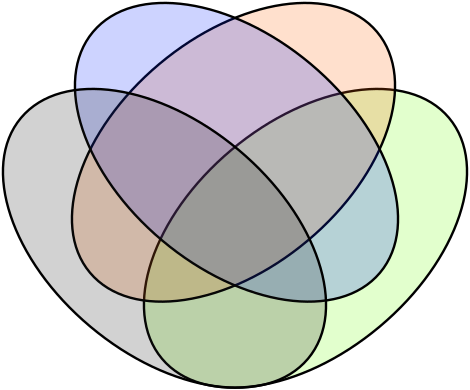
类似于将两个实数组合成一个的算术运算，集合运算将两个集合组合成一个。

集合的并集

定义. (集合的并集)

两个集合的并集的维恩图。

集合 $A$ 和集合 $B$ 的 并集，记为 $A\cup B$，是集合 $\{x:x\in A{\text{ or }}x\in B\}$。

备注。

• 这里的“或”是 包含的，即如果一个元素属于 两个 $A$ 和 $B$，它也属于 $A\cup B$。

例子。

• $\{1,3,5\}\cup \{2,4,6\}=\{1,2,3,4,5,6\}$.
• $\{1,3,5\}\cup \{1,4,6\}=\{1,3,4,5,6\}$.
• $\{1,3,5\}\cup \{1,3,5\}=\{1,3,5\}$.
• $\mathbb {Q} \cup \mathbb {I} =\mathbb {R}$.

命题. 令 $A,B$ 和 $C$ 为集合. 那么,

• $A\cup A=A$
• $A\cup B=B\cup A$ (交换律)
• $A\cup (B\cup C)=(A\cup B)\cup C$ (结合律)
• $A\subseteq A\cup B$ 以及 $B\subseteq A\cup B$
• $A\cup \varnothing =A$

证明. (形式)证明将在稍后讨论. 现在, 你可以使用维恩图来验证这些结果.

$\Box$

备注。

• 由于结合律, 我们可以写三个 (或更多) 集合的并集而不需要括号. 交集的集合将有类似的结果, 所以我们也可以写三个 (或更多) 集合的交集而不需要括号.

集合的交集

定义. (集合的交集)

两个集合交集的维恩图.

集合 $A$ 和集合 $B$ 的 交集, 记为 $A\cap B$, 是集合 $\{x:x\in A{\text{ and }}x\in B\}$.

备注。

• 如果 $A\cap B=\varnothing$, 我们说 $A$ 和 $B$ 是 不相交 的.

命题. 令 $A,B$ 和 $C$ 为集合. 那么,

• $A\cap A=A$
• $A\cap B=B\cap A$ (交换律)
• $A\cap (B\cap C)=(A\cap B)\cap C$ （结合律）
• $A\cap B\subseteq A$ 和 $A\cap B\subseteq B$
• $A\cap \varnothing =A$

证明. (形式)证明将在稍后讨论. 现在, 你可以使用维恩图来验证这些结果.

$\Box$

命题。 （分配律）令 $A,B$ 和 $C$ 为集合。那么，

• $A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$ （“$A\cap$” 分布到 $B$ 和 $C$ 分别）
• $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

相对补集

定义。 （相对补集）

相对补集的文氏图。如果左圆和右圆所包围的区域分别代表 $A$ 和 $B$，那么红色区域代表 $B\setminus A$。

集合 $A$ 在集合 $B$ 中的 相对补集，记作 $B\setminus A$，是集合 $\{x:x\in B{\text{ and }}x\notin A\}$。

备注。

• $A^{c}=U\setminus A$ 如果 $U$ 是全集。因此，集合 $A$ 的补集也是 $A$ 在 $U$ 中的相对补集。
• 符号 $B\setminus A$ 读作“去掉 A 后剩下的 B”。
• 从定义可以看出 $B\setminus A=B\cap A^{c}$

例子。

• $\{a,b,c\}\setminus \{b,c,d\}=\{a\}$.
• $\{a,b,c\}\setminus \{a,b,c,d\}=\varnothing$.
• $\{a,b,c\}\setminus \{1,2,3\}=\{a,b,c\}$.
• $\mathbb {R} \setminus \mathbb {Q} =\mathbb {I}$.
• $\mathbb {Z} \setminus \mathbb {N} =\{0,-1,-2,\ldots \}$.

练习。

1 什么是 $\mathbb {R} \setminus \mathbb {C}$？

	$\{x:x=a+bi,a,b\in \mathbb {R} {\text{ and }}b\neq 0\}$
	$\{x:x=bi,b\in \mathbb {R} \}$
	$\varnothing$
	$\mathbb {C}$
	$\mathbb {R}$

2 什么是 $[1,10]\setminus (3,5)$?

	$[1,3]\cup [5,10]$
	$[1,3)\cup (5,10]$
	$(1,3)\cup (5,10)$
	$(1,3]\cup [5,10)$

3 什么是 $\mathbb {R} \setminus \{0\}$?

	$(-\infty ,0)\cup (0,\infty )$
	$(-\infty ,0]\cup [0,\infty )$
	$(-\infty ,0)\cap (0,\infty )$
	$(-\infty ,0]\cap [0,\infty )$

4 以下哪个/哪些集合表示所有正数的集合？

	$\mathbb {R} \setminus (-\infty ,0)$
	$\mathbb {R} \setminus (-\infty ,0]$
	$(0,\infty )$
	$[0,\infty )$
	$\mathbb {R} \cup (0,\infty )$
	$\mathbb {R} \cap (0,\infty )$

5 什么是 $\varnothing \setminus \varnothing$?

	$\varnothing$
	全集。
	$\{\varnothing \}$

命题。 令 $A$ 和 $B$ 为集合。那么，

• $A\setminus A=\varnothing$.
• $A\setminus \varnothing =A$.
• $\varnothing \setminus A=\varnothing$.
• $A\setminus B=\varnothing$ 当且仅当 $A\subseteq B$.
• $(A\setminus B)\cap (B\setminus A)=\varnothing$.
• $A\cap (B\setminus A)=\varnothing$.

证明. (形式)证明将在稍后讨论. 现在, 你可以使用维恩图来验证这些结果.

$\Box$

定理。 (德摩根定律) 令 $A$ 和 $B$ 为集合。那么，$$(A\cup B)^{c}=A^{c}\cap B^{c}{\text{ and }}(A\cap B)^{c}=A^{c}\cup B^{c}.$$

证明. (形式)证明将在稍后讨论. 现在, 你可以使用维恩图来验证这些结果.

$\Box$

示例。 假设全集是 $\{1,2,3,4,5,6,7\}$，$A=\{1,2,3\}$ 并且 $B=\{1,3,5\}$。由于 $A\cup B=\{1,2,3,5\}$，$(A\cup B)^{c}=\{4,6,7\}$。另一方面，由于 $A^{c}=\{4,5,6,7\}$ 并且 $B^{c}=\{2,4,6,7\}$，$A^{c}\cap B^{c}=\{4,6,7\}=(A\cup B)^{c}$.

练习。

什么是 $(A\cap B)^{c}$？

	$\{4,6,7\}$
	$\{4,5,6,7\}$
	$\{2,4,6,7\}$
	$\{2,4,5,6,7\}$

对称差

定义。 （对称差）

一个用于说明对称差的韦恩图。

集合 $A$ 和 $B$ 的 对称差，记作 $A\triangle B$，是集合 $(A\setminus B)\cup (B\setminus A)$.

例子。

• $\{0,1,2\}\triangle \{1,2,3\}=\{0\}\cup \{3\}=\{0,3\}$.
• $\{x,y\}\triangle \{y\}=\{x\}\cup \varnothing =\{x\}$
• $\{x\}\triangle \{y\}=\{x\}\cup \{y\}=\{x,y\}$

命题. 令 $A,B$ 和 $C$ 为集合. 那么,

• $A\triangle A=\varnothing$
• $A\triangle \varnothing =A$
• $A\triangle B=(A\cup B)\setminus (A\cap B)$
• $A\triangle (B\triangle C)=(A\triangle B)\triangle C$ (结合律)
• $A\triangle B=B\triangle A$ (交换律)

练习。

1 $\varnothing \triangle \varnothing$ 等于什么？

	$\varnothing$
	$\{\varnothing \}$
	$\{\varnothing ,\{\varnothing \}\}$
	$\{\{\varnothing \}\}$

2 $A\triangle (B\setminus A)$ 等于什么？

	$A\cup B$
	$A\cap B$
	$A\setminus B$
	$A\triangle B$
	$B\setminus A$
	$A$
	$B$

3 $A\triangle B\triangle C=(A\cup B\cup C)\setminus (A\cap B\cap C)$ (试着利用韦恩图来确定，目前不需要数学证明。)

	是。
	否。

幂集

定义。 （幂集）集合 $A$ 的幂集，记作 ${\mathcal {P}}(A)$，是 $A$ 的所有子集的集合。用集合生成式表示，${\mathcal {P}}(A)=\{S:S\subseteq A\}$。

备注。

• 因为 $\varnothing \subseteq A$ 对于每个集合 $A$ 成立，$\varnothing$ 是每个幂集的元素。
• 同样，因为 $A\subseteq A$ 对于每个集合 $A$ 成立，$A$ 是幂集 ${\mathcal {P}}(A)$ 的元素。

例子。

• ${\mathcal {P}}(\varnothing )=\{\varnothing \}$。它的基数是 1。
• 如果 $A=\{1\}$，那么 ${\mathcal {P}}(A)=\{\varnothing ,A\}=\{\varnothing ,\{1\}\}$。它的基数是 2。
• 如果 $B=\{1,\{1\}\}$，那么 ${\mathcal {P}}(B)=\{\varnothing ,\{1\},\{\{1\}\},B\}$。它的基数是 4。
• ${\mathcal {P}}(\{1,2,3\})=\{\varnothing ,\{1\},\{2\},\{3\},\{1,2\},\{2,3\},\{1,3\},\{1,2,3\}\}$. 它的大小是 8。

定理。 (有限集幂集的大小) 设 $A$ 是一个大小为 $n$ 的有限集。那么， $|{\mathcal {P}}(A)|=2^{n}$.

证明。 假设 $A$ 是一个大小为 $n$ 的有限集。由于幂集 ${\mathcal {P}}(A)$ 的每个元素都是 $A$ 的子集，所以只需要证明 $A$ 有 $2^{n}$ 个子集。下面，我们分别考虑 $A$ 中元素个数不同的子集，并使用组合学计算每种不同类型子集的个数。

• 对于元素个数为零的子集，它就是空集，所以只有一个这样的子集。
• 对于元素个数为一的子集，有 $C_{1}^{n}$ 个子集。
• 对于元素个数为二的子集，有 $C_{2}^{n}$ 个子集。
• ...
• 对于元素个数为 $n-1$ 的子集，有 $C_{n-1}^{n}$ 个子集。
• 对于包含 $n$ 个元素的子集，它是集合 $A$，因此只有一个这样的子集。

因此，集合 $A$ 的子集总数为 $1+C_{1}^{n}+C_{2}^{n}+\dotsb +C_{n-1}^{n}+1=(1+1)^{n}=2^{n}$，根据 二项式定理。

$\Box$

备注。

• 这里采用的证明方法称为 直接证明，这可能是最“自然”的方法，也是最常用的方法。我们将在 后面章节 中讨论证明方法。
• 有其他方法可以证明这个定理。

练习。 在下列问题中，选择给定集合的 幂集。

1 $\{\varnothing \}$

	${\big \{}\varnothing ,\{\{\varnothing \}\}{\big \}}$
	${\big \{}\{\varnothing \},\{\{\varnothing \}\}{\big \}}$
	${\big \{}\varnothing ,\{\varnothing \}{\big \}}$
	${\big \{}\varnothing ,\{\varnothing \},\{\{\varnothing \}\}{\big \}}$

2 ${\mathcal {P}}(\{\varnothing \})$

	${\big \{}\varnothing ,\{\varnothing \},\{\{\varnothing \}\},\{\varnothing ,\{\varnothing \}\}{\big \}}$
	${\big \{}\varnothing ,\{\varnothing ,\{\varnothing \}\},\{\{\varnothing \}\},\{\varnothing ,\{\varnothing \}\}{\big \}}$
	$\left\{\varnothing ,\{\{\varnothing \}\},\{\{\{\varnothing \}\}\},{\big \{}\{\varnothing \},\{\{\varnothing \}\}{\big \}}\right\}$
	$\left\{\varnothing ,\{\varnothing \},\{\{\varnothing \}\},{\big \{}\{\varnothing \},\{\{\varnothing \}\}{\big \}}\right\}$

3 $\{a,\{a\}\}$

	$\{\varnothing ,\{a\},\{\{a\}\},\{a,\{a\}\}\}$
	$\{\varnothing ,a,\{\{a\}\},\{a,\{a\}\}\}$
	$\{\varnothing ,a,\{a\},\{\{a\}\}\}$

4 $S=\{1,3\}\triangle \{3,5\}$

	$\{\varnothing ,\{1\},\{3\},\{5\},\{1,3\},\{3,5\},\{1,5\},S\}$
	$\{\varnothing ,\{1\},\{3\},\{5\},S\}$
	$\{\varnothing ,S\}$
	$\{\varnothing ,\{1\},\{5\},\{1,5\},S\}$

已知 $|A|=2$。在以下每个问题中，选择题目中给定集合的 基数。

1 ${\mathcal {P}}({\mathcal {P}}(A))$

	4
	8
	16
	32

2 ${\mathcal {P}}({\mathcal {P}}(\varnothing ))$

	0
	1
	2
	4

3 $\{{\mathcal {P}}(A)\}$

	1
	2
	4
	8

4 ${\mathcal {P}}(\{A\})$

	1
	2
	4
	8

5 ${\mathcal {P}}(\varnothing \cap {\mathcal {P}}(A))$

	1
	2
	4
	8

笛卡尔积

定义。 (笛卡尔积) 集合 $A$ 和 $B$ 的 笛卡尔积，记作 $A\times B$，是 $A\times B=\{(a,b):a\in A{\text{ and }}b\in B\}$.

备注。

• $(a,b)$ 是一个 有序对（即顺序 重要 的一对事物）。

• 有序对用于指定平面上的点，有序对称为 坐标。

• 特别地，我们有 $(a,b)\neq (b,a)$ 如果 $a\neq b$.
• (符号) 我们使用 $A^{2}$ 表示每个集合 $A$ 的 $A\times A$。
• 我们可以观察到 $|A\times B|=|A|\times |B|$。

示例. 令 $A=\{0,1\}$ 且 $B=\{a,b,c\}$。那么，

• $A\times B=\{(0,a),(0,b),(0,c),(1,a),(1,b),(1,c)\}$.
• $B\times A=\{(a,0),(b,0),(c,0),(a,1),(b,1),(c,1)\}$.

备注。

• 从上面的例子可以看出，笛卡尔积是 非交换的，即 $A\times B=B\times A$ 不一定成立。

练习. 令 $A=\{1,2,3\}$。

1 什么是 $A\times \varnothing$（可能有多个答案）？

	$\{(1,0),(2,0),(3,0)\}$
	$\{(1,\varnothing ),(2,\varnothing ),(3,\varnothing )\}$
	$\varnothing$
	$\varnothing \times A$
	$\varnothing ^{2}$

2 什么是 $A^{2}$？

	$\{(1,1),(2,2),(3,3)\}$
	$\{(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)\}$
	$A$
	$\{(1,A),(2,A),(3,A)\}$

类似地，我们可以定义三个或更多集合的笛卡尔积。

定义。 (三个或更多集合的笛卡尔积) 令 $n$ 是大于 2 的整数。 $n$ 个集合 $A_{1},A_{2},\dotsc ,A_{n}$ 的笛卡尔积是 $A_{1}\times A_{2}\times \dotsb \times A_{n}=\{(a_{1},a_{2},\dotsc ,a_{n}):a_{1}\in A_{1},a_{2}\in A_{2},\dotsc ,{\text{ and }}a_{n}\in A_{n}\}$.

备注。

• (符号) 我们使用 $A^{n}$ 来表示 $\underbrace {A\times A\times \dotsb \times A} _{n{\text{ times}}}$，其中 $n\in \mathbb {N}$.