化学/三角学数学

三角学 - 正弦和余弦规则

三角形

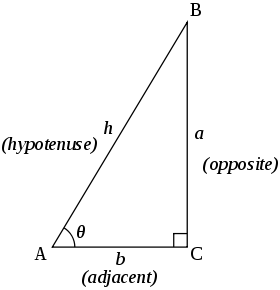
在以下三角恒等式中，$a$，$b$ 和 $c$ 是三角形中对应角 $A$，$B$ 和 $C$ 对边的长度。

• 正弦定理 ${\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}$
• 余弦定理 $c^{2}=a^{2}+b^{2}-2ab\cos C$
• 比率恒等式 $\tan A={\frac {\sin A}{\cos A}}$

三角恒等式

$\cos ^{2}\theta +\sin ^{2}\theta =1$

请记住，这是毕达哥拉斯定理的结果，其中斜边的长度为 1。

$\sin(\theta +\phi )=\sin \theta \cos \phi +\cos \theta \sin \phi$

$\cos(\theta +\phi )=\cos \theta \cos \phi -\sin \theta \sin \phi$

两个角度的差可以通过将 $\phi =-\phi$代入并记住 $\sin -\phi =-\sin \phi$ 和 $\cos -\phi =\cos \phi$来轻松生成。类似地，倍角公式可以通过归纳法生成。 $\tan(\theta +\phi )$稍微复杂一些，但如果你能处理分数，就可以生成它！证明过程可以在许多教科书中找到，但作为化学家，没有必要知道它们，只需要知道结果即可。

恒等式和方程

恒等式和方程看起来非常相似，都是由一个等号连接的两个事物。然而，恒等式是数学等价性的记忆辅助工具，可以被证明。方程代表关于某个情况的新信息，可以被求解。

例如，

$\cos ^{2}\theta +\sin ^{2}\theta =1$

是一个恒等式。它不能被求解 $\theta$；它对所有 $\theta$ 都成立。然而，

$\cos ^{2}\theta =1$

是一个方程，其中 $\theta =\arccos \pm 1$.

如果你尝试将一个恒等式作为方程求解，你会陷入循环，毫无进展，但你可以将 $\cos ^{2}\theta +\sin ^{2}\theta =1$ 转换成一个非常复杂的表达式，你可能会把它误认为是一个方程。

关于三角形的几个观察

检查你是否熟悉基本的几何知识。从你的 GCSE 数学中记住等边三角形和等腰三角形的性质。如果你有一个等腰三角形，你总是可以省略正弦定理和余弦定理，从底边垂下一条垂直线，直接使用三角函数。记住，一条边或一个角到顶点的角平分线将三角形按面积、角度和长度分成两部分。这可以通过画一个钝角三角形来证明，可以看到面积是 ${\frac {1}{2}}{\frac {1}{2}}.R.h$.

多边形的内角

记住，一个 $n$ 边形的内角是 $180(n-2)$（以度为单位）或 ($n\pi -2\pi$)（以弧度为单位）。

对于 苯，如果将环的中心用作顶点，则有六个等边三角形，每个三角形的内角为 120 度。假设所有 C-C 键长相等（这只是一个近似值），计算薁（一种具有五元环和七元环的烃）的角。