纳米技术/半导体纳米结构

导航
<< 上一页：生产方法概述
>< 主页：纳米技术
>> 下一页：金属纳米结构

---

纳米管

某些化合物能够形成纳米管，其中管由圆形外壳组成，外壳由单个原子层在圆柱形晶格中组成。碳纳米管是最著名的例子，但其他材料也可以形成纳米管，例如氮化硼、二硫化钼等。

纳米管也可以通过蚀刻掉壳结构棒的芯来制造，但这样的管通常会在壁中包含许多原子层，并在侧面具有晶面。

碳纳米管

碳纳米管是迷人的纳米结构。石墨中常见的一张石墨烯薄片，但卷成小管而不是平面薄片。

碳纳米管具有独特的机械性能，如高强度、高刚度和低密度，以及有趣的电子性能。单壁碳纳米管可以是金属或半导体，具体取决于原子排列。

本节简要介绍了碳纳米管。有关更广泛的概述，请读者参考大量有关碳纳米管的评论文章或书籍。

几何结构

最简单的碳纳米管类型仅由一层石墨烯组成，卷成无缝圆柱体，被称为单壁碳纳米管 (SWCNT)，其典型直径仅为几个纳米。更大的直径纳米管结构是纳米管绳，由许多独立的平行纳米管组成，紧密排列成六角形晶格，以及多壁碳纳米管 (MWCNT)，由彼此嵌套的几个同心圆柱体组成。

由使用含铁催化粒子的 CVD 工艺制成的多壁碳纳米管 (MWCNT) 样品。MWCNT 粘附在垫子上。

单壁碳纳米管

因此，基本配置是 SWCNT。它的结构最容易被解释为一个圆柱形管，概念上由单个石墨烯片卷曲而成。二维石墨烯片的六角形结构是由于碳原子的$sp^{2}$ 杂化引起的，该杂化导致三个方向上的平面内$\sigma$ 键，这些键之间的夹角为 120 度。

纳米管可以通过手性矢量$C$ 来描述，该矢量可以用石墨烯单位矢量${\textbf {a}}_{1}$ 和${\textbf {a}}_{2}$ 表示，如${\textbf {C}}=n{\textbf {a}}_{1}+m{\textbf {a}}_{2}$，其中整数集$(n,m)$ 唯一地标识了纳米管。此手性矢量或“卷起”矢量通过连接两个晶体学等效位置来描述纳米管周长，即该管通过叠加${\textbf {C}}$ 的两端而形成。

根据手性角，单壁碳纳米管被定义为锯齿形管 ($\theta =0deg\leftrightarrow m=0$), 扶手椅形管 ($\theta =30deg\leftrightarrow n=m$), 或手性管 ($0deg<\theta <30deg$).

多壁碳纳米管

MWCNTs 由多个 SWCNTs 组成，它们以同轴几何形状排列。每个嵌套壳体的直径为 $d={\sqrt {3}}a_{C-C}(m^{2}+n^{2}+mn)^{1/2}/\pi$，其中 $a_{C-C}$ 是碳-碳键的长度，为 1.42 Å。各个壳体直径的差异意味着它们的手性不同，因此相邻壳体通常不共面，这导致壳间相互作用很弱。

MWCNTs 中的壳间间距为 $\sim$ 0.34 nm - 与乱层石墨中的层间间距非常接近

电子结构

SWCNT 的电子结构最容易通过再次考虑单层石墨烯片来描述。二维、六边形晶格石墨烯片具有二维倒空间和六边形布里渊区 (BZ)。

该 $\sigma$ 键主要负责机械性能，而电子性能主要由 $\pi$ 带决定。通过紧束缚方法，可以计算这些 $\pi$ 带的能带结构

石墨烯是一种零带隙半导体，它有一个被占据的 $\pi$ 带和一个未被占据的 $\pi ^{*}$ 带，它们在 BZ 中的六个 $K$ 点处相遇，因此表现出金属特性，即所谓的半金属。

通过将石墨烯片概念性地卷起来形成纳米管，施加一个周期性边界条件，这使得只有平面石墨烯片中某些电子态被允许。这些态由纳米管的几何结构决定，即由手性向量的索引 $(n,m)$ 决定。允许状态的波矢量落在线性空间中石墨烯 BZ 中的特定直线上。

基于这种方案，可以估计特定的纳米管是金属的还是半导体的。当允许的状态包括 $K$ 点时，系统将近似表现为金属。然而，在 $\pi$ 和 $\pi ^{*}$ 能带相遇，但由于曲率效应略微偏离 $K$ 点，在某些情况下会导致能带略微打开

这导致了纳米管分类方案，共有三种类型：

• 金属：这些是扶手椅型纳米管，其中简并点的微小偏移远离 $K$ 点不会因对称性原因导致能带打开。

• 小带隙半导体：这些的特征是 $n-m=3j$，其中 $j$ 是一个整数。这里，允许状态的波矢穿过 $K$ 点，但由于简并点的微小偏移，会存在一个小的能隙，其大小与纳米管直径的平方成反比，典型值为几毫电子伏到几十毫电子伏之间。

• 半导体：在这种情况下 $n-m\neq 3j$。这会导致更大的能隙，其大小与纳米管直径成反比： $E_{g}=k/d$，实验研究表明 $k$ 为 0.7-0.8 eV/nm。

通常，类型 2 纳米管的能隙非常小，以至于它们在室温下可以被认为是金属的。据此可以推断，所有纳米管的 1/3 应该表现出金属特性，而剩下的 2/3 应该表现出半导体特性。然而，需要注意的是，由于半导体纳米管的能隙与直径成反比，因此大直径纳米管在室温下往往会表现出金属特性。这在大型 MWCNTs 中尤为重要。

从电学角度来看，MWCNT 可以被视为许多仅弱相互作用的平行导体的复杂结构。由于探测电学性质通常涉及电极接触最外层壳，因此该壳将主导传输性质 。简单来说，这可以与大直径 SWCNT 相比，因此通常会表现出金属行为。

电学和机电性质

许多研究都集中在 SWCNTs 上，以探索纳米管的基本性质。由于其本质上的一维性质和有趣的电子结构，SWCNTs 在低温下表现出一系列有趣的量子现象

然而，这里讨论的内容目前主要限于室温性质。

一维导体（如 SWCNT）的电导率 $~G~$ 由朗道尔公式给出

$~G=G_{0}\sum _{i}T_{i}~$,

其中 $~G_{0}=2e^{2}/h=(12.9{\rm {k\Omega )^{-1}}}$；
$~1/G_{0}~$ 是电导量子；
以及 $~T_{i}~$ 是贡献通道 $~i~$ 的透射系数。

关于纳米管的更多信息

• 维基百科 碳纳米管
• 纳米管网站
• 碳纳米管属性的汇总概述

碳纳米管及相关产品的商业供应商

• Nanoledge.com 纳米管及相关产品 - 纤维、颗粒、树脂和分散体...
• Carbon Solution, Inc. 主要为单壁碳纳米管。
• BuckyUSA 富勒烯、单壁碳纳米管、多壁碳纳米管。
• CNI HiPco 碳纳米管
• Carbolex 单壁碳纳米管，亚克级通过西格玛奥德里奇销售
• 西格玛奥德里奇 单壁碳纳米管

"足球烯"

C₆₀，利用 DFT 计算出的基态电子密度的等值面。

一个 w:足球 是巴克明斯特富勒烯 C₆₀ 的模型。

巴克明斯特富勒烯 (IUPAC 名称 (C₆₀-I_h)[5,6]富勒烯) 是最小的富勒烯分子，其中没有两个五元环共享边（这可能导致不稳定，如 戊搭烯）。它也是自然界中最常见的，因为它经常存在于 煤烟 中。

C₆₀ 的结构是 截角（T = 3）二十面体，类似于 足球，由 20 个六元环和 12 个五元环组成，每个多边形的顶点处有一个碳原子，每个多边形的边上有一条键。

C₆₀ 分子的 w:范德华直径 约为 1 纳米 (nm)。C₆₀ 分子的核间距离约为 0.7 纳米。

C₆₀ 分子有两个键长。6:6 环键（两个六元环之间）可以被认为是 "双键"，并且比 6:5 键（六元环和五元环之间）短。它的平均键长为 1.4 埃。

硅足球烯已在金属离子周围形成。

硼足球烯

莱斯大学的研究人员预测并描述了一种新型的足球烯，它使用 硼 原子代替通常的碳原子。B-80 结构，每个原子形成 5 或 6 个键，预计比 C-60 足球烯更稳定。 研究人员给出的原因之一是，B-80 实际上更像巴克明斯特·富勒推广的原始测地线圆顶结构，它使用三角形而不是六边形。然而，这项工作受到了量子化学家的广泛批评，因为他们得出结论，预测的 Ih 对称结构在振动上是不稳定的，并且由此产生的笼发生自发对称性破缺，产生一个具有罕见的 Th 对称性的起伏笼（排球 的对称性）。该分子中六原子环的数量为 20，五元环的数量为 12。每个六元环中心都有一个额外的原子，与周围的每个原子相连。

足球烯的变体

另一种相当常见的巴克明斯特富勒烯是 C₇₀， 但是通常可以获得具有 72、76、84 甚至高达 100 个碳原子的富勒烯。

在 数学 术语中，富勒烯 的结构是具有五元环和六元环面的 三价 凸 多面体。在 图论 中，术语 富勒烯 指任何 3- 正则、平面图，其所有面都为 5 或 6（包括外部面）。由 欧拉多面体公式 |V|-|E|+|F| = 2，（其中 |V|、|E|、|F| 表示顶点、边和面的数量）可知，富勒烯中恰好有 12 个五元环和 |V|/2-10 个六元环。

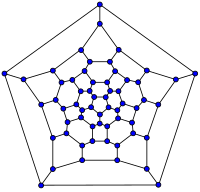
20-富勒烯 （十二面体图）	26-富勒烯图	60-富勒烯 （截角二十面体图）	70-富勒烯图

最小的富勒烯是 w:十二面体，即唯一的 C₂₀。没有 22 个顶点的富勒烯。 富勒烯 C_2n 的数量随着 n = 12、13、14... 的增加而增加，大致与 n⁹ 成正比。例如，有 1812 个非同构的富勒烯 C₆₀。注意，只有 C₆₀ 的一种形式，巴克明斯特富勒烯又名 w:截角二十面体，没有相邻的五元环（最小的这种富勒烯）。为了进一步说明这种增长，有 214,127,713 个非同构的富勒烯 C₂₀₀，其中 15,655,672 个没有相邻的五元环。

w:三金属球 碳纳米材料是由弗吉尼亚理工大学的研究人员发现的，并独家授权给 w:Luna Innovations。这类新型分子由 80 个碳原子（C80）组成一个球体，该球体包围着三个金属原子和一个氮原子的络合物。这些富勒烯封装了金属，使它们属于被称为 w:金属富勒烯 的子集。三金属球有可能用于诊断（作为安全的成像剂）、治疗和有机太阳能电池。

半导体纳米线

半导体纳米线可以用大多数半导体材料和不同的方法制成，主要是化学气相沉积过程（CVD）的各种变化。

存在许多不同的半导体材料，如果晶格常数不太不相容，则可以制成异质结构。由GaAs-GaP等材料组合制成的异质结构可用于在电气系统中制造电子屏障和导向。

低压金属有机物气相外延（MOVPE）可用于在合适的晶体衬底上外延生长III-V纳米线，例如具有相当匹配晶格常数的III-V材料或硅。

低压金属有机物气相外延（MOVPE）可用于在合适的晶体衬底上外延生长III-V纳米线，例如具有相当匹配晶格常数的III-V材料或硅。纳米线生长由各种纳米颗粒催化，这些纳米颗粒沉积在衬底表面，通常是直径为20-100nm的金纳米颗粒。

纳米线生长由各种纳米颗粒催化，这些纳米颗粒沉积在衬底表面，通常是直径为20-100nm的金纳米颗粒。

例如，要生长GaP线，通常将样品在加热的反应器室中于650℃退火，以形成金催化剂和下面的衬底之间的共晶。

然后在三甲基镓和磷化氢的前驱气体存在下，在约500℃的较低温度下进行生长。通过在生长过程中改变前驱气体，可以制成具有不同组成的纳米线异质结构

从催化金纳米颗粒生长的外延纳米线异质结构的SEM图像

资源

• 维基百科 半导体纳米线
• IOFFE 半导体物理性质

纳米颗粒

• 纳米颗粒
• 量子点

催化颗粒

• 催化剂
• 催化
• 哈伯法

纳米颗粒的商业供应商

• Reade 有各种各样的 纳米颗粒
• sigma-aldrich 有 纳米颗粒分散体
• 纳米相

贡献者和致谢

• Jakob Kjelstrup Hansen

参考文献

另请参阅有关如何添加参考文献的编辑此书籍的说明 Nanotechnology/About#How_to_contribute。

---