数值方法/误差简介

当使用数值方法或算法并使用有限精度进行计算时，会引入近似或舍入和截断误差。了解它们的性质和阶数非常重要。没有误差分析，新开发的方法就毫无价值。同样，使用引入误差幅度大于要测量或模拟的效应的方法也没有意义。另一方面，使用精度很高的方法在计算上可能过于昂贵，以至于无法证明其准确性带来的收益。

准确度和精确度

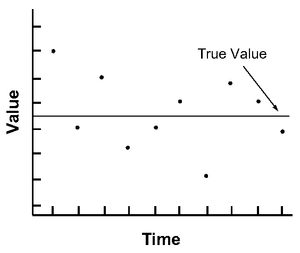
测量和计算可以根据它们的准确度和精确度来描述。准确度是指值与真值之间的一致程度。精确度是指值之间彼此一致的程度。以下图形说明了准确度和精确度之间的区别。在第一个图形中，给定值（黑点）更准确；而在第二个图形中，给定值更精确。术语“误差”表示数值计算的不精确性和不准确性。

准确度

精确度

绝对误差

绝对误差是真值 x 和近似值 xa 之间差值的幅度。因此绝对误差 = [x-xa] 两个值之间的误差定义为

$\epsilon _{abs}=\left\|x-xa\right\|\quad ,$

其中 $x$ 表示精确值，$xa$ 表示近似值。

相对误差

${\tilde {x}}$ 的相对误差是绝对误差相对于精确值的比率。从这个角度来看：如果你的测量误差为± 1 英寸，当你试图测量 3 英寸长的东西时，这似乎是一个巨大的误差。但是，当测量以英里为单位的距离时，此误差大多可以忽略不计。相对误差的定义是

$\epsilon _{rel}={\frac {\left\|{\tilde {x}}-x\right\|}{\left\|x\right\|}}\quad .$

误差来源

在数值计算中，误差可能由于以下原因而产生

• 截断误差

• 舍入误差

截断误差

“截断”一词的意思是“缩短”。截断误差是指方法中产生的误差，这种误差是由于某些数字/步骤序列（有限或无限）被截断（缩短）为更少的数字而产生的。此类误差本质上是算法误差，我们可以预测方法中将发生的误差程度。例如，如果我们通过其泰勒级数的前两个非零项来近似正弦函数，如 $\sin(x)\approx x-{\tfrac {1}{6}}x^{3}$ 对小的 $x$，则由此产生的误差就是截断误差。即使使用无限精度算术，它也存在，因为它是由截断无限泰勒级数来形成算法造成的。

舍入误差

舍入误差是由于计算设备无法处理某些数字而产生的。此类数字需要舍入到某个近似值，该近似值取决于设备用于表示数字的字长。