数值方法/数值积分

<< 数值方法

通常，我们需要找到一个函数的积分，该函数可能难以解析地积分（即，作为定积分）或不可能（该函数仅作为一组值存在）。

下面列出了几种近似该积分的方法。

梯形法则

考虑一些函数，可能是未知的，$f(x)$，在间隔 [a,b] 上具有已知值，在 n+1 个等间距点 x_i 上，间距为 $h={(b-a) \over n}$，$x_{0}=a$ 和 $x_{n}=b$.

此外，将第 i 个网格点的函数值表示为 $f(x_{i})$.

使用积分作为“求函数曲线下方面积”的概念，我们可以将间隔的第 i 段上的积分表示为从 $x_{i-1}$ 到 $x_{i}$ 如下：

$\int _{x_{i-1}}^{x_{i}}f(x)\,dx$ = (1)

由于我们可能不知道 $f(x)$ 的反导数，我们必须对其进行近似。梯形法则中的这种近似，不出所料，涉及使用宽度为 h、左高度为 $f(x_{i-1})$、右高度为 $f(x_{i})$ 的梯形来近似 (1)。因此，

(1) $\simeq {1 \over 2}h(f(x_{i-1})+f(x_{i}))$ = (2)

(2) 为我们提供了对曲线下方的单个间隔面积的近似值，并且必须重复以覆盖整个间隔。

对于 n = 2 的情况，

$\int _{x_{a}}^{x_{b}}f(x)\,dx\simeq {1 \over 2}h(f(x_{0})+f(x_{1}))+{1 \over 2}h(f(x_{1})+f(x_{2}))$ = (3)

将(3)式右侧的同类项合并，得到

${1 \over 2}h(f(x_{0})+f(x_{1})+f(x_{1})+f(x_{2}))$

或者

${1 \over 2}h(f(x_{0})+2f(x_{1})+f(x_{2}))$

现在，将h代入并整理，得到

${(b-a) \over 2\cdot 2}(f(x_{0})+2f(x_{1})+f(x_{2}))$

为了引出梯形法则的一般形式，现在考虑n = 4的情况，

$\int _{x_{a}}^{x_{b}}f(x)\,dx\simeq {1 \over 2}h(f(x_{0})+f(x_{1}))+{1 \over 2}h(f(x_{1})+f(x_{2}))+{1 \over 2}h(f(x_{2})+f(x_{3}))+{1 \over 2}h(f(x_{3})+f(x_{4}))$

与n=2情况类似，我们得到

${(b-a) \over 2\cdot 4}(f(x_{0})+2(f(x_{1})+f(x_{2})+f(x_{3}))+f(x_{4}))$

推广到一般情况，当n = N时，

$\int _{x_{a}}^{x_{b}}f(x)\,dx\simeq {(b-a) \over 2\cdot n}(f(x_{0})+2(\sum _{k=1}^{N}f(x_{k}))+f(x_{n}))$

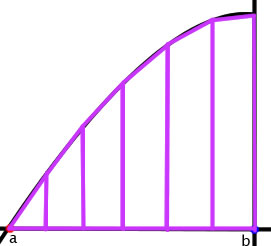这是梯形法则的图形表示，这里$y=-x^{2}+5$.

示例

将 $\int _{0}^{1}x^{3}\,dx$ 近似到 5% 以内。

首先，由于该函数可以精确积分，让我们进行积分，以验证我们的答案。

$\int _{0}^{1}x^{3}\,dx=\left[{x^{4} \over 4}\right]_{0}^{1}={1 \over 4}=0.25$ = (4)

我们将从间隔大小为 1 开始，只考虑端点。

$f(0)=0$

$f(1)=1$

(4) $\simeq {(1-0) \over (2\cdot 1)}(f(0)+f(1))={1 \over 2.1}(0+1)={1 \over 2}=0.5$

相对误差 = $\left|{(0.5-0.25) \over 0.25}\right|=1$

嗯，对于我们的目的来说有点高。所以，我们将间隔大小减半到 0.5 并添加到列表中

$f(0.5)=0.125$

(4) $\simeq {(1-0) \over (2\cdot 2)}(f(0)+2f(0.5)+f(1))={1 \over 2\cdot 2}(0+2(0.125)+1)={1.25 \over 4}=0.3125$

相对误差 = $\left|{(0.3125-0.25) \over 0.25}\right|=0.25$

仍然高于 0.01，但比初始步骤有了很大的改善。我们将以相同的方式继续，计算 $f(0.25)$ 和 $f(0.75)$，四舍五入到小数点后四位。

$f(0.25)=0.0156$

$f(0.75)=0.4219$

(4) $\simeq {(1-0) \over (2\cdot 4)}(0+2(0.0156+0.125+0.4219)+1)={1 \over 8}(2.2150)=0.2656$

相对误差 = $\left|{(0.2656-0.25) \over 0.25}\right|=0.0624$

我们正在朝着正确方向前进。继续，间隔大小为 0.125，并像之前一样进行舍入。

$f(0.125)=0.0020$

$f(0.375)=0.0527$

$f(0.625)=0.2441$

$f(0.875)=0.6699$

(4) $\simeq {(1-0) \over (2\cdot 8)}(0+2(0.0020+0.0156+0.0527+0.0125+0.2441+0.4219+0.6699)+1)={1 \over 16}(4.0624)=0.2539$

相对误差 = $\left|{(0.2539-0.25) \over 0.25}\right|=0.0156$

由于我们的相对误差小于 5%，因此我们停止计算。

误差分析

令 y=f(x) 在 [x₀,x_n] 中连续、行为良好且具有连续导数。我们在 x=x₀ 处展开 y 的泰勒级数，因此 -
$\int _{x_{0}}^{x_{1}}y\,dx=\int _{x_{0}}^{x_{1}}[y_{0}+(x-x_{0})y'_{0}+(x-x_{0})^{2}y''_{0}/2!+......]\,dx$

辛普森法则

考虑某个函数 $y=f(x)$，它可能未知，但在区间 [a,b] 上有 n+1 个等间距点的已知值，则定义为

$\int _{x_{0}}^{x_{n}}f(x)\,dx\simeq {1 \over 3}h{\bigg \{}f(x_{0})+f(x_{n})+2{\Big (}f(x_{2})+f(x_{4})+...+f(x_{n-2}){\Big )}+4{\Big (}f(x_{1})+f(x_{3})+...+f(x_{n-1}){\Big )}{\bigg \}}$

其中 $h={(b-a) \over n}$ 以及 $x_{0}=a$ 以及 $x_{n}=b$.

示例

使用 $n=6$ ($n$ 必须为偶数) 计算 $\int \limits _{0}^{1.2}{x\left({8-x^{3}}\right)^{\frac {1}{2}}dx}$。

解：这里 $f(x)=x\left({8-x^{3}}\right)^{\frac {1}{2}}$

由于 $a=0$ 以及 $b=1.2$，所以 $h={\frac {b-a}{n}}={\frac {1.2-0}{6}}=0.2$

现在，当 $a=x_{0}=0$ 时，$f(x_{0})=0$

由于 $x_{n}=x_{n-1}+h$，因此对于 $x_{1}=0.2$，$x_{2}=0.4$，$x_{3}=0.6$，$x_{4}=0.8$，$x_{5}=1$，$x_{6}=b=1.2$，对应的值为 $f(x_{1})=0.7784$，$f(x_{2})=1.58721$，$f(x_{3})=1.6740$，$f(x_{4})=2.1891$，$f(x_{5})=2.6458$，$f(x_{6})=3.0053$

未完待续... 即将完成

辛普森 3/8 法则

被称为“辛普森 3/8 法则”的数值积分技术归功于英国莱斯特郡的数学家托马斯·辛普森（1710-1761）。他还研究了数值插值和概率论领域。

定理（辛普森 3/8 法则）考虑在区间 上的函数 ，其中 ， ，和 。辛普森 3/8 法则是

   .   

这是一个对区间 上的函数积分的数值近似，我们有以下表达式

   .  

辛普森 3/8 法则的余项为 ，其中 在 ，之间，且有以下等式

   .

证明 辛普森 3/8 法则 辛普森 3/8 法则

复合辛普森 3/8 法则

   Our next method of finding the area under a curve  is by approximating that curve with a series of cubic segments that lie above the intervals  .  When several cubics are used, we call it the composite Simpson's 3/8 rule.  

定理（复合辛普森 3/8 法则）考虑在区间 上的函数 。假设区间被等宽的 子区间细分，使用等间距的采样点 。复合辛普森 3/8 法则对于 子区间是

   .  

这是一个对区间 上的函数积分的数值近似，我们写作

   .  

证明 辛普森 3/8 法则 辛普森 3/8 法则

复合辛普森 3/8 法则的余项

推论（辛普森 3/8 法则：余项）假设 被细分为宽度的 子区间。复合辛普森 3/8 法则

   .  

是一个对积分的数值近似，并且

   .  

此外，如果 ，则存在一个值 ，使得误差项具有以下形式

   .  

这使用“大 O 符号”表示。

备注。当步长缩小到原来的 时，余项应该大约缩小到原来的 。

算法 复合辛普森 3/8 法则。为了近似积分

   ,  

在等间距采样点 上采样，其中 。注意， 和 。

动画 (辛普森 3/8 法则 辛普森 3/8 法则)。指向动画的互联网超链接。

计算机程序 辛普森 3/8 法则 辛普森 3/8 法则

Mathematica 子程序 (辛普森 3/8 法则)。面向对象编程。

示例 1. 使用辛普森 3/8 法则，当 m = 1, 2, 4 时，数值近似积分 。 解答 1.

示例 2. 使用辛普森 3/8 规则，当 m = 10, 20, 40, 80, 160 时，数值逼近积分。解 2.

示例 3. 求解积分的解析值（即求解“真值”）。解 3.

示例 4. 使用示例 3 中的“真值”，求解示例 2 中辛普森 3/8 规则逼近的误差。解 4.

示例 5. 当步长缩减为 的时候，误差项应该大约缩减为 。探索这种现象。解 5.

示例 6. 使用辛普森 3/8 规则，当 m = 1, 2, 4 时，数值逼近积分。解 6.

示例 7. 使用辛普森 3/8 规则，当 m = 10, 20, 40, 80, 160 时，数值逼近积分。解 7.

示例 8. 求解积分的解析值（即求解“真值”）。解 8.

示例 9. 使用示例 8 中的“真值”，求解示例 7 中辛普森 3/8 规则逼近的误差。解 9.

示例 10. 当步长缩减为 的时候，误差项应该大约缩减为 。探索这种现象。解 10.

辛普森 3/8 规则的各种场景和动画。

示例 11. 令 在 上。使用辛普森 3/8 规则来逼近积分的值。解 11.

动画 (辛普森 3/8 法则 辛普森 3/8 法则)。指向动画的互联网超链接。

本科生研究经验

数值积分的辛普森规则 数值积分的辛普森规则 网页链接和文章书目。

参考资料和进一步阅读

• Eric W. Weisstein. "梯形法则." 来自 MathWorld--Wolfram 网页资源. https://mathworld.net.cn/TrapezoidalRule.html
• Davis, P. J., & Rabinowitz, P. (2007). 数值积分方法. Courier Corporation.

---

首页 - 数学书架 - 数值方法