OPT 设计

输出变压器设计基础

电子管输出变压器设计

本书的目的是向世界展示如何设计输出变压器或 OPT，以及需要考虑哪些因素。

理论

最基本的考虑因素是磁芯在任何电压或频率下都不能发生饱和。这意味着磁芯必须能够承受

$B={\frac {U_{rms}}{4,44NAf}}[T]$

由于直流电流几乎总是存在的（尤其是在单端设计中），我们还必须考虑磁场强度 H

$H={\frac {NI}{lm}}[A/m]$

其中 lm 是磁芯周围的平均磁路长度。

此外，可以证明，初级电感需要从以下事实中得出

$w_{l}L>r_{p}//R_{L}$

其中 RL 是反射负载电阻，rp 是电子管的板极电阻。

这产生了以下公式

$L>(r_{p}//n^{2}Z_{L})/w_{l}$

其中 ZL 是扬声器标称阻抗，n 是变压器的匝数比。

此外，可以证明，当每个电子管的负载为

$R_{L}=2r_{p}$

时，输出功率最大。

知道了这一点，就可以计算出最小电感 L。

然而，小信号模型也对方程高频参数提出了限制。如果 OPT 绕得很仔细（分段绕制，而不是双线绕制Template:Fix/category，并且每层之间至少有一层变压器胶带），主要的高频问题将是所谓的漏电感。计算它的公式是

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

或

$L_{leak}<(r_{p}+R_{L})/w_{h}$$L_{leak}<(r_{p}+R_{L})/w_{h}$

然而，这个参数很难控制。但经验表明，一个重要的因素是，次级绕组必须覆盖整个初级绕组（或两个初级绕组）。另一个想法是，绕组端点不能折叠。最后一点主要可以消除高频谐振。

环形变压器的电感可以表示为

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$

其中

$\mu _{eff}=\mu _{0}{\frac {\mu _{r}}{1+{\frac {lg}{lm}}\mu _{r}}}$$\mu _{eff}=\mu _{0}{\frac {\mu _{r}}{1+{\frac {lg}{lm}}\mu _{r}}}$

其中 lg 是气隙长度，lm 是平均磁路长度。

$\mu _{eff}=\mu _{0}\mu _{r}$

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$

$\mu _{r}$

是铁的相对磁导率，而

$\mu _{0}$

是真空的磁导率。

实际例子

可以证明，单极低通滤波器的滚降在比fh低三倍的频率上仅产生-0,5dB的影响。这意味着如果我们想要在最高可听频率（20kHz）处获得-0,5dB，我们需要一个60kHz的fh。

因为

$w_{h}=2\pi f_{h}$

这意味着泄漏电感小于

$L_{leak}<33mH$

如果我们想在推挽式（PP）中使用KT66管，其中rp=2rp(KT66)=2500欧姆。请注意，PP设计中的RL是每个管子负载的4倍。因此，在我们的案例中，最佳板间负载为10k欧姆。

同样的情况也适用于单极高通滤波器，因此-0.5dB@10Hz的fl为3,3Hz。因此电感需要大于

$L>95H$

如果我们想使用建议的铁芯尺寸，我们得到

$A=6,25\cdot 10^{-4}[m^{2}]$

和

$l_{m}=0,196[m]$

因为P1+P2需要承受230V@15Hz，而变压器铁芯的常见最大磁通密度约为

$B=1,6T$

现在可以使用第一个方程计算匝数。这给出

$N=3453$

将此代入初级电感方程，我们得到

$L=0,041\mu _{r}[H]$

因为我们想在A类推挽式配置中使用OPT，所以我们不必过多考虑由于管子老化和扬声器阻抗随频率变化而产生的直流电流。但是，建议OPT应该能够承受至少通过两个初级的10mADC直流电流。在SE配置中，需要所谓的空气隙，但这在环形变压器中无法（轻易）实现，这使我们依赖于所用铁芯的BH环路的宽度。

对于我们变压器中10mA的直流电流，磁场强度为

$H=176[A/m]$

我们希望至少剩下L/3=30H。

方程推导

本段将解释上述使用方程的推导。

标准OPT使用

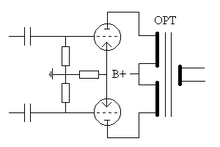标准OPT使用

这张图片展示了OPT在推挽式（PP）配置中的使用方式。但是，下面的理论也适用于单端式（SE）配置。

OPT小信号模型

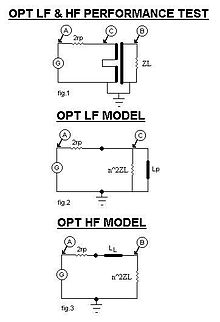OPT小信号模型

这张图片展示了OPT的小信号模型。

图1显示了简单的OPT连接，即通过两个板极电阻rp（由于PP）由信号发生器G驱动。

图2显示了在低频下发生的情况，此时OPT作为普通变压器工作。因此，反射阻抗为

$R_{L}=n^{2}Z_{L}$

其中 n 是 OPT 的匝数比，ZL 是扬声器的阻抗。

图 3 显示了在高频情况下发生的情况，其中漏 inductance LL 由于前面提到的特殊绕线技术而占主导地位，胜过层间电容。上面的表达式仍然成立。

变压器基础

考虑一个理想的变压器，没有铁损或铜损。那么输出功率将等于输入功率。

如果您将高压转换成低压，那么您将在二次侧获得比一次侧输入的电流更大的电流。

所以如果

$Pin=U1\cdot I1$

那么

$Pout=U2\cdot I2$

并且如果

$U2=U1/n$

那么可以推导出

$I2=n\cdot I1$

最后

$U2/I2=1/n^{2}\cdot U1/I1$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$U1/I1=n^{2}\cdot U2/I2$

小信号模型评估

在图 2 中使用诺顿和戴维宁电路理论时，我们得到

$wL_{p}>(2rp//n^{2}Z_{L})$

然而，在图 3 中，我们可能只是意识到这样一个事实，即

$wL_{L}<(2rp+n^{2}Z_{L})$

因为这是 LL 的 reactance 变得占主导地位的地方。

标准滤波器特性

想象一个单极高通滤波器。那么你可能有一个与接地电阻串联的电容器。然后拉普拉斯传递函数得出

$Uo/Uin=R/(R+1/sC)$

或者简化为

$Uo/Uin=1/(1+1/(sRC))$

将

$w_{0}=1/RC$

我们得到

$Uo/Uin=1/(1+w_{0}/s)$

将 s=jw，我们得到

$Uo/Uin=1/(1+w_{0}/jw)$

并且传递函数的幅度变为

$Uo/Uin=1/{\sqrt {1+(w_{0}/w)^{2}}}$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$Uo/Uin=1/{\sqrt {1+(f_{0}/f)^{2}}}$

其中 f 是频率。

将

$f=3f_{0}$

我们得到

$Uo/Uin=-0,46dB$

场磁学

在本段中，我们将向世界展示电磁学的基本原理。

麦克斯韦方程组

麦克斯韦方程组的标准形式为

$\nabla \cdot \mathbf {D} =\rho _{f}$

$\nabla \cdot \mathbf {B} =0$

$\nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}$

$\nabla \times \mathbf {H} =\mathbf {J} _{f}+{\frac {\partial \mathbf {D} }{\partial t}}$

第一个方程式，即高斯定律，描述了电荷是如何产生电场的。

第二个方程式指出，不存在“磁荷”，即所谓的磁单极子。

第三个方程式，即法拉第定律，描述了磁场变化是如何产生电场的。

第四个方程式，即安培定律（含麦克斯韦修正项），描述了电场变化是如何产生磁场的。

已用量列表

E : 电场强度 [V/m]

D : 电通量密度 [As/m^2]

H : 磁场强度 [A/m]

B : 磁通量密度 [Vs/m^2]

J_f : 自由电流密度 [A/m^2]

积分形式

$\oint _{S}\mathbf {D} \cdot d\mathbf {s} =\int _{V}\rho _{f}dv$

$\oint _{S}\mathbf {B} \cdot d\mathbf {s} =0$

$\oint _{C}\mathbf {E} \cdot dl=-\int _{S}{\partial \mathbf {B} \over \partial t}\cdot d\mathbf {s}$

$\oint _{C}\mathbf {H} \cdot dl=\int _{S}\mathbf {J} _{f}\cdot d\mathbf {s} +\int _{S}{\partial \mathbf {D} \over \partial t}\cdot d\mathbf {s}$

边界条件

从介质 1 到介质 2 麦克斯韦方程组给出

$\mathbf {\hat {n}} \cdot (\mathbf {D} _{2}-\mathbf {D} _{1})=\sigma _{f}$

$\mathbf {\hat {n}} \times (\mathbf {E} _{2}-\mathbf {E} _{1})=0{\mbox{ or }}\mathbf {E} _{2t}=\mathbf {E} _{1t}$

$\mathbf {\hat {n}} \cdot (\mathbf {B} _{2}-\mathbf {B} _{1})=0$

$\mathbf {\hat {n}} \times (\mathbf {H} _{2}-\mathbf {H} _{1})=\mathbf {K} _{f}{\mbox{ or }}\mathbf {H} _{2t}-\mathbf {H} _{1t}=\mathbf {K} _{f}\times \mathbf {\hat {n}}$

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$

$\sigma _{f}$ 是表面电荷密度，K_f 是介质间的自由表面电流强度。

法拉第定律

考虑法拉第定律，我们从麦克斯韦方程组中得到

$\oint _{C}Edl=-{\frac {d}{dt}}\int _{S}BdS$

如果我们定义

$V=\oint _{C}Edl$=在曲率 C 上感应的电动势 [伏特]

和

$\Phi =\int _{S}BdS$=穿过表面 S 的磁通量 [伏秒或韦伯]

那么我们得到

$V=-{\frac {d\Phi }{dt}}$ [伏特]

如果我们使用几匝 N 的线圈，我们将得到

$V=-N{\frac {d\Phi }{dt}}$ [伏特]

如果磁通量流经铁芯，其中

$\mu _{r}>>1$

磁通量将只停留在铁芯中，产生与匝数比 n 成正比的二次电压。

铁芯中的磁通密度

根据法拉第定律，我们有

$\Phi =\int _{S}BdS$

由于表面 S 没有变化，我们有

$\Phi =BS$

使用方程式

$V=-N{\frac {d\Phi }{dt}}$

然后我们得到

$V=-NS{\frac {dB}{dt}}$

正弦磁通密度产生

$B=B_{max}\cdot sin(wt)$

因此

$V=-NSB_{max}\cdot w\cdot cos(wt)$

当发生最大值时

$V=NSB_{max}w$

因此

$B_{max}={\frac {V}{NSw}}$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$B_{max}={\frac {V}{2\pi NAf}}$

其中 A 已替代 S

如果电压是正弦波

$V={\sqrt {2}}V_{rms}$

我们得到

$B_{max}={\frac {V_{rms}}{4,44NAf}}$

铁芯中的磁场强度

根据麦克斯韦方程组，我们得到

$\oint _{C}\mathbf {H} \cdot dl=NJ_{f}S=NI$

因为我们只考虑直流和均匀表面。

所以如果我们使用环形磁芯，那么

$H2\pi r=NI$

并且如果

$l_{m}=2\pi r$

那么

$H={\frac {NI}{l_{m}}}$

气隙导致的有效磁导率

再次应用安培环路定律，我们得到

$\oint _{C}\mathbf {H} \cdot dl=NI$

这里我们也有

$B_{f}=B_{g}$

但在磁芯中，我们会有

$H_{f}=B_{f}/\mu$

而在气隙中

$H_{g}=B_{f}/\mu _{0}$

这给出

${\frac {B_{f}}{\mu }}(2\pi r-lg)+{\frac {B_{f}}{\mu _{0}}}l_{g}=NI$

这可以改写为

${\frac {B_{f}}{\mu _{0}}}({\frac {lm}{\mu _{r}}}+l_{g})=NI$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

${\frac {B_{f}}{\mu _{eff}}}l_{m}=NI$

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$$L={\frac {\mu _{eff}N^{2}h}{2\pi }}\ln {\frac {b}{a}}[H]$

$l_{m}=2\pi r-lg$

这给出

$\mu _{eff}=\mu _{0}{\frac {l_{m}}{{\frac {l_{m}}{\mu _{r}}}+l_{g}}}$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$\mu _{eff}=\mu _{0}{\frac {\mu _{r}}{1+{\frac {l_{g}}{l_{m}}}\mu _{r}}}$

环形磁芯电感

考虑柱坐标系。然后我们得到

$B=a_{\phi }B_{\phi }$

$dl=a_{\phi }rd{\phi }$

$\oint _{C}B\cdot dl=\int _{0}^{2\pi }B_{\phi }rd\phi =2\pi rB_{\phi }$

由于路径包围了总电流 NI，因此我们有

$2\pi rB_{\phi }=\mu _{eff}NI$

知道关系

$B=\mu H$

很容易与之前的等式联系起来，因此

$B_{\phi }={\frac {\mu _{eff}NI}{2\pi r}}$

和

$\Phi =\int _{S}Bds=\int _{S}a_{\phi }{\frac {\mu _{eff}NI}{2\pi r}}\cdot a_{\phi }hdr$

等于

$\Phi ={\frac {\mu _{eff}NIh}{2\pi }}\int _{a}^{b}{\frac {dr}{r}}={\frac {\mu _{eff}NIh}{2\pi }}\ln {\frac {b}{a}}$

使用磁通链为

$N\Phi$

并且小信号电感独立于电流，我们得到

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}ln{\frac {b}{a}}$

C 型铁芯电感

这个不容易计算，但如果我们可以通过以下方式定义平均磁路长度，我们可以做一些近似

$lm=2\cdot c+2\cdot d$

其中 c 是最短边（在铁芯中心）和 d 是最长边。

将此近似为圆形环形形状，我们得到

$r_{mean}={\frac {lm}{2\pi }}$

在此基础上加上铁芯厚度的一半得到 b，减去铁芯厚度的一半得到 a。然后我们可以重复使用

$L={\frac {\mu _{eff}N^{2}h}{2\pi }}ln{\frac {b}{a}}$

这应该相当有效，因为磁通由于以下原因而保留在铁芯中

$\mu _{r_{e}ff}>>1$

优化管放大器负载

三极管的最大可用功率

如果我们考虑

$i(t)=i_{a}*sin(wt)$

$u(t)=u_{a}*sin(wt)$

并认识到

$i_{a}=I_{a}$

$u_{a}=U_{a}-2R_{i}I_{a}$

输出功率可以写成

$P=u_{a}*i_{a}/2=U_{a}I_{a}/2-R_{i}I_{a}^{2}$

并对 Ia 求导得到

${\frac {dP}{dI_{a}}}=U_{a}/2-2R_{i}I_{a}=0$

最大值为

$I_{a}={\frac {U_{a}}{4R_{i}}}$

因此

$P_{max}={\frac {U_{a}^{2}}{8R_{i}}}-{\frac {U_{a}^{2}}{16R_{i}}}={\frac {U_{a}^{2}}{16Ri}}$

从图中可以看出

$U_{a}=2R_{i}I_{a}+R_{a}I_{a}=I_{a}(2R_{i}+R_{a})={\frac {U_{a}}{4R_{i}}}*(2R_{i}+R_{a})$

其中 Ua 被消去，因此

$1=1/2+{\frac {R_{a}}{4R_{i}}}$

$w_{h}L_{leak}<(r_{p}+R_{L})$$w_{h}L_{leak}<(r_{p}+R_{L})$

$2=1+{\frac {R_{a}}{2R_{i}}}$

因此

$2R_{i}=R_{a}$

证明这一点的更简单方法是通过观察图像

$u_{a}=U_{a}-2R_{i}I_{a}=U_{a}-R_{a}I_{a}$

这最终证明了三极管的最佳负载是其内部阻抗的两倍。但是，应该指出的是，板电压应该是限制因素，对于板耗散成为问题的高电压，Ra 必须更高。

值得注意的是，在这种情况下，效率只有 25%，我们可以通过代入证明这一点

$P_{a}=U_{a}*I_{a}=U_{a}^{2}/4R_{i}$

其中

$P_{out}=i_{a}*u_{a}/2=I_{a}*(U_{a}-2R_{i}I_{a})/2={\frac {U_{a}}{4R_{i}}}(U_{a}-2R_{i}{\frac {U_{a}}{4R_{i}}})/2={\frac {U_{a}^{2}}{4R_{i}}}(1-1/2)/2$

因此

${\frac {P_{out}}{P_{a}}}=1/4$