二维逆问题/Dirichlet-to-Neumann 映射的核

The continuous analog of the matrix representation of a Dirichlet-to-Neumann operator for a domain  $\Omega$  is its kernel. It is a distribution defined on the Cartesian product of the boundary of the domain w/itself, such that if

$\Lambda f=g,$ 则 $g(\phi )=\int _{\partial \Omega }K(\phi ,\theta )f(\theta )d\theta ,$ 其中 $\phi$ 和 $\theta$ 使用弧长测度参数化边界。

For the case of the half-plane w/constant unit conductivity the kernel can be calculated explicitly. It's a convolution, because the domain in consideration is shift invariant:

$K(\phi ,\theta )=k(\phi -\theta ),$ 其中 k 是线上的一种分布。因此，计算简化为对一个 $\delta _{0}$ -函数在原点的Dirichlet 问题求解，并在边界线上取外导数。

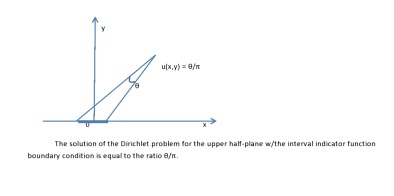
Dirichlet problem for a half-plane — 半平面的 Dirichlet 问题

练习 (**). 完成半平面核 K 的计算，以显示 $K(x,y)={\frac {-1}{\pi (x-y)^{2}}}$ 不在对角线上。

练习 (*). 证明对于旋转不变的区域（圆盘，导电率仅取决于半径），Dirichlet-to-Neumann 映射的核是卷积。

希尔伯特变换给出了调和函数的边界值与其调和共轭之间的对应关系。 $H:u|_{\partial \Omega }\rightarrow v|_{\partial \Omega },$ 其中 $f(z)=u(z)+iv(z)$ 是域中的解析函数。

对于复上半平面的情况，希尔伯特变换由以下公式给出： $Hf(y)={\frac {1}{\pi }}\ {\text{p.v.}}\int _{-\infty }^{\infty }{\frac {f(x)}{y-x}}dx.$

练习 (*). 对上述公式进行积分符号求导，得到半平面 Dirichlet-to-Neumann 算子的核表示。

To define discrete Hilbert transform for a planar network, the network together w/its dual is needed.