OpenGL 编程/现代 OpenGL 教程 轨迹球
轨迹球是一种使用鼠标自然旋转物体的工具。
想象一个位于屏幕后面的虚拟球。通过用鼠标点击它,你就可以捏住它,通过移动鼠标,你可以让球绕其中心旋转。相同的旋转将应用于 OpenGL 场景中的物体!虽然直观地实现,但事实证明它在使用上并不直观。
相反,沿着你点击球体的点和当前点之间的方向旋转,旋转角度为弧长两倍,这种方式更容易使用和实现。
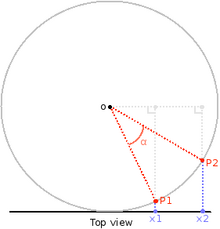
右侧的图示显示了虚拟球的俯视图。底部的黑线是屏幕,x1 和 x2 是拖动过程中两次连续的鼠标位置。这是在 2D 中显示的,但相同的原理适用于 3D。
目标是计算 α 角和旋转轴。当你开始认真使用 OpenGL 时,你会发现数学是必不可少的。我们将用到勾股定理、向量点积和叉积。
我们将
- 将屏幕坐标(以像素为单位)转换为相机坐标(以 [-1, 1] 为单位)
- 计算向量 OP1 和 OP2,它们是与鼠标点击匹配的球体表面上的点
- x 和 y 坐标直接从相机坐标中的点击位置获取
- z 坐标使用经典的勾股定理计算
- 如果 P1 或 P2 距离球体太远(),我们将对其进行归一化以获得球体表面上的最近点
- 我们有,球体的大小为 1(),因此我们使用获取角度。
- 为了获得 3D 中的旋转轴,我们计算,它将提供一个单位垂直向量
GLUT 提供了一种获取鼠标点击和拖动事件的方法
glutMouseFunc(onMouse) 将为每个鼠标点击调用 onMouse(int button, int state, int x, int y),其中
- button 是 GLUT_LEFT_BUTTON、GLUT_MIDDLE_BUTTON 或 GLUT_RIGHT_BUTTON
- state 是 GLUT_DOWN 或 GLUT_UP
- x 和 y 是屏幕坐标,从左上角开始(y 方向与 OpenGL 坐标相反!)
glutMotionFunc(onMotion) 将为任何按钮按下时的每次鼠标移动调用 onMotion(int x, int y),其中 x 和 y 是屏幕坐标。
你还可以使用 glutPassiveMotionFunc(...),它在没有任何按钮按下时,也能以类似的方式处理鼠标移动。
因此,我们添加了两个函数来跟踪左键按下时的鼠标移动
/* Global */
int last_mx = 0, last_my = 0, cur_mx = 0, cur_my = 0;
int arcball_on = false;
/* main() */
glutMouseFunc(onMouse);
glutMotionFunc(onMotion);
void onMouse(int button, int state, int x, int y) {
if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN) {
arcball_on = true;
last_mx = cur_mx = x;
last_my = cur_my = y;
} else {
arcball_on = false;
}
}
void onMotion(int x, int y) {
if (arcball_on) { // if left button is pressed
cur_mx = x;
cur_my = y;
}
}
我们添加了一个新的函数来计算轨迹球表面点
/**
* Get a normalized vector from the center of the virtual ball O to a
* point P on the virtual ball surface, such that P is aligned on
* screen's (X,Y) coordinates. If (X,Y) is too far away from the
* sphere, return the nearest point on the virtual ball surface.
*/
glm::vec3 get_arcball_vector(int x, int y) {
glm::vec3 P = glm::vec3(1.0*x/screen_width*2 - 1.0,
1.0*y/screen_height*2 - 1.0,
0);
P.y = -P.y;
float OP_squared = P.x * P.x + P.y * P.y;
if (OP_squared <= 1*1)
P.z = sqrt(1*1 - OP_squared); // Pythagoras
else
P = glm::normalize(P); // nearest point
return P;
}
我们首先将 x,y 屏幕坐标转换为 [-1,1] 坐标(并反转 y 坐标)。然后我们使用勾股定理来检查 OP 向量的长度并计算 z 坐标,如上所述。
/* onIdle() */
if (cur_mx != last_mx || cur_my != last_my) {
glm::vec3 va = get_arcball_vector(last_mx, last_my);
glm::vec3 vb = get_arcball_vector( cur_mx, cur_my);
float angle = acos(min(1.0f, glm::dot(va, vb)));
glm::vec3 axis_in_camera_coord = glm::cross(va, vb);
glm::mat3 camera2object = glm::inverse(glm::mat3(transforms[MODE_CAMERA]) * glm::mat3(mesh.object2world));
glm::vec3 axis_in_object_coord = camera2object * axis_in_camera_coord;
mesh.object2world = glm::rotate(mesh.object2world, glm::degrees(angle), axis_in_object_coord);
last_mx = cur_mx;
last_my = cur_my;
}
一旦我们获得了 OP1 和 OP2(这里称为 va 和 vb),我们就可以使用 acos(dot(va,vb)) 计算角度。
由于我们使用的是float变量,可能会出现精度问题:dot可能返回的值略大于1,acos将返回nan,这意味着无效的浮点数。结果是我们的旋转矩阵将被全部搞乱,通常我们的物体将从屏幕上消失!为了解决这个问题,我们用1.0的最大值限制该值。
另一个技巧是将旋转轴从相机坐标转换为物体坐标。当相机和物体放置不同时,这很有用。例如,如果你在 Y 轴上将物体旋转 90 度(“将头部转向”右侧),然后用鼠标进行垂直移动,你会在相机 X 轴上进行旋转,但对于物体来说,它应该变成 Z 轴上的旋转(平面桶式滚动)。通过将轴转换为物体坐标,旋转将尊重用户在相机坐标系中工作(所见即所得)。为了从相机坐标系转换为物体坐标系,我们取 MV 矩阵(来自 MVP 矩阵三元组)的逆矩阵。
最后,我们可以像往常一样使用glm::rotate应用我们的变换:)
- 旋转角度是否与鼠标移动成正比?尝试在虚拟球体的边界附近移动。
- 当鼠标离得太远时,虚拟球将停止滚动。其他鼠标控制是可能的。例如,研究在 Blender 3D 建模器中使用中键拖动的工作原理。
- 尝试不同的滚动速度,方法是将旋转角度相乘。







