OpenSCAD 用户手册/示例/Strandbeest

摘要

本章介绍如何使用 OpenSCAD 动画化像 strandbeest 这样的复杂机制。

该模型并非用于 3D 打印。

源代码只是一个文件，没有使用外部库，已在 OpenSCAD 版本 2015.03 中测试。

目标受众 / 先决条件

您需要安装 OpenSCAD 并需要了解如何使用 OpenSCAD 的基本知识。

了解几何学的基本知识对于理解如何在纸上构建连杆以及如何使用用于计算连杆的函数至关重要。理解三角学有助于理解函数背后的数学原理，但不是严格必需的。

准备

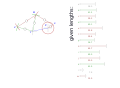
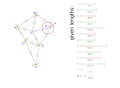
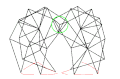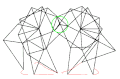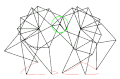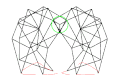
首先，我们需要一个带有常量的图纸。

Theo Jansen 在他的网站上发布了这些数字：[1]（视频“The Legsystem”，3:36）或在网页的存档版本上：[2]

我建议给点命名。命名可以是任意的。我使用了 Z..S 来避免与长度 a..m 混淆。

打印出图纸以方便在上面涂写可能非常有用。

手工建造

现在我们必须考虑如何手工构建机制。

我们需要一个不可折叠的圆规、一把尺子、纸和一支铅笔。

不可折叠的圆规和尺子

我们将原点 Z 设置为任意点。对于 Y，我们向下 l，向左 a。曲柄 m 可以处于任意角度。绘制曲柄会得到点 X。

从此点开始，我们构造由两个点和两个长度定义的三角形。

在几何学中，这是 SSS 案例（用给定的三条边构造三角形，另请参见解三角形#给定三条边（SSS））。

在纸上，这可以使用圆规轻松解决。

让我们首先将圆规设置为长度 b，然后将圆规放在点 Y。然后我们将圆规设置为长度 j，并将圆规放在点 X。圆弧的交点即为点 W。

请注意，当给出两个点和两个长度时，总是存在两个解，即交点。鉴于我们已经知道机制的一般形状，我们知道我们需要哪一个。但请记住这一点，因为它将在稍后使用。

其余部分或多或少都是“重复”。

几何构造说明

约定

长度用小写字母表示
点用大写字母表示
用于构造的线和圆弧后面有一个'

说明[编辑 | 编辑源代码]
构造点 Z
绘制一条水平线 h
绘制一条垂直线 v，与水平线 h 相交
标记 h 和 v 交点为点 Z

这将是此构造的原点以及腿机构的曲柄轴
构造点 Y
从 h 向下 l 距离绘制一条水平线 h'
从 v 向左 a 距离绘制一条垂直线 v'
标记 h' 和 v' 的交点为固定点 Y
构造点 X
通过 Z 绘制一条线 m'，添加一个任意角度（该角度即为曲柄角度）
从点 Z 以半径 m 绘制一条圆弧，圆弧 n 和点 Z 的交点即为曲柄枢轴 X

从 Z 绘制一条线 m 到 X
构造点 W（SSS 案例）
从点 X 以半径 j 绘制一条圆弧 j'
从点 Y 以半径 b 绘制一条圆弧 b'
圆弧 j' 和 b' 的交点即为点 W

从 X 绘制一条线 j 到 W
从 Y 绘制一条线 b 到 W
构造点 V（SSS 案例）
从点 W 以半径 e 绘制一条圆弧 e'
从点 Y 以半径 d 绘制一条圆弧 d'

从 W 绘制一条线 e 到 V
从 Y 绘制一条线 d 到 V
圆弧 e' 和 d' 的交点即为点 V
构造点 U（SSS 案例）
从点 Y 以半径 c 绘制一条圆弧 c'
从点 X 以半径 k 绘制一条圆弧 k'

从 Y 绘制一条线 c 到 U
从 X 绘制一条线 k 到 U
圆弧 c' 和 k' 的交点即为点 U
构造点 T（SSS 案例）
从点 V 以半径 f 绘制一条圆弧 f'
从点 U 以半径 g 绘制一条圆弧 g'
圆弧 f' 和 g' 的交点即为点 T

从 V 绘制一条线 f 到 T
从 U 绘制一条线 g 到 T
构造点 S（SSS 案例）
从点 T 以半径 h 绘制一条圆弧 h'
从点 U 以半径 i 绘制一条圆弧 i'
圆弧 f' 和 g' 的交点即为点 S这是机制的“脚”

从 T 绘制一条线 h 到 S
从 U 绘制一条线 i 到 S

步骤 1
步骤 2
步骤 3
步骤 4
步骤 5
步骤 6
步骤 7
步骤 8

给定长度

    a=38.0
    b=41.5
    c=39.3
    d=40.1
    e=55.8
    f=39.4
    g=36.7
    h=65.7
    i=49.0
    j=50.0
    k=61.9
    l= 7.8
    m=15.0

点

 Z fix point, origin, crank axis
 Y fix point
 X crank axis
 W
 V
 U
 T
 S foot

计算机几何

要将此转换为源代码，我们需要一些几何函数。

其中大部分是简单的三角函数。

值得注意的是“atan2”和余弦定理，在函数 VVLL2D（**V**ector **V**ector **L**ength **L**ength 2D）中实现。

关于 atan2 的所有内容都可以从维基百科中了解到：atan2

对于余弦定理，我推荐这篇文章：http://www.dummies.com/education/math/trigonometry/use-the-law-of-cosines-with-sss/

请记住，对于两个点和两个长度，要么有两个解，要么没有解。目前我们可以忽略没有解的情况，因为我们知道该机构不会卡住。为了得到方程的另一个解，只需交换参数即可。

绘图函数

我们还需要一些“绘图”模块。为了简单起见，该模块命名为 rod，它只需从一个点画到另一个点即可。

实现

现在我们有了计算点的几何函数、一个在两点之间绘制杆的模块，以及对如何构建对象的总体理解，实现本身出奇地容易。

腿部模块

让我们看一下腿部模块。

计算代码只有八行，绘制杆的代码只有十二行。

沙滩兽

对于完整的沙滩兽，我们只需要六条腿，它们之间要有一定的间距和角度偏移。

源代码

//------------------------
// Trigonometry Functions
//------------------------
function add2D(v1=[0,0],v2=[0,0]) =
    [
        v1[0]+v2[0],
        v1[1]+v2[1]
    ];
  
function sub2D(v1=[0,0],v2=[0,0]) = 
    [
        v1[0]-v2[0], 
        v1[1]-v2[1]
    ];

function addAngle2D(v1=[0,0],ang=0,l=0) = 
    [
        v1[0]+cos(ang)*l,
        v1[1]-sin(ang)*l
    ];

function getAngle2D(v1,v2=[0,0]) =
  atan2(
    (v2[0]-v1[0]), //dx
    (v2[1]-v1[1])  //dy
  );

function scale2D(v1=[0,0],c=1)= 
  [
    v1[0]*c,
    v1[1]*c,
  ];

function length2D(v1,v2=[0,0])=
  sqrt(
      (v1[0]-v2[0])*(v1[0]-v2[0])
      +
      (v1[1]-v2[1])*(v1[1]-v2[1])
    );

//Law of cosines
function VVLL2D(v1,v2,l1,l2) =
  let(sAB = length2D(v1,v2))
  let(ang12=getAngle2D(v2,v1))
  let(ang0=
        acos(
          (l2*l2-l1*l1-sAB*sAB)/
          (-abs(2*sAB*l1))
        ))
        
  addAngle2D(
    v1=v1,
    ang=ang0+ang12-90,
    l=-l1
  );

//----------------------
// modules (Graphic Functions)
//----------------------
// draw "rod" from v1 to v2 with thickness t
module rod(v1=[0,0],v2=[0,0],t=6){
		ang1=getAngle2D(v1,v2);
    len1=length2D(v1,v2);
		translate([v1[0],v1[1]])
		rotate([0,0,-ang1]){
			translate([0,0,0]){
					cylinder(r=t,h=t+2,center = true);
			}
			translate([-t/2,0,-t/2]){
				cube([t,len1,t]);
			}
		}
}

//----------------------
// Leg Module // Jansen mechanism
//----------------------
module leg (
    ang=0,
    a=38.0, //a..m Theo Jansens Constants
    b=41.5,
    c=39.3,
    d=40.1,
    e=55.8,
    f=39.4,
    g=36.7,
    h=65.7,
    i=49.0,
    j=50.0,
    k=61.9,
    l= 7.8,
    m=15.0
    )
{
  Z = [0,0]; //Origin
  X = addAngle2D(Z,ang,m); //Crank / "backbone"
  Y = add2D(Z,[a,l]);
  W = VVLL2D(X,Y,j,b);
  V = VVLL2D(W,Y,e,d);
  U = VVLL2D(Y,X,c,k);
  T = VVLL2D(V,U,f,g);
  S = VVLL2D(T,U,h,i); //Foot
   
  rod(Z, X);
  rod(X, W);

  rod(W, Y);
  rod(W, V);
  rod(Y, V);
  rod(X, U);
  rod(Y, U);
  rod(U, T);
  rod(V, T);
  rod(U, S);
  rod(T, S);
  rod(Z, Y);

  //draw the foot point
  translate(S){
    cylinder(r=8,h=8,center = true); 
  }
}

//----------------------
// Strandbeest
//----------------------
module Strandbeest(ang=$t*360,o=360/3,sgap=20,mgap=50)
{
    {
        color([1, 0, 0]) translate([0,0,sgap*0]) leg(ang+o*0);
        color([0, 1, 0]) translate([0,0,sgap*1]) leg(ang+o*1);
        color([0, 0, 1]) translate([0,0,sgap*2]) leg(ang+o*2);
    }
    mirror(v= [1, 0, 0] ){
        color([1, 0, 0]) translate([0,0,sgap*0]) leg(180-ang-o*0);
        color([0, 1, 0]) translate([0,0,sgap*1]) leg(180-ang-o*1);
        color([0, 0, 1]) translate([0,0,sgap*2]) leg(180-ang-o*2);
    }
    translate([0,0,sgap*2 + mgap])
    {
        color([1, 0, 0]) translate([0,0,sgap*0]) leg(180+ang+o*0);
        color([0, 1, 0]) translate([0,0,sgap*1]) leg(180+ang+o*1);
        color([0, 0, 1]) translate([0,0,sgap*2]) leg(180+ang+o*2);
    }
    translate([0,0,sgap*2 + mgap])   
    mirror(v= [1, 0, 0] ){
        color([1, 0, 0]) translate([0,0,sgap*0]) leg(0-ang-o*0);
        color([0, 1, 0]) translate([0,0,sgap*1]) leg(0-ang-o*1);
        color([0, 0, 1]) translate([0,0,sgap*2]) leg(0-ang-o*2);
    }
}

//leg(ang=$t*360);

rotate([90,180,0]) Strandbeest();

导出动画

OpenSCAD 可以将动画帧导出为 PNG 文件。在 Linux 下，可以使用命令行将这些 PNG 文件转换为 gif。

convert -delay 10 -loop 0 *.png myimage.gif

Convert 是 ImageMagick 的一部分。

然后可以使用 GIMP 对生成的 GIF 进行裁剪（如果需要）。

接下来，在使用此示例时

我建议将源代码分成不同的文件。一种分割方法是

三角函数
绘图函数
詹森机构/腿部
沙滩兽

我建议使用“use”。这允许您在每个文件中包含自检。

为了美化动画，您可以绘制连接腿部的轴线，或者添加支撑框架。

如果您有 3D 打印机，您可以修改代码，以便连接点可以实际旋转。

接下来，在使用不同的方法构建机构时

角度错误/缺少测量值/倾斜

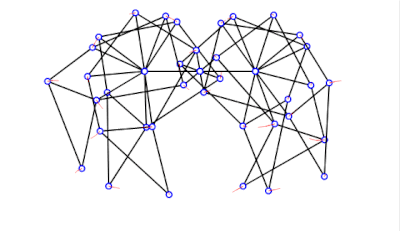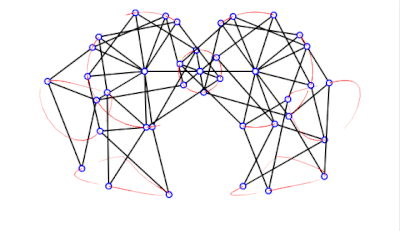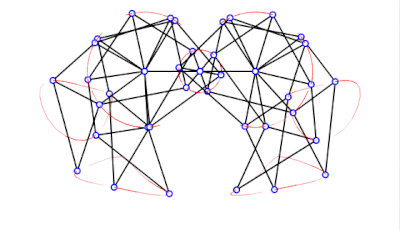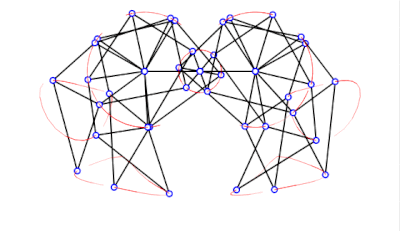
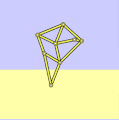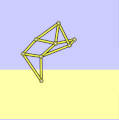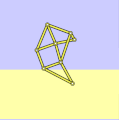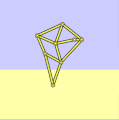
具有正确尺寸的沙滩兽
a = 38.0 l = 7.8
轨迹正确且接地
具有错误尺寸的沙滩兽
a = 38.0 l = 0
轨迹提取并倾斜
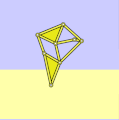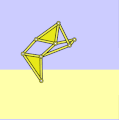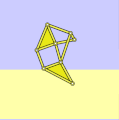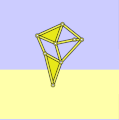
具有错误尺寸的沙滩兽
a = 38.79 l = 0
轨迹正确，但倾斜

示例

Klann R&D，Joe Klann，詹森机构 - Klann 机构比较
- https://web.archive.org/web/20160304035711/http://www.mechanicalspider.com/comparison.html
Adam Savage 的一日建造：踏板驱动的沙滩兽！
- https://www.youtube.com/watch?v=G96YQQ7vW8w?t=740
- https://www.youtube.com/watch?v=G96YQQ7vW8w?t=1018

请注意，这些示例并非为了嘲笑创作者的错误，而是赞扬他们分享了他们的经验，以便我们都能从他们那里学习。

这种错误的发生率更高，因为人们说的是十一个^[1]^[2]个神奇数字，而不是 13 个神奇数字。

（有十一根杆，但两个固定点彼此相距a和l）

三角形

传统上，腿部只是使用杆形成的。

在使用纸张或木材等平板材料进行制造时，认识到一条腿也可以由 2 个三角形和 5 根杆构成，可以简化组装并使机构更加坚固。

以下是一些实际示例

用纸板制成的腿部机构
迷你沙滩兽

准备 3D 打印的模型

一个在 OpenSCAD 中实现的全参数化沙滩兽，包括组装说明，可用于 3D 打印。^[3]

使用相同长度的杆

f=39,4 和 c=39,3 的长度非常接近，因此使用相同长度的杆可以简化组装，而不会对步态造成太大影响。

请注意，在实践中，整个机构都会发生运动和弯曲，地下并非完全平坦，长度和孔洞会存在制造造成的误差。

参考文献

↑ https://ethanzuckerman.com/2007/03/08/theo-jansens-strandbeests/
↑ Linda Leinen (26 September 205). "Theo Jansen: Walking on the Mild Side".
↑ A. Matulich (23 May 2020). "Building the Strandbeest".

[1] ttps://ethanzuckerman.com/2007/03/08/theo-jansens-strandbeests/

[2] Linda Leinen (26 September 205). "Theo Jansen: Walking on the Mild Side".

[3] A. Matulich (23 May 2020). "Building the Strandbeest".

[1]

[2]

[3]