物理习题/静电学

电场叠加原理

1. 用文字和公式说明电场的叠加原理。

图示叠加原理。

在物理学中，电场叠加原理假设，对于所有线性系统，由两个或多个电荷在给定位置和时间引起的净响应是每个电荷单独引起响应的总和。

数学上可以写成

${\vec {E}}={\vec {E}}_{1}+{\vec {E}}_{2}+{\vec {E}}_{3}+...+{\vec {E}}_{n}=\sum _{i=1}^{n}{\vec {E}}_{i}=\sum _{i=1}^{n}{\frac {1}{4\pi \epsilon _{0}r^{2}}}{\vec {u_{r}}}_{i}$

注意这是一个矢量方程。因此必须使用矢量规则添加分量。

求偶极子的电场

1. 电偶极子是匹配的，相等但相反的电荷，以固定距离隔开。求偶极子的电场。对三种情况进行求解

a. 求偶极子电荷轴之间垂直的电场。求远场近似值。

b. 求偶极子电荷轴上的电场。将这种情况的远场近似值与上面的 a) 进行比较。

c. 求包含偶极子电荷的平面中垂直的电场

水分子。水分子由于电子在“弯曲”结构中的不均匀共享而具有电偶极矩。电荷在中间（红色阴影）有负电荷，在两端（蓝色阴影）有正电荷。

在物理学中，电偶极矩是衡量电荷系统中正负电荷分离的量度，即衡量电荷系统总极性的量度。它对于理解实际问题（如电容器的构造）非常重要。

求偶极子电荷轴之间垂直的电场

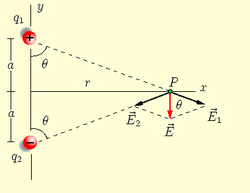图 1：电偶极子

为了确定由图 1 中以 2a 距离隔开的偶极子电荷产生的电场，我们只需将每个电荷单独产生的电场相加。注意电场是矢量。

${\vec {E}}={{\vec {E}}_{1}}+{{\vec {E}}_{2}}$

每个电荷（r）到测量电场点的距离是

$r={\sqrt {a^{2}+x^{2}}}$

第一个电荷（q₁）产生的电场（E₁）的大小和第二个电荷（q₂）产生的电场（E₂）的大小相同，尽管方向不同。

$E_{1}=E_{2}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{r^{2}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{a^{2}+x^{2}}}$

沿x轴方向的电场分量 $E_{1_{x}}$ 和 $E_{2_{x}}$ 大小相等，方向相反，相互抵消。

$E_{1_{x}}+E_{2_{x}}=0$

由于电场矢量的水平分量相互抵消，因此将 ${{\vec {E}}_{1}}$ 和 ${{\vec {E}}_{2}}$ 求和，就简化为将 $E_{1_{y}}$ 和 $E_{2_{y}}$ 求和。此外，垂直分量的幅度相同， $E_{1_{y}}=E_{2_{y}}$。由于 $\cos \theta ={\frac {adjacent}{hypotenuse}}$，求垂直分量就简化为

$E_{1_{y}}=E_{2_{y}}=E_{1}\cos \theta \,\!$ 或者：$E_{y}=2E_{1}\cos \theta \,\!$

但我们也知道

$\cos \theta ={\frac {a}{\sqrt {a^{2}+x^{2}}}}$

因此，我们可以将此代入 $E\,\!$ 的方程，得到

$E=2E_{1}\cos \theta \,\!={\frac {2}{4\pi \epsilon _{o}}}{\frac {q}{a^{2}+x^{2}}}{\frac {a}{\sqrt {a^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{o}}}{\frac {2aq}{(a^{2}+x^{2})^{\frac {3}{2}}}}$

在远离偶极子的区域，x远大于a (x>>a)。这通常被称为“远场”区域。我们可以通过提取x来找到场在远场区域的行为。

$E={\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{(a^{2}+x^{2})^{\frac {3}{2}}}}={\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{x^{3}}}{\frac {1}{(1+{({\frac {a}{x}})}^{2})^{\frac {3}{2}}}}$

通过观察，我们可以得出结论，当 x>>a 时，它将趋近于

$E\approx {\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{x^{3}}}$

对于某些分析来说，一个重要的问题可能是：远场近似在哪个范围内有效？我们可以通过使用二项式展开来找出答案（如果您需要，可以在本节的下一部分中复习二项式展开）。

$E={\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{(a^{2}+x^{2})^{\frac {3}{2}}}}={\frac {1}{4\pi \epsilon _{o}}}{\frac {2qa}{x^{3}}}{\frac {1}{(1+{({\frac {a}{x}})}^{2})^{\frac {3}{2}}}}$

我们将展开

${\frac {1}{(1+{({\frac {a}{x}})}^{2})^{\frac {3}{2}}}}$$=(1+{({\frac {a}{x}})}^{2})^{-{\frac {3}{2}}}=1-{\frac {3}{2}}{({\frac {a}{x}})}^{2}+...$

如果您只想在近似值引入的误差小于 1% 时使用它，那么——由于第一项是单位，您希望第二项小于单位的 1/100，或者

${\frac {1}{100}}>{\frac {3}{2}}{\left({\frac {a}{x}}\right)}^{2}$

${\frac {2}{300}}>{\left({\frac {a}{x}}\right)}^{2}$

${\sqrt {\frac {2}{300}}}>{\left({\frac {a}{x}}\right)}$

$x>{\sqrt {150}}\cdot a$

因此，如果 x 比 a 大 12.3 倍，则该近似值在 1% 内有效。

二项式展开复习

二项式展开复习

$\mathbf {(1+a)^{n}} =1+{\frac {n}{1!}}\cdot a+{\frac {n(n-1)}{2!}}\cdot a^{2}+{\frac {n(n-1)(n-2)}{3!}}\cdot a^{3}+...$

$\mathbf {(1+a)^{-{\frac {3}{2}}}} =1+{\frac {1}{1!}}\cdot {\frac {-3}{2}}\cdot a+{\frac {1}{2!}}\cdot {\frac {-3}{2}}\cdot {\frac {-5}{2}}\cdot a^{2}+{\frac {1}{3!}}\cdot {\frac {-3}{2}}\cdot {\frac {-5}{2}}\cdot {\frac {-7}{2}}\cdot a^{3}+...$

非正式来源链接

寻找偶极电荷形成的轴线上电场

图 2 - 计算偶极电荷线上电场的布局。

净电场是偶极电荷对电场的贡献之和。

${\vec {E}}={{\vec {E}}_{1}}+{{\vec {E}}_{2}}$

在解决任何问题时，首先应该做的事情是通过简单观察来考虑你所知道的事情。在本例中，电荷的大小和布局告诉我们一些事情。由于它们相等，并且我们知道点电荷的电场随 1/r² 衰减，因此我们知道最近的电荷将始终占主导地位。此外，我们还知道，在我们计算电场的轴线上，电场将没有垂直分量。

$E_{1_{y}}=E_{2_{y}}=0$

因此，现在我们将计算每个电荷在 x 方向上的电场大小：$E_{1_{x}}$ 和 $E_{2_{x}}$.

$E_{1}={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(r-a)}^{2}}}\qquad \qquad E_{2}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(r+a)}^{2}}}$

将向量大小$E_{1_{x}}$ 和 $E_{2_{x}}$ 相加

$E=E_{1_{x}}+E_{1_{x}}\,\!$

将上述方程代入，得到

$E={\frac {1}{4\pi \epsilon _{0}}}{\frac {q}{{(r-a)}^{2}}}+{\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(r+a)}^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{{(r-a)}^{2}}}-{\frac {q}{{(r+a)}^{2}}}\right]={\frac {1}{4\pi \epsilon _{0}}}\ 4aq\ {\frac {r}{{(r^{2}-a^{2})}^{2}}}$

2qa 的数量定义为偶极矩 (p)，因此我们可以代入

$p=2qa\,\!$

通过这种代入，我们现在得到

$E={\frac {1}{2\pi \epsilon _{0}}}{\frac {pr}{{(r^{2}-a^{2})}^{2}}}$

考虑远场情况（即 $r\,\!$ >> $a\,\!$ 的情况）

然后可以看出 $r^{2}\,\!$ >> $a^{2}\,\!$ 并且 $r^{2}-a^{2}\,\!$ 接近 $r^{2}\,\!$，这使我们能够简化远场中的方程。

$E={\frac {1}{2\pi \epsilon _{0}}}{\frac {p}{r^{3}}}$

请注意，可以使用二项式定理，就像上面的部分一样，找出该远场近似值（x>>a）的有效位置。

找到与平面上的任何地方的偶极子相关的电场

既然您已经解决了两种特殊情况，并确定偶极子场在很远距离处（称为远场）以 ${\frac {1}{r^{3}}}$ 的速度衰减，因此找到轴外场的行为很有启发性。

考虑一个电偶极子在点 $P\,\!$ 的场，该点的坐标为 $(x,y)\,\!$，如图所示。请注意，我们可以将坐标表示为笛卡尔坐标或圆柱坐标。

电偶极子在平面的场。

$r_{1}={\sqrt {{(y+a)}^{2}+x^{2}}}\quad \cos \alpha ={\frac {y+a}{\sqrt {{(y+a)}^{2}+x^{2}}}}\quad \sin \alpha ={\frac {x}{\sqrt {{(y+a)}^{2}+x^{2}}}}$

$r_{2}={\sqrt {{(y-a)}^{2}+x^{2}}}\quad \cos \beta ={\frac {y-a}{\sqrt {{(y-a)}^{2}+x^{2}}}}\quad \sin \beta ={\frac {x}{\sqrt {{(y-a)}^{2}+x^{2}}}}$

在笛卡尔坐标系中，可以按如下方式找到平面上任意点处每个电荷产生的电场：

${E_{r}}_{1}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}\quad {E_{r}}_{2}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}$

我们可以应用叠加原理并添加每个电荷产生的场，记住它们是矢量，因此垂直分量加到垂直分量，水平分量加到水平分量。

首先找到标记为 $E_{x}\,\!$ 的水平坐标。

${{E_{r}}_{1}}_{x}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}\sin \alpha ={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}{\frac {x}{\sqrt {{(y+a)}^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+qx}{{\left[{(y+a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}$

${{E_{r}}_{2}}_{x}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}\sin \beta ={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}{\frac {x}{\sqrt {{y-a)}^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-qx}{{\left[{(y-a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}}$

接下来找到标记为 $E_{y}\,\!$ 的两个电荷的垂直分量，我们得到

${{E_{r}}_{1}}_{y}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}\cos \alpha ={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q}{{(y+a)}^{2}+x^{2}}}{\frac {y+a}{\sqrt {{(y+a)}^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {+q(y+a)}{{\left[{(y+a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}$

${{E_{r}}_{2}}_{y}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}\cos \beta ={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q}{{(y-a)}^{2}+x^{2}}}{\frac {y-a}{\sqrt {{y-a)}^{2}+x^{2}}}}={\frac {1}{4\pi \epsilon _{0}}}{\frac {-q(y-a)}{{\left[{(y-a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}$

将水平分量相加得到

$E_{x}={\frac {1}{4\pi \epsilon _{0}}}q\left\lbrack {\frac {x}{{\left[{(y+a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}-{\frac {x}{{\left[{(y-a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}\right\rbrack$

对于大的 r（大的 x，大的 y 或者它们的组合），它变成

$E_{x}={\frac {qa}{2\pi \epsilon _{0}}}{\frac {1}{r^{3}}}$

将垂直分量相加得到

$E_{y}={\frac {1}{4\pi \epsilon _{0}}}q\left\lbrack {\frac {y+a}{{\left[{(y+a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}-{\frac {y-a}{{\left[{(y-a)}^{2}+x^{2}\right]}^{\frac {3}{2}}}}\right\rbrack$

求电四极子的电场

图 3 - 一种形式的电四极子

在垂直轴上某一点测得的电场，是由于水平轴上任何单个电荷产生的（如图 3 所示），

$E_{q}={\frac {q}{4\pi \epsilon _{o}r^{2}}}$

因此，中间的电荷贡献

$E_{2q}={\frac {2q}{4\pi \epsilon _{o}r^{2}}}$

而左、右电荷贡献的总电场大小为

$E_{-q}={\frac {-q}{4\pi \epsilon _{o}(r^{2}+d^{2})}}$

通过观察，我们可以看到电场的水平分量相互抵消。只剩下垂直分量。因此，我们乘以

$sin\theta ={\frac {r}{\sqrt {r^{2}+d^{2}}}}$

为了得到单个负电荷的电场垂直分量

$E_{-q}={\frac {-q}{4\pi \epsilon _{o}(r^{2}+d^{2})}}{\frac {r}{\sqrt {r^{2}+d^{2}}}}$

对于两个负电荷，我们得到

$E_{-2q}={\frac {-2q}{4\pi \epsilon _{o}(r^{2}+d^{2})}}{\frac {r}{\sqrt {r^{2}+d^{2}}}}$

现在我们可以加起来得到电场的总垂直分量。

$E=E_{2q}+E_{-2q}={\frac {2q}{4\pi \epsilon _{o}r^{2}}}+{\frac {-2q}{4\pi \epsilon _{o}(r^{2}+d^{2})}}{\frac {r}{\sqrt {r^{2}+d^{2}}}}$

简化为

$E={\frac {q}{2\pi \epsilon _{o}}}\left[{\frac {1}{r^{2}}}-{\frac {r}{{(r^{2}+d^{2})}^{\frac {3}{2}}}}\right]$

从分母的最后一项中提取 r³，得到

$E={\frac {q}{2\pi \epsilon _{o}}}\left[{\frac {1}{r^{2}}}-{\frac {r}{{r^{3}(1+({\frac {d}{r}})^{2})}^{\frac {3}{2}}}}\right]$

简化为

$E={\frac {q}{2\pi \epsilon _{o}r^{2}}}\left[1-{\frac {1}{{(1+({\frac {d}{r}})^{2})}^{\frac {3}{2}}}}\right]$

因此，我们现在有一个很好的方程式可以计算电场。工程师可能会认为这已经足够了，因为他们可以在需要的时候计算出数值，但物理学家想了解这个方程式在“远场” (r >> d) 的情况下是如何表现的。幸运的是，我们有一个工具——二项式展开式——可以帮助我们解答远场的问题，如下所示

$\left[1-{\frac {1}{{(1+({\frac {d}{r}})^{2})}^{\frac {3}{2}}}}\right]=\left[1-{{\left(1+\left({\frac {d}{r}}\right)^{2}\right)}^{-{\frac {3}{2}}}}\right]=\left[1-\left(1-{\frac {3}{2}}\left({\frac {d}{r}}\right)^{2}\right)+...\right]={\frac {3}{2}}\left({\frac {d}{r}}\right)^{2}$

将该结果代回原方程式中

$E={\frac {q}{2\pi \epsilon _{o}r^{2}}}{\frac {3}{2}}\left({\frac {d}{r}}\right)^{2}$

简化后，我们发现，在远场 (r >> d) 中，四极子的电场随 ${\frac {1}{r^{4}}}$ 衰减。

$E={\frac {3qd^{2}}{4\pi \epsilon _{o}r^{4}}}$

与线电荷相关的电场

1. 一个非常长的固体非导电圆柱体，半径为R₀，长度为L（R₀ << L），具有均匀的体积电荷密度ρ_E（C/m³）。对于远离两端的点，且r << L，
   1. 求所有r的电场，r为距圆柱体轴线的距离。您可能需要分别针对r < R₀和r > R₀给出表达式。证明电场在r = R₀处是连续的，即电场的两个表达式在r = R₀处一致。
   2. 描述一个位于圆柱体内的小自由电荷Q（符号相反，即Q ρ_E < 0）的运动。求电荷绕圆柱体轴线振荡的频率$\nu$。（注意：$\nu$，频率，单位为赫兹，而$\omega$，角频率，单位为弧度/秒。）
   3. 让我们改变一下问题，假设我们有一个圆柱形电荷壳（半径为R₀，σ_E，使得总电荷保持不变）。r < R₀或r > R₀区域的电场表达式如何变化？电场仍然连续吗？给出合理的论据解释为什么我们可能不期望电场是连续的。

求具有均匀线电荷密度λ库仑/米的有限线的电场

具有均匀线电荷密度的无限长直线。

图示了具有线性电荷密度$\lambda \,\!={\frac {dq}{dx}}$的有限长直线电荷。电荷从x = -a延伸到x = +b，它们是任意的（虽然不是无限的），在图中没有显示。

与无限长直线的推导一样，该直线电荷的一小段dx在点P处产生的电场大小是电荷$dq=\lambda dx\,\!$产生的结果。

有了这个电荷，我们可以计算dq对P点的场贡献（dE）为

$dE={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {dq}{r^{2}}}={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}$           (1)

我们不能再根据对称性来论证电场在距无限长直线电荷等距的任何点都相同，因此我们可以详细地解决这个问题，我们将使用二维来解决。一旦我们获得了二维的解，围绕直线电荷的简单旋转将使我们能够确定第三维的场。

电场是一个向量，我们将用$d{\vec {E}}$来表示。我们将将其分解为二维笛卡尔坐标系中的分量

$dE_{x}=-dE\sin \theta \,\!$      和      $dE_{y}=dE\cos \theta \,\!$

电场在$dE_{x}\,\!$ 处的符号表示点相对于x轴的$d{\vec {E}}_{x}$ 位置。

我们可以通过积分来求出水平方向上的总电场$E_{x}$ 和垂直方向上的总电场$E_{y}$，从而确定点P处的${\vec {E}}$。注意$\sin \theta$ 用于求水平方向上的电场分量，而$\cos \theta$ 用于求垂直方向上的电场分量。

$E_{x}=\int dE_{x}=-\int _{x=-a}^{x=+b}\sin \theta \,dE$

以及

$E_{y}=\int dE_{y}=\int _{x=-a}^{x=+b}\cos \theta \,dE$

或者用完整的矢量形式

${\vec {E}}=\int _{L}\,d{\vec {E}}=\int _{L}{\frac {1}{4\pi \epsilon _{0}}}{\frac {dq}{r^{2}}}{\vec {u_{r}}}=\int _{L}{\frac {1}{4\pi \epsilon _{0}}}{\frac {\lambda dx}{r^{2}}}{\vec {u_{r}}}$

在这个例子中，从电荷到点P的距离r可以用直角坐标x和y表示。

$r={\sqrt {x^{2}+y^{2}}}$.

这使我们能够使用以下公式计算点 P 上由电荷 dx 在 r 处产生的电场的强度：$dE={\frac {1}{4\pi {\epsilon }_{0}}}={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}$

$\sin \theta ={\frac {opposite}{hypotenuse}}={\frac {x}{\sqrt {x^{2}+y^{2}}}}$          以及         $\cos \theta ={\frac {adjacent}{hypotenuse}}={\frac {y}{\sqrt {x^{2}+y^{2}}}}$

然而，我们必须记住，该强度对应于向量$d{\vec {E}}$，它随着沿着线的移动而变化。因此，我们必须找到$d{\vec {E}}$在 x 方向或 y 方向上的分量。

为了找到 x 方向上的分量$dE_{x}=-dE\sin \theta \,\!$，为了找到 y 方向上的分量，应用$dE_{y}=dE\cos \theta \,\!$。

场在 x 方向上的分量$d{\vec {E}}_{x}$可以通过从线源的一端 -a 积分到另一端 a 来找到。如果线源在左右两侧长度相等，则 x 方向上的净场将如以下所示抵消。

$E_{x}=\int dE_{x}=-\int _{x=-a}^{x=+b}\sin \theta \,dE=-\int _{x=-a}^{x=+b}{\frac {x}{\sqrt {x^{2}+y^{2}}}}\,dE$

$E_{x}=\int _{x=-a}^{x=+b}{\frac {x}{\sqrt {x^{2}+y^{2}}}},{\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}$        (2)

$E={\frac {\lambda }{4\pi {\epsilon }_{0}}}\int _{x=-a}^{x=+b}{\frac {xdx}{\left[{x^{2}+y^{2}}\right]^{\frac {3}{2}}}}$           (3)

$E_{x}={\frac {\lambda }{4\pi {\epsilon }_{0}}}\left[-{\frac {1}{\left[a^{2}+y^{2}\right]^{\frac {1}{2}}}}+{\frac {1}{\left[b^{2}+y^{2}\right]^{\frac {1}{2}}}}\right]$        (4)

保持 1

类似地，场 $d{\vec {E}}_{y}$ 的 y 分量可以通过从直线源的一端 -a 积分到另一端 a 来找到。

$E_{y}=\int dE_{y}=\int _{x=-a}^{x=+b}\cos \theta \,dE=\int _{x=-a}^{x=+b}{\frac {y}{\sqrt {x^{2}+y^{2}}}}\,dE$

代入上式，得到

$E_{y}=\int _{x=-a}^{x=+b}{\frac {y}{\sqrt {x^{2}+y^{2}}}}\,{\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}={\frac {\lambda y}{4\pi {\epsilon }_{0}}}\int _{x=-a}^{x=+b}{\frac {dx}{\left[x^{2}+y^{2}\right]^{\frac {3}{2}}}}$        (5)

$E_{y}={\frac {\lambda y}{4\pi {\epsilon }_{0}}}\int _{x=-a}^{x=+b}{\frac {dx}{\left[x^{2}+y^{2}\right]^{\frac {3}{2}}}}$        (6)

$E_{y}={\frac {\lambda }{4\pi {\epsilon }_{0}y}}\left[{\frac {x}{\left[x^{2}+y^{2}\right]^{\frac {1}{2}}}}\right]_{x=-a}^{x=+b}$        (7)

求单位长度电荷量为 λ 库仑的无限长直线的电场

具有均匀线电荷密度的无限长直线。

图中显示了一条无限长的线状电荷，其线性电荷密度为 $\lambda \,\!={\frac {dq}{dx}}$.

在点 P 处测量到的由这条线状电荷的一小段 dx 产生的电场的强度，是电荷 $dq=\lambda dx\,\!$ 的结果。

有了这个电荷，我们可以计算dq对P点的场贡献（dE）为

$dE={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {dq}{r^{2}}}={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}$           (1)

由于我们可以通过对称性来论证，电场在与无限长直线电荷等距的任何点上都是相同的，因此我们可以用二维来求解这个问题。一旦我们得到了二维的解，围绕线状电荷的简单旋转就可以提供三维的场。

电场是一个向量，我们将用$d{\vec {E}}$来表示。我们将将其分解为二维笛卡尔坐标系中的分量

$dE_{x}=-dE\sin \theta \,\!$      和      $dE_{y}=dE\cos \theta \,\!$

电场在$dE_{x}\,\!$ 处的符号表示点相对于x轴的$d{\vec {E}}_{x}$ 位置。

我们可以通过积分来求出水平方向上的总电场$E_{x}$ 和垂直方向上的总电场$E_{y}$，从而确定点P处的${\vec {E}}$。注意$\sin \theta$ 用于求水平方向上的电场分量，而$\cos \theta$ 用于求垂直方向上的电场分量。

$E_{x}=\int dE_{x}=-\int _{x=-\infty }^{x=+\infty }\sin \theta \,dE$

以及

$E_{y}=\int dE_{y}=\int _{x=-\infty }^{x=+\infty }\cos \theta \,dE$

在这些表达式中，$E_{x}\,\!$ 必须积分到零，因为垂直点 P 左侧的每个电荷元素都有一个在右侧的对应元素，因此它们对水平方向的场贡献相互抵消。所以 ${\vec {E}}$ 仅指向垂直方向。至于对 $E_{y}\,\!$ 的电场贡献，带电线的右半部分和左半部分将做出相同的贡献，所以我们可以写成

$E=E_{y}=2\int _{x=0}^{x=+\infty }\cos \theta \,dE$

将上面的式子 (1) 代入这个方程，我们得到

$E=2\int _{x=0}^{x=+\infty }\cos \theta \,{\frac {1}{4\pi {\epsilon }_{0}}}{\frac {\lambda dx}{x^{2}+y^{2}}}={\frac {\lambda }{2\pi {\epsilon }_{0}}}\int _{x=0}^{x=+\infty }\cos \theta \,{\frac {dx}{x^{2}+y^{2}}}$          (2)

根据定义，$\tan \theta ={\frac {x}{y}}$，我们可以写成$x=y\tan \theta \,\!$。对该表达式求导，得到：$dx=y{\sec }^{2}\theta d\theta \,\!$。将此代入 (2)，得到

$E={\frac {\lambda }{2\pi {\epsilon }_{0}}}\int _{x=0}^{x=+\infty }\cos \theta \,{\frac {y{\sec }^{2}\theta d\theta }{x^{2}+y^{2}}}={\frac {\lambda }{2\pi {\epsilon }_{0}}}\int _{x=0}^{x=+\infty }{\frac {y}{x^{2}+y^{2}}}\cos \theta {\sec }^{2}\theta d\theta$      (3)

应用更多三角关系：$\cos \theta ={\frac {y}{r}}$，   $\sec \theta ={\frac {r}{y}}\quad$    以及    $\quad x^{2}+y^{2}=r^{2}\,\!$，    我们可以建立等价关系

${\frac {y}{x^{2}+y^{2}}}\cos \theta {\sec }^{2}\theta d\theta ={\frac {y}{r^{2}}}{\frac {y}{r}}{\frac {r^{2}}{y^{2}}}={\frac {y}{ry}}={\frac {\cos \theta }{y}}$

这可以代入公式 (3) 以得到一个简化的积分

$E={\frac {\lambda }{2\pi {\epsilon }_{0}y}}\int _{x=0}^{x=+\infty }\cos \theta d\theta$

为了评估这一点，我们只需要观察到 $x\rightarrow 0\,\!$，$\theta \rightarrow 0\,\!$，类似地 $x\rightarrow +\infty \,\!$，$\theta \rightarrow {\frac {\pi }{2}}\,\!$，以简化我们的积分范围为

$E={\frac {\lambda }{2\pi {\epsilon }_{0}y}}\int _{\theta =0}^{\theta ={\frac {\pi }{2}}}\cos \theta d\theta ={\frac {\lambda }{2\pi {\epsilon }_{0}y}}{\Bigg [}\sin {\frac {\pi }{2}}-\sin 0{\Bigg ]}={\frac {\lambda }{2\pi {\epsilon }_{0}y}}$

这得出一个最终的解

$E={\frac {\lambda }{2\pi {\epsilon }_{0}y}}$

这可以推广到距离线电荷 r 的任何点

$E={\frac {\lambda }{2\pi {\epsilon }_{0}r}}$