物理教科书/光
光是电磁辐射,波长范围在人眼可见范围内,或者更广义地说,是指从红外到紫外范围内的任何电磁辐射。光的三个基本维度(以及所有电磁辐射)是
- 强度(或亮度或振幅,人类感知为光的亮度),
- 频率(或波长,人类感知为光的颜色),以及
- 偏振(或振动角度,在普通情况下,人类无法感知)
由于波粒二象性,光同时表现出波和粒子的性质。
解释光本质的现代理论是波粒二象性,由阿尔伯特·爱因斯坦在20世纪早期基于他对光电效应和普朗克结果的研究而提出。爱因斯坦确定光子的能量与其频率成正比。更一般地,该理论指出,任何事物都具有粒子性和波动性,可以通过不同的实验来展现其中的一种或另一种性质。如果一个物体具有很大的质量,那么它的粒子性更容易被辨别,因此直到路易·德布罗意在1924年进行的实验,人们才意识到电子也表现出波粒二象性。爱因斯坦因其在光子波粒二象性方面的工作获得了1921年的诺贝尔奖,德布罗意则因将这一理论扩展到其他粒子而在1929年获得了诺贝尔奖。
人眼检测到不同的波长,然后由人脑解释为颜色,从最长波长(最低频率)的红色到最短波长(最高频率)的紫色。中间频率被视为橙色、黄色、绿色、蓝色和传统意义上的靛蓝色。

电磁频谱中人眼无法看到/检测到的范围以外的波长被称为紫外线(UV),在短波长(高频率)端,以及红外线(IR),在长波长(低频率)端。虽然人类无法看到IR,但我们确实可以通过皮肤上的感受器来感知近红外(更短波长、更高频率、更高能量)作为热量。能够检测红外线并将其转换为光的相机被称为夜视相机。
人类无法感知紫外线辐射,除了以非常延迟的方式,因为皮肤过度暴露于紫外线会导致晒伤或皮肤癌。一些动物,如蜜蜂,可以看到紫外线辐射,而另一些动物,如响尾蛇,可以使用头上的热感应器来感知红外线。
在研究折射、镜子和透镜时,我们忽略了光的波动性。
光既表现为波,也表现为粒子射线。当观察光对大型物体(如玻璃立方体、镜子和透镜)的影响时,光可以被观察到像一束微小的粒子一样,可以被反射、引导或减速。
介质减慢光速——割草机类比
镜子反射光——会聚镜、发散镜
透镜引导光——会聚透镜、发散透镜


折射是指由于速度变化而导致的波方向改变。当波从一个具有特定折射率的介质传播到另一个具有不同折射率的介质时,就会发生这种情况。在介质边界处,波会改变方向;它的波长会增加或减少,但频率保持不变。例如,光线通过玻璃时会发生折射;对这一概念的理解导致了折射望远镜的发明。
在右侧的图中,波纹从左侧传播,并穿过一个以一定角度倾斜的更浅区域。波纹在更浅的水中传播速度更慢,因此波长减小,波在边界处弯曲。虚线表示边界法线。虚线表示波纹的原始方向。这种现象解释了为什么海边的波纹永远不会以一个角度撞击海岸线。无论波纹在深水中以何种方向传播,它们在进入靠近海滩的浅水区时总是朝向法线方向折射。
一个例子就是往水盆里看。空气的折射率约为1.003,水的折射率约为1.33。如果你看一个直的物体,比如铅笔,斜着放在水中,物体看起来会在水面上弯曲。这是因为来自物体的光线在从水中进入空气时发生弯曲。这使得水看起来比实际的要浅。
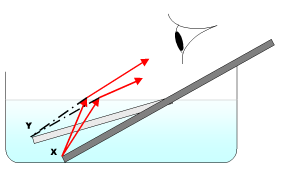
在图中,深色矩形表示一根放在水盆中的铅笔的实际位置。浅色矩形表示铅笔的视觉位置。请注意,末端 (X) 看起来像在 (Y) 处,这个位置明显比 (X) 浅。
折射也是彩虹形成的原因,也是白光通过玻璃棱镜时分解成彩虹光谱的原因。玻璃的折射率高于空气,不同频率的光速不同(色散),导致它们以不同的角度折射。不同的频率对应着观察到的不同颜色。
光线在折射过程中弯曲的程度可以使用斯涅尔定律计算。
最近,一些具有负折射率的超材料被创造出来。
频率是基础
光速永远不会改变。
光的频率和波长 (λ) 会发生变化。

频率是衡量重复事件在单位时间内发生次数的量。要计算频率,需要固定一个时间间隔,计算该时间间隔内事件发生的次数,然后将该计数除以时间间隔的长度。
在 SI 单位中,结果以赫兹 (Hz) 为单位,以纪念德国物理学家海因里希·鲁道夫·赫兹。1 Hz 表示事件每秒重复一次。其他用于测量频率的单位包括:每秒周期数、每分钟转数 (rpm)。
测量电磁波(如光)的频率,以赫兹为单位,指的是每秒重复波形的循环次数。如果波是声音,频率决定了它的音调。
频率与波长之间存在反比关系。频率 f 等于波的速度 v 除以波长 λ(lambda)。
在电磁波在真空中传播的特殊情况下,v = c,其中 c 是光在真空中的速度,这个表达式就变成了:
注意:记住f=f 当波从一种介质传播到另一种介质时,它们的频率基本保持不变,只有波长发生变化。
要了解光如何穿过介质(如玻璃),可以使用一个人骑着自走式割草机的类比。
当这个人走在草地上时,他们会打滑并缓慢移动。当他们走到水泥地上时,他们不再打滑,速度加快了。割草机在草地上移动就像光在介质(如玻璃)中移动一样,割草机在水泥地上移动就像光在真空中移动一样。
此外,当割草机在水泥地上移动并以一定角度撞击草地时,割草机的一个前轮会撞到草地并短暂减速,而另一个前轮会保持相同速度。这改变了割草机方向。就像一束光从真空中进入介质(如玻璃)时,当它撞击介质时会改变方向。光线会朝垂直方向弯曲。
斯涅尔定律是一个简单的公式,用于计算光在不同折射率的两种介质之间传播时的折射。它以其发现者荷兰数学家威勒布罗德·斯涅尔(1580-1626)命名。

在右侧的图中,两种折射率分别为 n1(左侧)和 n2(右侧)的介质在一个表面或界面(垂直线)处相遇。n2 > n1,光在第二种介质中的相速度较慢。
左侧介质中的一束光线 PO 在点 O 处入射到界面。从点 O 开始,我们垂直于界面投影一条直线;这被称为表面的法线(水平线)。法线与入射光线 PO 之间的角度被称为入射角,θ1。
光线穿过界面进入右侧的介质;这显示为光线 OQ。它与法线所成的角度被称为折射角,θ2。
斯涅尔定律给出了 θ1 和 θ2 之间的关系
注意,对于 θ1 = 0°(即垂直于界面的射线)的情况,解为 θ2 = 0°,无论 n1 和 n2 的值如何。换句话说,垂直于表面的入射射线永远不会发生弯曲。
以上内容对于光从稠密介质到稀疏介质的传播也适用;斯涅尔定律的对称性表明,相同的射线路径在相反方向上适用。
确定折射方向的一个定性规则是,稠密介质中的射线总是更靠近法线。记住这一点的一个简便方法是,想象一下一辆汽车越过沥青(稀疏介质)和泥土(稠密介质)之间的边界。根据角度的不同,汽车的左轮或右轮会先越过新介质,导致汽车转向。
当从稠密介质到稀疏介质移动时(即 n1 > n2),很容易验证,当 θ1 超过一个称为临界角的值时,上述方程没有解。
当 θ1 > θcrit 时,没有折射光线出现,入射光线在界面处发生全内反射。
给定一个归一化的射线向量 v 和一个归一化的平面法向量 p,可以计算出归一化的反射和折射射线:(注意实际角度 θ1 和 θ2 没有计算出来)
这些余弦值可以重复使用,并用于菲涅耳方程,计算所得光线的强度。在全内反射时,平方根会变成虚数,折射光线不再是真实的(显然存在某种形式的折射光线,但它衰减非常快,呈指数级随距离增加而衰减)。
斯涅尔定律可以从费马原理推导出来,费马原理指出光线遵循最短时间路径传播。通过对光程长度求导,可以找到驻点,从而得到光线传播的路径。在费曼的经典类比中,低折射率区域被替换为沙滩,高折射率区域被替换为海洋,沙滩上的救援人员最快到达海里溺水者的方式是沿着遵循斯涅尔定律的路径奔跑。








