地球/1e. 地球的运动和自转

地球
1e. 地球的运动和自转

地球每天的自转

现在，当你阅读这篇文章时，你的身体正以极快的速度穿越外太空。我们可以通过地球的周长来计算这种速度的一个分量，地球周长基于地球尺寸的椭圆模型，其赤道周长为 24,901.46 英里 (40,075.02 公里)。地球每天绕其轴旋转一次，更准确地说，每 23 小时 56 分钟 4 秒旋转一次。如果你位于赤道，你的速度（速度加上方向）可以通过将 24,901.46 英里除以 23 小时 56 分钟 4 秒来计算，等于每小时 1,040.45 英里。当然，这取决于你的纬度，随着你接近两极，速度会降低。

想象这种旋转的一种方式是，如果你曾经看过一个老式的黑胶唱片旋转，或者一个自由旋转的自行车轮子。旋转的唱片或轮子的中心轴是静止的，而圆形的外缘在每次旋转时都会以圆形的周长移动，你离旋转中心越远，你的速度就越快。换句话说，轮子越大，旋转速度越快，单位时间内覆盖的距离就越多。

早期的科学家，如伽利略，意识到了这种运动，并且很好奇为什么我们在地球表面上感觉不到这种运动。如果你想象一只蚂蚁在一个旋转的唱片上爬行，在边缘，蚂蚁会感觉到快速的运动，因为空气呼啸而过，并且感觉到一种离心力，试图将可怜的蚂蚁从旋转的唱片上甩出去，但当蚂蚁向中心爬行时，它的运动感会减弱。

如果你曾经玩过旋转木马，你也会感觉到同样的情况，你离中心越近，你感觉到的旋转运动就越少。然而，在地球上，我们感觉不到我们在赤道上以每小时 1,000 英里的速度行进，也感觉不到站在北极或南极附近是静止的。

这种奇怪的悖论激发了艾萨克·牛顿研究运动，并在此过程中发现了万有引力和牛顿运动定律，它支配着宇宙中所有物体的运动。他的发现发表在 1687 年的《自然哲学的数学原理》(自然哲学的数学原理) 中。

在我们讨论为什么我们感觉不到地球的自转力之前，我们需要定义一些术语。

速度: 是物体在一定时间内运动的距离。例如，一辆汽车的速度可能为每小时 50 英里（每小时 80.5 公里）。
速度: 是速度加上空间方向。
加速度: 是速度变化率。例如，如果一辆汽车以每小时 50 英里的速度行驶 50 英里，并且没有改变速度，那么它的加速度为 0。一辆静止不动且没有移动的汽车也具有 0 加速度（在相应的参考系中）。这是因为在这两个例子中，速度都没有改变。

从数学上讲，计算加速度更困难，一种方法是找到每个时间单位的速度变化。例如，一辆汽车在 5 小时的赛道上从 0 加速到每小时 50 英里，我们可以找到每 1 小时间隔的速度并对其进行平均。

在起跑线上，汽车的速度为每小时 0 英里。1 小时后，汽车的速度为每小时 10 英里。2 小时后，汽车的速度为每小时 20 英里。3 小时后，汽车的速度为每小时 30 英里。4 小时后，汽车的速度为每小时 40 英里。5 小时后，汽车的速度为每小时 50 英里。每小时，汽车的速度都会增加每小时 10 英里。

因此，平均加速度等于速度的平均变化量除以时间的平均变化量，在本例中，平均值为 10、10、10、10、10。平均加速度等于每小时 10 英里，每小时（或每小时平方）。

如果你懂一些微积分，我们可以找到所谓的瞬时加速度，或者使用以下公式找到加速度

\mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}

基本上，这个方程表明加速度是速度对时间的导数。

艾萨克·牛顿认为，我们在地球上感觉不到这种旋转运动的原因是地球自转的速度是恒定的。那些被设定为运动并且具有恒定速度的物体被称为具有惯性。这些物体的加速度为零。

加速度是速度随时间变化的情况。艾萨克·牛顿意识到，运动的物体将保持运动状态，除非受到其他力的作用。这被称为惯性定律。在外太空的失重环境中，宇航员可以旋转篮球，它将继续以该速度旋转，除非它撞到另一个物体，或者另一个物体对该运动起作用。我们感觉不到地球自转的原因是，所有物体都以这种恒定速度旋转，或者表现出相同的惯性力。

然而，正如艾萨克·牛顿意识到的那样，你应该感觉到由于这种旋转力而产生的离心力。力是任何导致物体沿某个方向移动的相互作用。

牛顿提出了一个简单的问题，为什么像苹果这样的物体掉落到地球上，而不是由于地球的自转而被甩到外太空呢？

他开始测量坠落物体的加速度。例如，从塔上掉下来的球。在球掉下来之前，它的速度是每秒 0 米，但在 1 秒后，球的速度是每秒 10 米。在 2 秒时，球的速度是每秒 20 米。在 3 秒时，球的速度是每秒 30 米。在 4 秒时，球的速度是每秒 40 米。在 5 秒时，球的速度是每秒 50 米。这听起来很熟悉。每秒球的速度都会增加 10 米/秒。所以，坠落物体的加速度是每秒 10 米/秒（或平方秒）或 10 m/sec²。

一个世纪的实验表明，地球表面上的坠落物体的加速度为 9.8 m/sec²。所有物体，无论它们的质量如何，都会以这种速度下降。

（实际上，物体在坠落时会撞击空气（气体），运动中的物体将保持运动状态，直到被另一个物体撞击，在这种情况下是“空气”粒子。这种空气在自由落体过程中会增加阻力。因此，像降落伞这样的物体，它们很宽，很宽，并且在坠落时会捕捉到大量的空气，或者羽毛会下降得更慢。然而，9.8 m/sec² 的标准加速度仍然相同，但阻力会抵消这种力）。

坠落物体的力与质量和加速度都有关。

力由质量（以千克为单位测量）乘以加速度（以米每平方秒为单位测量）来衡量。艾萨克·牛顿因为以他命名的测量单位而获得奖励！

一个牛顿力的单位等于 1 千克 x 1 m/sec²。

因此，一个质量为 5 千克的保龄球将施加 5 千克 x 9.8 m/s² 或 49 牛顿的力。一个质量为 2 千克的海滩球将施加 2 千克 x 9.8 m/s² 或 19.6 牛顿的力。以牛顿为单位的物体是重量，因为重量包含质量和加速度。单位磅（磅）也是重量单位。

这种地球表面常见的加速度是重力加速度，为 9.8 m/sec²。艾萨克·牛顿意识到有一种力作用于物体使其保持在地球表面，并且该力与地球的质量直接相关。物体的质量越大，它的重力就越大。它也与物体的距离相关，物体越靠近，它受到的重力加速度就越大。利用这种数学关系，牛顿提出 9.8 m/sec² 的重力加速度可以用来计算地球的质量，使用此公式。

g={\frac {GMe}{re^{2}}}

g = 9.8 m/sec²，是地球表面的重力加速度。

re = 地球的半径，或从地球中心到表面的距离，如果我们知道地球的周长就可以找到它。

Me = 地球的质量，以千克为单位测量。

G = 万有引力常数，“有时称为大 G”，是一个常数，单位为 m³/kg ⋅s²。

质量 = 密度 x 体积。密度是指物质的紧密程度，相对于另一种物质（如水）进行测量。换句话说，密度是指物质或物体漂浮或沉没的程度。体积是指物体占据的立方尺寸或空间。

艾萨克·牛顿并不知道大 G（万有引力常数）的值，但他知道它是一个很小的数字，因为地球的质量和半径非常大，而方程的结果必须等于 9.8 m/sec²。

寻找大 G 的探索

牛顿的工作促使新一代科学家试图确定大 G，即万有引力常数。确定大 G 的一种方法是确定地球的密度、体积和半径。我们可以使用此公式求解大 G，

G={\frac {gr^{2}}{DV}}

其中 g 是地球上的重力加速度，r 是从地球中心到表面的地球半径，D 是地球密度，V 是地球的体积。

艾萨克·牛顿的同事之一是埃德蒙·哈雷。哈雷是当时最杰出的科学家之一，他以计算彗星的周期性而闻名，事实上哈雷彗星以他的名字命名。然而，他不太以他关于地球是空心的的假设而闻名。他提出，地球的密度，因此是质量，比地球由非常致密的固体内核组成要小得多。在 17 世纪后期和 18 世纪初，科学家们争论地球的密度是多少。牛顿提出平均密度大约是水的 5 倍，而哈雷提出地球内部的平均密度小于水。问题是没有人知道大 G 的值。

在接下来的一个世纪里，关于地球密度（D 的值）的讨论很多。探险队前往世界各地的洞穴和黑暗洞穴，试图找到通往传说中地球空心中心的入口。这场争论引起了一个小个子名叫约翰·米歇尔的人的兴趣，他是英国约克郡一家教堂的主持人，但他闲暇时会涉足科学，并经常给当时的科学家（包括本杰明·富兰克林）写信。在他闲暇时，他想出一个实验来测量大 G，方法是使用一组放在非常接近一组悬挂在连接到平衡杆的绳索上的较小但也非常致密的铅球的非常致密的铅球。当大铅球放在小铅球旁边时，重力会使两个球相互吸引。这种吸引力会导致平衡杆略微移动。为了测量这种移动或平衡杆角度的变化，一束光被反射到放在平衡杆顶部的镜子。知道铅球的质量和半径，就可以求解万有引力常数，即大 G，如果已知，就可以用来确定地球的密度。

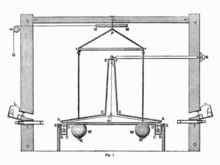
约翰·米歇尔的一位亲密朋友是亨利·卡文迪许，一位出身名门望族的富裕科学家的儿子。亨利患有今天被称为自闭症的疾病，因为他非常害羞，而且很难与除他亲密朋友以外的人交谈。后来，在 68 岁时，约翰·米歇尔去世，并将他的实验留给了亨利·卡文迪许来完成。在一栋大楼里，亨利重建了这个实验，将铅球放在他家附近，并计算出了大 G（万有引力常数）的精确测量值，即 6.674×10−11 m³/kg⋅s²。

使用这个大 G 的数字，证明了地球不是空心的，实际上，它比地球表面附近的岩石密度更大，岩石密度约为 3 g/cm³，平均密度为 5.51 g/cm³，是水的 5.5 倍。这证明了地球内部不是空心的，而是比在地球表面发现的普通岩石密度要大得多。

亨利·卡文迪许精确计算了万有引力常数，使你能够计算任何物体的重力加速度，只需要知道它的质量和距其质量中心的半径。物体质量、半径和重力加速度之间的关系是理解地球运动的基本概念，不仅包括地球，还包括其他行星、卫星和恒星。以及相互作用的星体之间的引力。此外，它还解释了为什么宇宙中的大型物体在质量中心周围呈现球形。重力加速度也解释了为什么我们感受不到地球的自转，为什么地球上的物体和物质不会被甩到外太空。它们被地球的引力吸引着。

地球会停止自转吗？

你是否担心地球的自转速度会减慢，或者将来有一天地球会停止自转？

一天的长度是地球自转一周的时间，在这期间，每个经度线都只面向太阳一次。如果地球的自转速度随着时间的推移而减慢，一天的长度就会增加，导致白天和黑夜变长。如今，地球完成一次自转需要23小时56分钟4.1秒。（注意，太阳精确地需要24小时才能到达每天天空中的最高点，这比地球的自转时间略长，因为地球每天相对于太阳移动一点点。）

当然，白天和黑夜的时长会根据你的位置和时间而变化，因为地球绕着极轴自转，而极轴相对于太阳倾斜了23.5°。这就是为什么阿拉斯加（纬度较高）的人在7月份经历的白天比赤道附近的人更长，而在12月份经历的黑夜更长。需要问的问题是，地球的自转速度是否一直保持在23小时56分钟4.1秒？

就像一个旋转的陀螺，地球的自转速度可能正在减慢。测量地球每次自转的时长需要每天用一个非常精确的秒表点击，并记录地球完成一次自转所需的时间。在大多数情况下，它保持在23小时56分钟4.1秒左右。然而，时长确实会有大约4到5毫秒的波动。换句话说，每天会增加或减少0.004到0.005秒。这些波动似乎以十年的周期出现，因此1860年代的白天比1920年代的白天短了0.006秒。这些十年的波动被认为是地球流体外核和周围固体地幔之间角动量传递的结果，以及海洋潮汐摩擦力在自转的地球表面来回移动时产生的摩擦力。每年都会出现较弱的波动，6月、7月和8月的白天比12月、1月和2月的白天短了0.001秒。这些较弱的波动是由于大气和海洋摩擦力造成的，当地球自转时，会产生一种叫做 “钱德勒摆动” 的振荡，以美国科学家S. C. 钱德勒命名。事实上，地球不仅仅是一个固体岩石，我们还有液态海洋和气态大气，它们会影响每一天的长度。就像你在一个装满湿衣服的洗衣机里旋转，根据衣服在每个旋转周期的位置，旋转本身的速度会有所不同。

气候变化也会对一天的长度产生相当重要的影响。如果我们将最近一次冰川期（25000年前）的平均日长与今天进行比较，我们会发现当时的日长更短。这是因为地球的极地惯性矩减小了。当覆盖极地大部分地区的巨大极地冰盖开始融化时，地球的质量分布从靠近旋转星球中心的极地地区（作为冰盖）转移到赤道地区（作为融化的海水）。这种惯性矩的变化与你在溜冰者在旋转过程中伸出手臂时观察到的现象相同。旋转速度会减慢。因此，随着地球巨大的冰盖在过去25000年中融化，地球就像旋转的溜冰者一样，将更多质量从中心向赤道外抛出，导致自转速度减慢。

虽然这些波动很有趣，但它们很小（几毫秒），但我们想知道地球何时会停止自转，为了这个问题，我们需要更长时间的日长记录，追溯到数百万年前。

化石生物记录了地球过去数百万年的每一年、每个月和每一天的长度。生活在海洋潮间带的化石珊瑚会受到地球自转和月球引力造成的两次潮汐的影响，太阳的相对位置也会放大这种影响。这些水深变化会在生长环中留下记录，以及循环沉积物，例如潮汐节律岩和条带状铁建造。利用这些信息，地球的自转速度每百万年增加了15.84秒。

艾萨克·牛顿提出，运动中的物体将保持运动状态，除非受到其他力的作用。那么是什么力量减缓了地球的自转速度呢？

答案是我们的近邻——月球！

月球是地球唯一的天然卫星，赤道周长为10921公里（或6786英里），大约是地球的27%。它每27.32天绕地球运行一个朔望月，以一种叫做同步自转的不寻常轨道运行。这导致了奇怪的事实：月球始终保持几乎相同的一面或表面朝向地球。你从地球上在夜空中看不到的月球背面错误地被称为月球的“黑暗面”。

两侧都每隔29.5个地球日被照亮一次，因为月球绕地球自转，导致太阳照亮月球的不同阶段。月球自转轴相对于太阳的倾斜角度仅为5.14°，并且由于地球的自转而减慢，最终与地球“潮汐锁定”。

随着月球绕地球运行的较慢的朔望月自转，它就像一个缓慢的刹车作用于地球的自转。地球会减速以匹配月球绕地球运行的27.32天或559.68小时的轨道。到那时，地球的自转速度将与月球绕地球运行的轨道锁定。

如果地球的自转周期与现在的朔望月相同，那么地球上的白天将持续27.32天，导致白天和黑夜的温度极端，就像今天在月球表面一样！这是你需要担心的事情吗？

不用担心，地球的自转速度被月球减慢了每百万年仅仅几秒，因此，直到1210亿年后，地球才会与月球锁定在这样的死亡轨道上，到那时，地球和月球可能已经被膨胀的太阳吞噬了！

月球绕地球运行的影响可以通过观察海洋潮汐的变化来观察。当月球直接位于地球上的某个位置（地心）时，由于月球的引力作用，该位置的海洋会被拉向月球，从而在海岸线上产生高潮。在地球的另一侧（即对跖点）也会感受到同样高的潮汐。当月球不在地球的地心或对跖点时，就会观察到低潮。由于液体水比构成固体地球的岩石更容易受到月球引力的影响，你可能对海洋潮汐更加熟悉，但也有地球潮汐，它会导致地球随着月球的运动而膨胀。太阳也会对地球施加一些引力，并根据季节改变潮汐的大小。你现在可以解释一天的长度，一个朔望月的长度，潮汐，但是什么导致了一年的长度。

地球绕太阳运行，一年。

整个地球不仅在自转，而且还在太空中沿着围绕太阳运行的轨道运行。与月球不同，地球的极轴相对于太阳倾斜了23.5°，因此在这段绕太阳运行的旅程中，有一半时间北极朝向太阳，南极背向太阳。地球自转倾斜23.5°导致北半球在更靠近太阳时（6月、7月、8月）白天更长，南半球白天更短，而北半球白天更短（11月、12月、1月）与南半球白天更长相对应。由于地球轴线的倾斜，我们有了春、夏、秋、冬四个季节，每个半球的季节都有所不同。

你可能会惊讶地发现，地球绕太阳运行的轨道不是一个完美的圆形，正如太阳系图示中经常描绘的那样，而是以椭圆轨道绕太阳运行。在地球上，可以通过记录一年中每天中午太阳的位置来证明这一点，这将描绘出一个8字形，在天空中被称为天体周年视运动图。在8字形顶部的太阳中午位置将发生在夏至日，而8字形底部的太阳中午位置将发生在冬至日，天空中的两个点之间的距离代表地球的倾斜角23.5°。然而，8字形的宽度是由于地球绕太阳运行的椭圆路径造成的。8字形不是一个完美的8字形，而是其中一个环比另一个大。

这是由于太阳并不直接位于地球绕其运行的椭圆轨道的中心。在 12 月至 1 月期间，地球离太阳更近，而在 6 月至 7 月期间，地球离太阳更远。地球最靠近太阳的年份被称为近日点，而地球最远离太阳的年份被称为远日点。

这与你想象的相反，因为在北半球，你在寒冷的冬季月份离太阳更近，而在炎热的夏季月份，你离太阳更远。

到太阳的距离从 0.9833 个天文单位到 1.0167 个天文单位不等，其中天文单位是天文单位，定义为地球到太阳的平均距离，即 1.5 亿公里（9300 万英里）。因此，地球到太阳的距离每年大约相差 500 万公里（310 万英里）。

虽然地球绕太阳运行的轨道似乎是一堆需要记忆的数字和事实，但发现太阳而不是地球是太阳系的中心是一个重大的科学发现。这种思维革命的原因是，几个世纪以来，人们提出了一个同样有效的解释，来说明地球轨道的年度循环。

托勒密错误的太阳系地心模型

在法老克利奥帕特拉去世和埃及亚历山大城被罗马吞并后不久，一位名叫克劳狄乌斯·托勒密的天文学家住在亚历山大城。托勒密的热情是绘制星空，他注意到，每天晚上火星的运行路径相对于夜空中其他恒星的运行路径会有所不同。在公元 58 年左右的几年时间里，他记录了火星在夜空中的运行路径，证明了火星在几个月的过程中在夜空中循环。例如，火星会在几个星期内与恒星一起移动，但随后会循环回来几个星期，然后在继续向它开始的方向移动之前，再次循环回来。

火星相对于背景恒星在几个月内的明显运行路径，显示了它相对于地球的轨道“逆行环”。

由于火星的运行路径循环回来，托勒密认为这种运动是逆行运动，而当火星与恒星一起正常运行时，则是顺行运动。托勒密遵循亚里士多德的希腊传统，即地球是宇宙的中心。那么为什么火星和金星会在地球上循环呢？它们应该在夜空中沿着直线运行，因为它们绕地球运行，而不是绕太阳运行？他设计了一个复杂的太阳系地心模型，表明火星的轨道以及其他已知的行星（如金星）遵循本轮，即在它们绕地球运行的轨道之外的另一个圆形轨道。人们花了一千五百年才推翻托勒密的太阳系模型。

哥白尼正确的太阳系日心模型

尼古拉·哥白尼在 1543 年出版的《天体运行论》一书中发表了他的另一种观点。太阳系日心说将太阳置于太阳系的中心，而不是地球。在这样做的时候，哥白尼证明了本轮轨道实际上是由于从地球上观察到火星在它自己绕太阳运行的轨道上运行而造成的。

由于地球离太阳比火星更近，因此看起来火星在夜空中的运行路径有一个环，而实际上两颗行星都在绕太阳运行，但地球的轨道比火星更靠近。

哥白尼认为，太阳系就像行星在圆形跑道上比赛一样。地球在内圈，而火星在外圈。当地球沿着内圈的轨道运行时，对火星的外圈轨道的观察会发生变化。逆行运动自然而然地作为从移动的地球视角观察移动的火星的结果而产生。哥白尼拒绝了产生逆行运动所需的本轮，而行星绕太阳运行的轨道是圆形的。哥白尼的书是有史以来出版的最重要的科学书籍之一，但仍然需要一些修改，例如，地球绕太阳运行的轨道是椭圆形的，而不是圆形的，其他行星也是如此。

你在太空中以多快的速度飞行？

在本模块的开头，我们讨论了你在太空中以多快的速度飞行，并使用了地球的自转或旋转，现在我们可以添加地球绕太阳运行的轨道成分。地球绕太阳运行的距离是 9.4 亿公里（5.84 亿英里），它每 365.256 天完成一次。一年不能被天数平均分配，因此日历必须每 4 年添加一天，或者说是“闰日”。我们可以确定这种绕太阳运行的运动速度，并确定地球及其表面的一切事物以每小时 66,619.94 英里或每小时 107,230.73 公里的惊人速度绕太阳运行。想象一下，当你坐在那里阅读本文时，你正以这种难以置信的速度坐在一颗围绕恒星运行的行星上，速度是世界上最快飞机速度的 30 倍。因为你确实在这样做！

这一惊人的事实，即你正乘坐一个快速移动的物体在太空中高速行驶，启发了理查德·巴克敏斯特·富勒在 1969 年创造了地球只是一艘在浩瀚宇宙中航行的飞船的概念。地球号飞船，正如他称我们的星球一样，只是一艘巨大的船，就像一艘在空旷的宇宙海洋中航行的战舰。他警告说，你和这艘“宇宙飞船”上的所有生命都应该为漫长的航行做好准备。

地球的银河系之旅

约翰·米歇尔，来自英国约克郡的矮胖牧师，他设计了证明地球不是空心的实验，他在 1784 年写的一封信中提出，宇宙中可能存在一些物体，它们的质量如此之大，以至于它们的引力加速度甚至会吸收光线，他称这些神秘的超大质量天体为“暗星”。如今，我们称它们为黑洞。寻找宇宙中这些神秘超大质量天体的努力因他的建议而得到加强，即这些天体的引力效应可能在附近的可见天体中看到。然而，它们仍然是仅仅从牛顿方程式推导出具有巨大质量（比太阳大数百万倍）的天体的数学好奇现象。

1950 年，宇宙中还没有人观测到这些超大质量天体之一，而Jocelyn Bell，一个在英国寄宿学校的年轻女孩，正在为以烹饪和缝纫为主的女子课程而苦恼。当一个科学课程开设时，只有男孩被允许参加。她和她父母愤怒地抗议，最终她被允许和其他两名女生一起参加科学课。Jocelyn Bell最喜欢物理学，1965 年她继续在剑桥大学学习物理学。她加入了一个研究团队，监听来自外太空的无线电波。他们一直在接收来自微弱恒星的无线电波脉冲和杂音。科学家称这些信号为类星体无线电源，美国天文学家丘宏义简称为类星体。1967 年夏天，Jocelyn Bell 和她的教授安东尼·休伊什正在查看新建造的射电望远镜阵列的打印输出，这些阵列旨在探测来自太空的类星体信号。她注意到每 1.3373 秒出现一个规律的脉冲模式，虽然很想将这些无线电波模式归因于外星人，但他们开玩笑地称这些规律的脉冲信号为“小绿人”，但他们意识到，和其他科学家一样，这个无线电信号是由一个具有巨大引力的超大质量天体产生的。通过望远镜观察，信号来自一颗微弱的恒星，被认定为中子星，一颗极其巨大的恒星，以难以置信的速度旋转，每 1.3373 秒发射一次电磁辐射脉冲。这些无线电信号被认为是在星云状气体被拉入这些超大质量恒星形成吸积盘时产生的，当这些气体穿过吸积盘落入中子星时，会发出强大的磁场和无线电波——就像巨大的闪电。

科学家意识到，可以使用大型射电望远镜阵列来绘制这些来自太空的信号到天空上，从而探测到这些超大质量天体。

研究人员将注意力集中在夜空中最亮恒星之一的中心，它实际上是一个名为M87的星团，也称为室女座 A，是室女座中最亮的一点。它在 1781 年被梅西耶认定为一个星团，并被哈勃在 1931 年归类为一个椭圆星云。今天它被称为一个包含数十亿颗恒星的星系。

来自M87的无线电波表明，在其中心附近存在一个超大质量天体，代表一个黑洞。2019 年，事件视界望远镜，一个射电望远镜网络，将目光集中在这个点，并对来自其中心的信号成像，产生了第一个黑洞图像，它看起来像一个幽灵般的黑暗斑点，周围环绕着光。黑暗斑点的中心是一个质量是太阳 65 亿倍、距离地球 5500 万光年的天体。

事件视界望远镜还将目光集中在夜空中一个由无线电波于 1974 年首次探测到的点，该点被认为是我们自己的银河系的中心，即银河系。在夜空中，一串星星似乎在特别黑暗的夜晚扫过天空。这些恒星是你在你自己的星系中存在的最近的恒星邻居。银河系是一个包含数十亿颗恒星的集合，包括围绕一个中心点旋转的太阳。银河系的中心位于靠近人马座 A* （发音为“人马座 A 星”）的恒星附近，位于人马座。在这里，已经观察到附近的恒星围绕一个点旋转，该点是另一个黑洞的位置，该黑洞的质量是太阳的 400 万倍，距离地球只有 25,000 光年。它是距离你最近的超大质量黑洞。

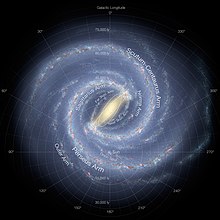
天文学家已经测量了太阳绕银河系中心这个点的旋转速度，并确定整个太阳系大约需要 2.4 亿到 2.3 亿年才能完成围绕这个黑洞的银河轨道运行。上一次我们太阳系占据这个相对于人马座 A*的空间，是在恐龙在地球上进化之前！

然而，不要认为太阳系围绕这个点的运行速度很慢。地球和整个太阳系正以令人难以置信的速度沿着这条路径前进。

鉴于 1 光年等于 5.879 x 1012 英里，并且绕行 1.5708 亿光年的周长，或者说在 2.1024 x 1012 小时内绕行 9.23471 x 1017 英里的路径需要 2.4 亿年，我们的太阳系正在以每小时 439,246 英里的速度围绕这个黑洞高速运行！

你确实身处一艘非常快的宇宙飞船，地球相对于其极轴的运动速度在每小时 0 到 1,040.45 英里（每小时 1674.44 公里）之间，具体取决于你的纬度。地球相对于太阳的运动速度为每小时 66,620 英里（每小时 107,214.5 公里），地球相对于人马座 A*的银河系运动速度为每小时 439,246 英里（每小时 706,898 公里）。

图书页面导航
上一页	当前页	下一页
d. 如何使用指南针、六分仪和计时器在全球范围内导航。	e. 地球的运动和自转。	f. 时间的本质：太阳历、阴历和恒星历。