等离子体聚变前言

本书旨在描述一些关于聚变能及其产生的基本考虑因素。然而，其重点不仅仅在于聚变能本身，还在于理解相关的物理现象，例如压力。

自然界中的等离子体

萨哈方程指出

${\frac {n_{i}}{n_{n}}}=2.4*10^{21}{\frac {T^{3/2}}{n_{i}}}\exp -({\frac {U_{i}}{kT}})$,

其中 n_i 是离子密度，n_n 是中性原子密度，U_i 是气体的电离能。

对于普通空气而言

$n_{n}=3*10^{25}m^{-3}$

$T=300K$

$U_{i}=14,5eV(nitrogen)$

得出

${\frac {n_{i}}{n_{n}}}=10^{-122}$

这是一个极低的数值

当 U_i 仅为 kT 的几倍时，电离率才会保持较低水平。

因此，在地球上不存在自然等离子体，只存在于温度高达数百万度的天体中。

数值示例

根据下面的公式（如果正确的话），太阳内部的压力似乎在250万个大气压的量级，而其（表面）温度约为50000K。我们可以使用公式 p=nkT 计算粒子密度 (n)，使用这个公式，我计算出的 n 为 3,6E29（比空气密度高约10000倍）。在这里，我们可以使用萨哈方程计算氢离子 (n_i) 与中性氢原子 (n_n) 的比例 (n_i/n_n)，同时使用氢的电离能 (Ui=13,6eV)，得出比例为5,6%。

关于太阳压力的未经证实的观点

来自某全方向物体的光强 (I) 为

$I={\frac {P}{4\pi R^{2}}}$

其中 P 是辐射功率，R 是距离，这可能会导致

$\rho =\rho _{0}(1-{\frac {4\pi R^{2}}{4\pi b^{2}}})=\rho _{0}(1-{\frac {R^{2}}{b^{2}}})$

然后质量 (m) 为

$M=\int \rho dv=\int _{0}^{b}\rho 4\pi R^{2}dR$

其中 b 是太阳的半径，R 是太阳中某个半径，这给出

$M=4\pi \rho _{0}[{\frac {R^{3}}{3}}-{\frac {R^{5}}{5b^{2}}}]=4\pi \rho _{0}R^{3}[{\frac {1}{3}}-{\frac {R^{2}}{5b^{2}}}]$

然后压力为

$p=\rho gh=\rho gR=\rho {\frac {GM}{R^{2}}}R=\rho {\frac {GM}{R}}$

因此

$p=\rho _{0}(1-{\frac {R^{2}}{b^{2}}})G4\pi \rho _{0}R^{2}({\frac {1}{3}}-{\frac {R^{2}}{5b^{2}}})$

平均密度为

${\tilde {\rho }}={\frac {M}{V}}$

和

$\rho =\rho _{0}(1-{\frac {R^{2}}{b^{2}}})$

因此

${\tilde {\rho }}={\frac {1}{b}}\int _{0}^{b}\rho _{0}(1-{\frac {R^{2}}{b^{2}}})dR$

这给出

${\tilde {\rho }}=2/3\rho _{0}$

结果是

$\rho _{0}={\frac {3}{2}}{\tilde {\rho }}={\frac {3M}{2V}}$

然后压力为

$p=({\frac {3M}{2V}})^{2}(1-{\frac {R^{2}}{b^{2}}})G4\pi \rho _{0}R^{2}({\frac {1}{3}}-{\frac {R^{2}}{5b^{2}}})$

现在我们需要检查 R 应该取什么值，我在下面计算得出该函数有一个极小值/极大值（取决于你所处的方向），这个点可以通过常规求导并令导数为零来找到，对 R 求导该公式得到：

${\frac {2}{3}}-{\frac {32}{15}}({\frac {R}{b}})^{2}+{\frac {6}{5}}({\frac {R}{b}})^{4}=0$

我们通过代入进行变量替换：

$x=({\frac {R}{b}})^{2}$

这给出

$x^{2}-{\frac {160}{90}}x+{\frac {10}{18}}=0$

求解这个二阶方程得到：

$x={\frac {16}{18}}-{\sqrt {({\frac {16}{18}})^{2}-{\frac {10}{18}}}}$

其中，只有根式前为减号的解是可能的，因为否则 R>b，数值解为：

$x=0,89-0,48=0,40$

因此

${\frac {R}{b}}=0,63\approx {\frac {2}{\pi }}$

我认出了这个值是全波整流信号的直流值，那么 b(太阳) 为 700Mm，这表明在 446Mm 半径处存在一个极大值/极小值，物理手册中指出：

$M(Sun)=333000m(Earth)$

和

$V(Sun)={\frac {4\pi b_{s}^{3}}{3}}=1,4\cdot 10^{27}$

不幸的是，物理手册中没有给出地球的质量，但我天真地尝试通过将地球视为主要由水组成来估计它，b(地球)=6370km，我得到：

$m(Earth)\approx \rho _{H_{2}O}\cdot {\frac {4\pi b_{j}^{3}}{3}}=10^{24}$

由于这个估计，我得到：

$M=3,3\cdot 10^{29}$

这使得太阳的平均密度为：

${\tilde {\rho }}={\frac {M}{V}}=238kg/m^{3}$

我认为这相当低，但我们应该记住它是一种气体/等离子体，而空气的密度要低 200 多倍，重力常数则为

$G=6,62\cdot 10^{-}{11}$

有了这个值，我们现在可以计算太阳的压力，结果是

$p=7\cdot 10^{9}Pa=70000atm=70ton/cm^{2}$

这是一个相当大的压力，请记住，正常的空气压力就像用 1 公斤的力在一个桌子上戳一下手指，可以通过使用斯特藩-玻耳兹曼辐射定律来估算太阳的温度，该定律指出强度与 T^4 成正比，这得出

${\frac {T_{s}^{4}}{4\pi (AU)^{2}}}={\frac {T_{j}^{4}}{4\pi R_{j}^{2}}}$

其中 AU 是天文单位，即太阳到地球的距离，Rj 是地球的半径，使用这个公式，我们得到

$T_{s}=({\frac {AU}{R_{j}}})^{\frac {1}{2}}T_{j}$

其中 Tj=300K，Rj=6370km 以及 AU=1,5E11 得出

$T_{s}=46000K\approx 50000K$

现在我们有了太阳的压力和温度，就可以计算出粒子的密度，如下

$p=nkT$

这得出粒子的离子密度 (n_i) 为

$n_{i}=10^{28}$

这应该与普通空气中的粒子密度进行比较，普通空气的粒子密度约为 E25，因此太阳中的粒子密度似乎高出 1000 倍，然而我的计算结果表明，密度在向中心方向增加 50%，我顺便说一下，使用了表面温度，而表面温度很可能在太阳的核心更高，如果我的公式是正确的，很明显太阳核心的压力可能比上述结果高出 7 倍（只需将 R=0 代入），使用上述萨哈方程和氢的电离能 13,6eV，我们现在可以计算出太阳中的离子比例为 11%。

我现在已经通过在维基百科中查找信息来修正了我对地球质量的估计，看来地球的质量高出 6 倍，这实际上使我的压力估计高出 36 倍，因此太阳中的压力应该是 2 500 000atm=2 500 000kg/cm^2！

基本考虑

当带电粒子在磁场中运动时，以下方程适用

$m{\frac {dv}{dt}}=qvXB$

解决该方程的一个简单方法是设置

$v=v_{0}e^{jwt}$

然后该方程变为

$mjwv_{0}e^{jwt}=qvXB=mjwv$

仅考虑大小，我们得到

$w_{c}={\frac {|q|B}{m}}$

而当 v=wr 时，我们得到

$r_{L}={\frac {mv}{|q|B}}$

其中 w_c 称为回旋频率，r_L 称为拉莫半径。

这意味着粒子将以回旋频率和拉莫半径绕力线旋转。

这是等离子体能够被磁场约束的最基本原因。

数值示例

如果我们看一下电子和大约 5T 的磁通密度（我认为 ITER 使用的磁通密度，但信息不幸地在维基百科时代被删除了），我们得到的回旋频率为 8E11 rad/s。我还记得 ITER 的热能约为 10keV，使用下面的能量公式可以算出电子的速度约为 5,6E7 m/s，得到的拉莫半径约为 70um。如果我们看一下质子（以相反的方向旋转），回旋频率变为 4,8E8 rad/s，在相同的温度下得到的速度为 1,4E6 m/s，得到的拉莫半径为 2,9mm。也就是说，拉莫半径大约分别为 0,1mm 和 1mm。

等离子体的能量和温度

平均能量可以写成

$E_{AV}={\frac {1}{2}}mv^{2}\approx kT$

对于每一个自由度，都有一个额外的 kT/2 （无论它意味着什么），速度为

$v={\sqrt {\frac {2kT}{m}}}$

上面的能量方程符合麦克斯韦速度分布函数

$f(v)=A\exp {(-{\frac {mv^{2}/2}{kT}})}$

其中常数 A 可以通过以下公式计算

$1=\int _{-\infty }^{\infty }f(v)dv$

这使我们得到

$A={\sqrt {\frac {m}{2\pi kT}}}$

这意味着

$<kT>={\frac {mv^{2}}{2}}$

其中 <kT> 是平均值，换句话说，有些粒子的“温度”高于平均动能。

数值示例

分布函数的指数部分在速度为 0 m/s 时最大，但曲线下的面积代表所有速度都被考虑在内的概率 1，这意味着必须将分布函数对所有速度进行积分，从而通过将积分设置为 1 来确定常数 A。300K 时电子上的 A 为 6,2E-6。

eV 和一些常数

根据弗朗西斯·F·陈的说法，物理学家使用 eV 来避免混淆，但 kT 是用焦耳表示的，因此需要使用以下公式进行转换：

$kT/q=eV$

电位是用伏特表示的，但它们的能量 (qU) 可以像原样一样被认为是用 eV 表示的。

让我们列出一些常数

$k=1,38\cdot 10^{-23}J/K$

$q=1,6\cdot 10^{-19}As$

$m_{p}=1,67.2623\cdot 10^{-27}kg$

$m_{n}=1,67.4929\cdot 10^{-27}kg$

$m_{e}=9,10.9390\cdot 10^{-31}kg$

$h=6,63\cdot 10^{-34}Js$

$\mu _{0}=4\pi \cdot 10^{-7}Vs/Am$

$\epsilon _{0}=8,85\cdot 10^{-12}As/Vm$

推导出电流环的磁通密度

电流环产生的磁场

从麦克斯韦方程组中我们可以得到

$\nabla \cdot B=0$

它可以被重写为

$B=\nabla XA$

其中A可以是一个任意向量。

使用向量磁势

$A={\frac {\mu _{0}}{4\pi }}\int _{v}{{\frac {J}{R}}dv}$

并意识到

$Jdv=JSdl=Idl$

我们根据毕奥-萨伐尔定律得到

$B={\frac {\mu _{0}I}{4\pi }}\oint _{c}{\frac {dlXa_{R}}{R^{2}}}$

定义

$dl=bd\phi a_{\phi }$

和

$R=a_{z}z-a_{r}b$

和

$dlXR=a_{\phi }bd\phi X(a_{z}z-a_{r}b)=a_{r}bzd\phi +a_{z}b^{2}d\phi$

并意识到r部分相互抵消，我们得到

$B={\frac {\mu _{0}I}{4\pi }}\int _{0}^{2\pi }a_{z}{\frac {b^{2}d\phi }{(z^{2}+b^{2})^{3/2}}}$

或者

$B={\frac {\mu _{0}I}{2}}{\frac {b^{2}}{(z^{2}+b^{2})^{3/2}}}={\frac {\mu _{0}I}{2}}{\frac {b^{2}}{R^{3}}}{\hat {z}}$

其中B的维度很明显是

$B\propto {\frac {1}{R}}$

数值示例

如果 b=2m 且 I=100A，距离 (R) 为 1m 处的磁通密度 (B) 仅为 0,25mT，与某些 5T 的主要力线相比，这并不多，因此可以说，回旋电流不影响 B 场。

推导带电环路的电场强度

带电环路的 E 场

可以这样写 E 场

$E={\frac {\rho _{L}}{4\pi \epsilon _{0}}}\int {\frac {dl'}{R^{2}}}={\frac {\rho _{L}}{4\pi \epsilon _{0}}}\int {\frac {dl'R}{R^{3}}}$

其中分母中的 R 是一个向量，像

$R=-b{\hat {r}}+z{\hat {z}}$

和

$dl'=bd\phi$

由于对称性，不存在 r 分量，这给了我们

$R=z{\hat {z}}$

它可以被重写为

$E={\frac {\rho _{L}}{4\pi \epsilon _{0}}}\int {\frac {bd\phi }{z^{2}}}{\hat {z}}$

或者

$E={\frac {\rho _{L}}{4\pi \epsilon _{0}}}\int {\frac {bd\phi }{R^{2}}}{\hat {z}}$

最后

$E={\frac {\rho _{L}}{4\pi \epsilon _{0}R^{2}}}2\pi b{\hat {z}}$

实际上它表示 Q/R^2，它与 E 有相同的“维度”，然后你可以观察到对于正电荷，E 位于 z 方向，rho_L 可以被看作（并且不一定是均匀的）

$\rho _{L}={\frac {\sum q}{2\pi b}}$

或者

$\rho _{L}={\frac {\sum q}{2\pi r_{L}}}$

其中 E 的维度很明显是

$E\propto {\frac {1}{R^{2}}}$

数值示例

如果质子的拉莫半径 (b) 为 2.9 毫米，则其圆周可以容纳 1.4E22 个质子，总电荷量为 0.22 微库仑，这反过来又产生 12.7 微库仑/米的线电荷密度 (rho_L)。在距离 (R) 为 1 米处，我们得到 2.2 千伏/米的电场强度 (E)，这并不算低（空气的介电强度约为 5 兆伏/米），但这种情况永远不会发生，因为粒子会不断相互碰撞。

关于电流/带电环路的未经证实的观点

我手动恢复了关于电流环路产生的磁通密度 (B) 的章节，因为我认为它比我想象的要深刻得多。当然，电流在环路中旋转，我们从中得到了一个 Bz 场，但是电流是运动中的电荷。我推测例如质子具有相同的拉莫半径，这意味着质子没有必要彼此并排围绕力线旋转，它们也可以像一串珍珠一样互相追随旋转，本质上可以将其视为被质子塞满的“珍珠项链”，质子的运动产生电流，进而产生 B 场。

我的想法是，质量和电荷相同的粒子以相同的回旋频率和拉莫半径沿着力线旋转。如果我们可以认为相同电荷的粒子实际上是“互相追随”旋转的，我们有两种情况。

1) 由旋转粒子围绕局部 Bz 场产生的电流（即来自电流的 B_phi，该电流的方向为 z 方向）会产生一个 B_phi 场，就我理解而言，如果电荷为正（并且在局部 phi 方向运动），这会放大现有的 B_phi 场。

2) 当我们有一串粒子围绕旋转时，我们也会有一个静态 E 场的“快照”。E 场似乎也会放大局部 phi 方向的现有 E 场。

带正电的粒子显然具有正的 Ez 分量，我不确定，但根据洛伦兹力方程

$q(vXB)=m{\frac {dv}{dt}}$

并使用

$v_{r}=v_{0r}e^{jwt}$

和

$v_{\phi }=v_{0\phi }e^{jwt}$

并为了简单起见认识到

$v=(0;v_{\phi };0)$

和

$B=(0;0;B_{z})$

运动必须是

$qv_{0\phi }e^{jwt}B_{z}=jwmv_{0r}e^{jwt}$

其中

$e^{jwt}$

可以简化，我们剩下

$qv_{0\phi }B_{z}=jwmv_{0r}$

其中 0 仅表示幅度。去掉零，我们得到

$qv_{\phi }B_{z}=jwmv_{r}$

有了这些（新的）方向，实际上意味着回旋频率公式

$w_{c}={\frac {qB}{m}}$

是错误的，应该是

$w_{c}={\frac {1}{j}}{\frac {qB_{z}}{m}}{\frac {v_{\phi }}{v_{r}}}={\frac {qB_{z}}{m}}{\frac {v_{\phi }}{v_{r}}}\angle {-90\deg }$

这意味着为了使 w_c 存在，必须存在 v_r 漂移，这意味着拉莫尔半径会随着时间推移而增加，因此不稳定，牢固的 B 不会使粒子始终以相同的半径绕力线旋转（我在这里可能错了）。

最后看起来像

$0=qE+q(vXB)$

我描述的这些环路实际上意味着 E 和 B 以类似的方式增加，E 和 B 相乘的常数显然无关紧要，因为它可以被短路，那么方程是稳定的，不考虑 E 和 B 可能不会以相同的方式增加。

等离子体中的漂移

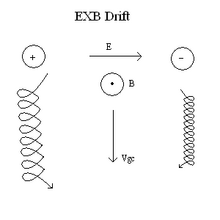这张图片展示了 E 场如何与 B 场相互作用以改变粒子轨道。

这张图片描述了磁场不均匀时粒子会发生什么。

该图描述了等离子体中的离心漂移。

使用

$m{\frac {dv}{dt}}=q(E+vXB)$

并将它设为零，因为我们正在检查等离子体是否可以自行静止，这给了我们

$0=q(E+vXB)$

可以改写为

$E=-vXB$

如果我们然后从右边对 B 进行叉积，我们得到

$EXB=BX(vXB)$

然后我们可以使用“BAC-CAB”规则，这意味着

$AXBXC=B(A\cdot C)-C(A\cdot B)$

对此的证据相当复杂，所以我不会在这里证明它，但是

$EXB=BX(vXB)=vB^{2}-B(B\cdot v)$

该方程的横向分量是

$v_{gc}={\frac {EXB}{B^{2}}}$

这个引导中心漂移的大小是

$v_{gc}={\frac {E}{B}}$

意识到

$F=qE$

可以设置

$v_{force}={\frac {1}{q}}{\frac {FXB}{B^{2}}}$

其中 F 可能是

$F_{E}=qE$

由于 E 场或

$F_{g}=mg$

由于重力或

$F_{cf}=a_{r}{\frac {mv_{//}^{2}}{R_{c}}}$

由于粒子沿着力线运动时的离心力，那么 E 引起的漂移将是

$v_{E}={\frac {EXB}{B^{2}}}$

而重力引起的漂移将是

$v_{g}={\frac {m}{q}}{\frac {gXB}{B^{2}}}$

而弯曲的B场引起的漂移将是

$v_{R}={\frac {1}{q}}{\frac {F_{cf}XB}{B^{2}}}={\frac {mv_{//}^{2}}{qB^{2}}}{\frac {R_{c}XB}{R_{c}^{2}}}$

值得注意的是

$|v_{E}|=|{\frac {E}{B}}|$

在非均匀B场中，力的表达式可以写成

$F=-/+{\frac {qv_{\perp }r_{L}}{2}}{\frac {dB}{dy}}{\hat {z}}$

其中v_$\perp$表示垂直于B_phi的速度，将其代入上述力公式，得到导向中心漂移

$v_{gc}={\frac {1}{q}}{\frac {F_{z}XB_{\phi }}{B^{2}}}={\frac {1}{q}}{\frac {F_{z}X{\hat {B}}_{\phi }}{B}}=-{\frac {1}{q}}{\frac {|F|}{|B|}}{\hat {r}}=-/+{\frac {v_{\perp }r_{L}}{2B}}{\frac {dB}{dr}}{\hat {r}}$

其中索引仅显示重要分量，它们仍然是向量，叉积表示F_z由于B仅在phi方向产生一个r分量，但是B_phi根据1/r衰减，因此这里存在B梯度，上面可以推广为

$v_{\nabla B}=-/+{\frac {v_{\perp }r_{L}}{2}}{\frac {\nabla BXB}{B^{2}}}$

即grad-B漂移或由B的不均匀性引起的漂移，因此可以证明弯曲真空场中的总漂移为

$v_{cv}=v_{R}+v_{\nabla B}={\frac {m}{qB^{2}}}{\frac {RcXB}{Rc^{2}}}(v_{//}^{2}+{\frac {1}{2}}v_{\perp }^{2})$

"不幸的是，这些漂移会叠加。这意味着如果将磁场弯成环面以用于约束热核等离子体，那么无论如何调整温度和磁场，粒子都会从环面中漂移出来"-- Francis F. Chen

数值示例

如果我们观察重力漂移 (v_g) 并运行 5T 的 ITER B，我们会发现对于电子，v_g 为 1.2E-11 m/s，对于质子，v_g 为 2E-8 m/s。这些速度并不高，但随着时间的推移，粒子会从等离子体中漂移出去，无论我们如何调整磁通密度 (B)，但我对如此低的速率感到惊讶。另一方面，我们还需要考虑其他类型的漂移，这是最容易计算的。

等离子体作为流体

如果我们将等离子体视为流体，我们有

$mn[{\frac {dv}{dt}}+(v\cdot \nabla )v]=qn(E+vXB)-\nabla p$

其中可以证明左边两项可以忽略。

如果我们然后取与 B 的叉积，我们有

$0=qn[EXB+(v_{p}XB)XB]-\nabla pXB$

或者

$0=qn[EXB-v_{p}B^{2}]-\nabla pXB$

其中一项是故意省略的。

重新排列以上公式得到等离子体作为流体的总垂直漂移

$v_{p}={\frac {EXB}{B^{2}}}-{\frac {\nabla pXB}{qnB^{2}}}=v_{E}+v_{D}$

其中所谓的反磁漂移是

$v_{D}=-{\frac {\nabla pXB}{qnB^{2}}}$

其中力是

$F_{D}=-{\frac {\nabla p}{n}}$

意味着压力的梯度

$p=nkT$

与体积粒子密度成正比。

对于等温等离子体，我们有

$\nabla p=kT\nabla n$

数值示例

在 300K 和普通空气中氮气密度约为 E25 时，压力变为 41kPa，这与约为 1E5Pa 的正常大气压不同，这让我觉得密度可能略高，2.5E25 则使其变得正确。

标准模型

1. 电子和正电子（“反电子”）
2. μ 子和反μ 子
3. τ 子和反τ 子

除此之外，还有它们的相应中微子和反中微子，总共六种不同的粒子类型，即

1. 电子
2. 电子中微子
3. μ 子
4. μ 子中微子
5. τ 子
6. τ 子中微子

中微子是无质量的，因此很难探测。

其中最主要的三个是基本粒子，由夸克组成。就我们而言，识别两种类型的夸克就足够了，即上夸克和下夸克。这是因为中子由两个下夸克和一个上夸克组成，而质子由两个上夸克和一个下夸克组成。

正如 PF 的导师所解释的那样，中子可以经历弱相互作用（嬗变）并转化为质子，释放出一个电子和一个反中微子。这与夸克可以改变其类型/味道有关。在这种情况下，一个下夸克只需要改变为一个上夸克就可以使粒子发生改变。

也有人解释了质子如何以类似的方式转化为中子。

这是我们太阳诞生时所有质子可以生成中子，从而产生氘，从而真正开始聚变过程产生氦的原因。

如果我被允许思考任何东西，我认为这些理论仅仅是花哨的粒子。

数值示例

根据物理手册，μ 子的质量为 106MeV/c^2，τ 子的质量为 1807MeV/c^2。1Mev 的能量在焦耳中表示为 1.6E-13J，这使得μ 子的质量为 1.7E-11J/c^2，τ 子的质量为 2.9E-19J/c^2，分别得到它们的质量为 1.9E-30kg 和 3.2E-29kg。我所知道的最小粒子是电子，其质量约为 1E-30，因此μ 子的质量约为两个电子质量，τ 子的质量约为 32 个电子质量。

辐射粒子

1) β 粒子（电子）

2) α 粒子（普通氦 4 核）

3) γ 射线（从原子核发射的高能光子）

4) X 射线（电子减速或加速时发射的能量略低的光子）

数值示例

γ 射线开始时的能量为 10keV，这意味着波长为 1Å，普通可见光的波长在 10Å 和 100Å 之间。

玻尔模型推导

已经证明

$n\lambda =2\pi r$

这意味着电子轨道的长度必须是波长的整数倍。

使用德布罗意波长

$\lambda =h/p$

和

$\hbar =h/2\pi$

上述等式可以改写为

$pr=mvr=n\hbar$

参考基本力关系，其中向心力等于电磁力，我们可以写成

${\frac {mv^{2}}{r}}={\frac {ke^{2}}{r^{2}}}$

其中

$k={\frac {1}{4\pi \epsilon _{0}}}$

求解 v 得到

$v={\sqrt {\frac {ke^{2}}{mr}}}$

对电磁力积分得到势能为

$E_{p}=-{\frac {ke^{2}}{r}}$

动能通常可以写成

$E_{k}={\frac {mv^{2}}{2}}$

使用上述 v 的表达式将 Ep 与 Ek 相加得到

$E_{tot}=E_{p}/2=-{\frac {ke^{2}}{2r}}$

现在，

$mrv=mr{\sqrt {\frac {ke^{2}}{mr}}}={\sqrt {ke^{2}mr}}==n\hbar$

求解 r 得到

$r={\frac {n^{2}\hbar ^{2}}{ke^{2}m}}$

对于 n=1，这被称为玻尔半径，对于氢，可以证明它大约是 0,5Å。

使用这个方程和上述速度表达式得到

$v={\frac {ke^{2}}{n\hbar }}$

这表明速度如何离散地取决于壳层数 (n)。

对于可选原子，你可以将 k 视为 kA，其中 A 是原子序数（但这在现实生活中并不准确）。

数值示例

如果从 n=1 跳到 n=2，能量差将以 hf=10,2eV 的光子辐射，这意味着波长为 0,122Å。

质子-质子聚变

这些陈述引用自

1）质子聚变

2）一个质子转化为一个中子形成氘（释放一个正电子和一个电子中微子），这使得

$H_{1}^{2}$

3）氘与另一个质子聚变（也释放伽马射线），这使得

$He_{2}^{3}$

4) 两个产生的氦-3 核聚变，得到

$2xHe_{2}^{3}=He_{2}^{4}+2p$

5) 一个阿尔法粒子 (氦-4) 形成，并释放两个质子，完成整个过程。

亚瑟·爱丁顿的一句名言

"我知道许多批评家认为恒星不够热。这些批评家把自己暴露在明显的反驳之下；我们告诉他们去寻找一个更热的地方。"

数值示例

如果能量增益可以写成 Eb(after)-Eb(before) ，那么当 He3 产生时，Eb(He3)-Eb(H)=7,8-2,2=5,5MeV 的能量增益。

关于质子-质子聚变的未经证实的观点

我认为质子-质子聚变应该写成

$p+p+e+e->p+n^{-}+\Delta E_{b}$

这里我们有质量守恒，因为 n>~p+2e ，但我们有一个带负电荷的中子，这么说吧，我们可以把它改写成

$H_{1}^{1}+H_{1}^{1}=H_{1}^{2-}+\Delta E_{b}$

但是根据定义，在 (高温) 等离子体中不存在中性原子。

理论上，两个质子可以聚变为

$He_{2}^{2}$

但这种同位素不存在 (根据物理手册)，最简单的氦同位素是

$He_{2}^{3}$

它再次使用了一个中子。我认为中子是某种核心的粘合剂，但是还有更科学的理论，叫做汤川力 (或势能) ，但它听起来像是方便的杜撰。

另一方面，质子的万有引力与库仑斥力的比率大约为

$10^{-36}$

因此万有引力对将一对质子束缚在一起没有多大用处，但也许秘密在于中子？

所有物质都有同位素，但它们很少能摆脱几个中子来保持稳定。

物理手册指出

$p=1,67.2623\cdot 10^{-27}kg$

$n=1,67.4929\cdot 10^{-27}kg$

$e=9,10.9390\cdot 10^{-31}kg$

这给出

$n-p-e=1,53m_{e}$

这是从质子和电子产生中子的最简单过程，这里我们至少有了中性电荷，但质量相差 1,53m_e。

我们或许可以将这个过程写成

$n-p-e=1,53m_{e}c^{2}$

或者

$n-p-e=780keV$

根据爱因斯坦的理论。

现在，如果能量和质量可以相互转换，我们如何在还没有开始的過程中获取 780keV 的能量呢？

热能与粒子速度密切相关，那么我们如何将这种“速度”转换为质量呢？

我认为这是不可能的，上面的爱因斯坦关系只是理论上的。换句话说，我们是否被困于这样一个事实，即该过程的质量差为 1.53m_e？

我认为关键是能够制造中子，我现在认为中子可能是由质子 + 电子构成的，但质量差让我感到困惑，同时物理手册将基本粒子的质量精确到小数点后第六位。

准确测量质量约为 E-27kg 的基本粒子有多容易呢？

上面的原始质子 - 质子聚变理论，包括正电子和中微子等特殊粒子，是否已被验证？

另一个可能问的问题是，如何实现呢？

那么结合能 (Eb) 到底是什么呢？我认为它是粒子的势能，但我可能错了。如果我说的没错，我们可以写成

$E_{b}(p)=V(p)=V(n)[eV]$

和

$R(p)=R(n)\approx 10^{-15}m$

R(e) 可以通过以下方式估算：

$({\frac {1}{1880}})^{1/3}\cdot R(p)\approx 10^{-16}m$

而基本粒子的密度是相同的，对于质子计算得到的值约为

${\frac {-27}{3\cdot -15}}=10^{18}kg/m^{3}$

这简直是太大了！

回到质子的结合能，我们可能会有

$V(p)={\frac {-19}{-10-15}}=1MeV=10^{-13}J$

这是从以下公式得到的：

$V={\frac {Q}{4\pi \epsilon _{0}R}}$

如果这能量等于 kT，使热电子能够穿透质子的势垒，那么我们有

$T=10^{10}K$

这也说起来很大，因为电子的尺寸大约是质子的 10 倍，所以它的势能是质子的 10 倍，现在我们有

$1+1+10+10=1+1+\Delta E_{b}$

这使得一对质子聚变可以获得 20MeV 的能量增益，一个有趣的类比是

$20MeV\cdot 10^{-19}J=20\cdot 10^{-13}Ws\approx 20\cdot 10^{-16}Wh\approx 10^{-15}Wh/particle$

现在，普通空气的体积密度在 1atm 下约为

$n_{air}\approx 10^{25}/m^{3}$

因此，如果一立方米内的所有粒子都发生聚变，我们将有 +25 次聚变，或者 +25-15=+10Wh，这转化为

$E=10^{10}Wh=10GWh$

但这是在 1atm 下...

最后，我们可以计算 +10K 时粒子的速度，大约为

$mv^{2}=10^{-13}J$

这给出

$v_{e}={\sqrt {\frac {-13}{-31}}}=9$

因此，电子穿透质子的速度必须在 1E9 m/s 的数量级上，检查质子的速度要求，我们得到

$v_{p}={\sqrt {\frac {-13}{-27}}}=7$

因此，质子要与另一个质子融合，其速度必须达到约 1E7 m/s 的数量级。

电子的速度看似不可能，因为它超过了光速，但似乎有一个被称为麦克斯韦速度分布函数的转折点，它似乎表明 kT 相对于 Ek 来说是一种平均值（我一直以为 Ek 是平均值），这意味着温度可以比 Ek 高很多， 可以这么说。

这可能是让核聚变在地球上实现的唯一希望。

在签署之前，再做一个闲聊，我相信中子的产生需要分两步进行，第一步是

$p+e+625keV=pe=H_{1}^{F}$

其中，625keV 是电子穿透质子势垒所需的估计能量，我把结果称为“融合氢”，另一步骤是

$H_{1}^{F}+780keV=n$

其中，780keV 是缺少 1,53me 以产生中子质量的爱因斯坦质量当量。

我认为这必须分步骤进行，因为我们人类无法以如此快的速度提高受控核聚变的温度，这意味着第一个过程将首先发生，然后该过程大约需要另一个 10^10K 才能完成。

因此，可能存在一种 pe 颗粒，我从未听说过，这种颗粒像中子一样带中性电荷，但质量不同，这可以通过使电子的减速超过质子穿透所需的量来解决。

我想知道中子是如何变成中子的，因为我们人类不能仅仅注入正确的质量/能量来达到中子的确切质量，它必须以某种方式“知道”它，所以我认为粒子物理学与遗传学并不遥远。

我将在此结束，继续学习大卫·K·程的《电磁场与波》，完成这本书后，我将开始认真学习弗朗西斯·F·陈的《等离子体物理学与受控核聚变》，该参考文献列在下面。

实际中的压力

标准大气压 (1atm) 是

$1atm=10^{5}Pa=10^{5}N/m^{2}=10^{4}kg/m^{2}=1kg/cm^{2}$

这只意味着我们人类已经适应了 1 kg/cm²，而没有其他适应（除了它都意味着一个实际的大气层）。

除了水深，我们还可以通过在流体中移动物体来产生压差

$p_{k}=1/2\rho v^{2}$

这个等式表明，只要有流体，我们只需移动它就能在上面产生压力。

虽然我们感受不到整整 1 kg/cm² 的压力，但我们能感受到 1 米水深产生的微小压力增加（+1hg/cm²）。

我们只需要潜入水下 10 米左右，就会因为氮气“中毒”而醉酒，这就是潜水员在这些深度用氦气而不是氧气呼吸的原因。

我们海洋最深处的压力约为 1000atm，但这只有在我们人类（需要 1atm）想要去那个地方时才能感受到（尽管如此，有些人还是去了）。船体将不得不承受相当于一头大象站在一枚一角硬币上的压力。

大气压公式

$p=p_{0}-\rho gh$

反映了不同高度的大气压 (p₀ 为 1atm)

这个公式在大约 10 公里以内是近似准确的（实际上它在那里等于 0）。

无论如何，$\rho$ 在大约 5 公里以上不再是线性的，那里

$p=p_{0}e^{-{\frac {mgh}{kT}}}$

应该被使用（m 只是分子量）。

大气层不是均匀的。有四个不同的层或球层（由温度定义）

4) 热层 (80 公里 - 卡门线)

3) 中间层 (50-80 公里)

2) 平流层 (10-50 公里)

1) 对流层 (<10 公里)

卡门线位于 100 公里处，定义为航天器需要以轨道速度飞行才能保持高度的高度。

轨道速度是指离心力等于引力的速度。

因此，大气层高达 100 公里。

数值示例

然后大气层高约 100 公里，每下降 10 米就增加 1atm 的压力，在 1000 米的深度，它加起来超过 100atm，这意味着 100kg/cm^2 或 10 吨/dm^2，这可能类似于一头大象的脚。

等离子体压力

根据理想气体定律，我们有

$p={\frac {N_{mol}}{V}}RT={\frac {N}{V}}kT=nkT$

其中，n 是（粒子）密度。

对气体做的功可以定义为 PV 乘积的增加，因为这样温度和 Ek 就会增加。

气体做的功可以定义为 PV 乘积的减少，因为这样温度就会降低。

功除以 N 得到对单个分子做的功或单个分子做的功，这反过来又得到该单个分子的温度和速度。

热力学第一定律似乎是

$dQ=dU+dW=dU+pdV=N{\frac {3}{2}}kdT+pdV$

其中，Q 表示总能量，U 表示内能，W 表示功，如果气体做功，则功为正；如果气体受到功，则功为负。

内能的定义为

$U=NEk_{p}=N{\frac {3}{2}}kT$

其中，N 表示粒子数，Ekp 表示每个粒子的动能。在封闭系统中，dQ 必须为零，因为热量既不流入也不流出。如果 dV 为正，因为气体正在做功，则内能的变化 (dU) 必须为负。

数值示例

如果在一个 1dm^3 的空气盒中，我们有 1atm 的压力，那么每立方米大约有 3E25 个粒子（这意味着盒子中有 3E22 个粒子），如果现在温度 (T) 从 300K 升高到 400K，并且我们显然有 dV=0，那么 dQ 为 62kJ，这就是需要注入的热量。

来源

1. David K. Cheng，场与波电磁学
2. Francis F. Chen，等离子体物理与受控聚变
3. Jan Petersson，数学分析，第二部分
4. http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html