实用电子学/电路分析/网格分析
外观
“网格”(也称为回路)只是一个穿过电路的路径,它从同一位置开始并结束。为了进行网格分析,网格是一个不包围其他回路的回路。
与节点分析类似,网格分析是基于KVL方程的形式化程序。需要注意的是,网格分析只能用于“平面”电路(即电路图中没有交叉但未连接的导线)。
步骤
1. 以平面形式绘制电路(如果可能)。
2. 识别网格并命名网格电流。网格电流应为顺时针方向。由两个网格共用的支路中的电流是两个网格电流的差值。
3. 针对每个网格,使用网格电流写出KVL方程。
4. 求解由此产生的方程组。
1. 依赖电压源
解决方案:相同步骤,但将依赖变量写成网格电流的函数。
2. 独立电流源
解决方案:如果电流源不在共享支路上,那么我们就得到了其中一个网格电流!如果它在共享支路上,则使用一个“超级网格”,该网格包围问题支路。为了弥补由于这样做而丢失的网格方程,使用电流源所隐含的网格电流关系(即 )。
3. 依赖电流源
解决方案:与独立电流源的步骤相同,但需要额外一步来消除依赖变量。将依赖变量写成网格电流的函数。
给定以下电路,求电流 ,.
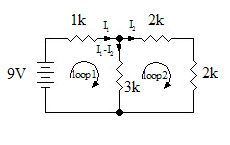
该电路有2个回路,在图中已标出。使用KVL,我们得到
回路1:
回路2:
简化后,我们得到联立方程
求解得到









