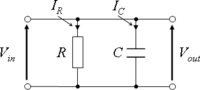
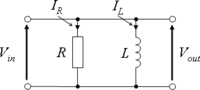
实用电子学/并联 RC

并联 RC

电路阻抗

${\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{C}}}$

${\frac {1}{Z}}={\frac {1}{R}}+j\omega C={\frac {j\omega CR+1}{R}}$

$Z=R{\frac {1}{j\omega CR+1}}$

电路响应

$I=I_{R}+I_{C}$

$I={\frac {V}{R}}+C{\frac {dV}{dt}}$

$V=(IR-RC{\frac {dV}{dt}})$

并联 RL

\

电路阻抗

${\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{L}}}$

${\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}={\frac {R+j\omega L}{j\omega RL}}$

$Z={\frac {j\omega RL}{R+j\omega L}}=j\omega L{\frac {1}{1+j\omega {\frac {L}{R}}}}$

电路响应

$I=I_{R}+I_{L}$

$I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt$

$V=IR-{\frac {R}{L}}\int Vdt$

并联 LC

电路阻抗

${\frac {1}{Z}}={\frac {1}{Z_{L}}}+{\frac {1}{Z_{C}}}$

${\frac {1}{Z}}={\frac {1}{j\omega L}}+j\omega C={\frac {(j\omega )^{2}LC+1}{j\omega L}}$

$Z={\frac {j\omega L}{(j\omega )^{2}LC+1}}$

电路响应

$I=I_{L}+I_{C}$

$I={\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}$

并联 RLC

电路阻抗

${\frac {1}{Z}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{L}}}+{\frac {1}{Z_{C}}}$

${\frac {1}{Z}}={\frac {1}{R}}+{\frac {1}{j\omega L}}+j\omega C$

${\frac {1}{Z}}={\frac {(j\omega )^{2}RLC+j\omega L+R}{j\omega RL}}$

${\frac {1}{Z}}={\frac {(j\omega )^{2}LC+j\omega {\frac {L}{R}}+1}{j\omega L}}$

电路响应

$I=I_{R}+I_{L}+I_{C}$

$I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}$

$I={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}$

$V=IR-{\frac {R}{L}}\int Vdt-CR{\frac {dV}{dt}}$

自然响应

$0={\frac {V}{R}}+{\frac {1}{L}}\int Vdt+C{\frac {dV}{dt}}$

强制响应

$I_{t}=IR+L{\frac {dI}{dt}}+{\frac {1}{C}}\int Idt$

二阶方程有两个根

ω = -α ± ${\sqrt {\alpha ^{2}-\beta ^{2}}}$

其中

$\alpha ={\frac {R}{2L}}$

$\beta ={\frac {1}{\sqrt {LC}}}$

网络的电流由下式给出

A e^{ω1 t} + B e^{ω2 t}

从上面

当${\alpha ^{2}=\beta ^{2}}$时，只有一个实根

ω = -α

当${\alpha ^{2}>\beta ^{2}}$时，有两个实根

ω = -α ± ${\sqrt {\alpha ^{2}-\beta ^{2}}}$

当${\alpha ^{2}<\beta ^{2}}$时，有两个复根

ω = -α ± j${\sqrt {\beta ^{2}-\alpha ^{2}}}$

谐振响应

在谐振时，频率相关元件的阻抗相互抵消。因此，电路的净电压为零。

$Z_{L}-Z_{C}=0$ 以及 $V_{L}+V_{C}=0$

$\omega L={\frac {1}{\omega C}}$

$\omega ={\sqrt {\frac {1}{LC}}}$

$Z=Z_{R}+(Z_{L}-Z_{C})=Z_{R}=R$

$I={\frac {V}{R}}$

在谐振频率下

$\omega ={\sqrt {\frac {1}{LC}}}$ .

$I={\frac {V}{R}}$。电流达到最大值。

进一步分析电路

当 ω = 0 时，电容器为开路。因此，I = 0。

当 ω = ∞ 时，电感器为开路。因此，I = 0。

根据三个 ω 值，即 ω = 0，${\sqrt {\frac {1}{LC}}}$，∞，我们绘制了 I 相对于 ω 的图。从图中可以看出，当电流减小到峰值电流 $I={\frac {V}{2R}}$ 的一半时，该电流值在频率带 ω₁ - ω₂ 内保持稳定，其中 ω₁ = ω_o - Δω，ω₂ = ω_o + Δω。

• 在 RLC 串联电路中，可能存在一个频率带，在这个频率带内电流保持稳定，即电流不随频率变化。为了使更宽的频率带响应，必须将电流从峰值降低。电流降低得越多，带宽就越宽。因此，该网络可以用作调谐选择带通滤波器。如果将 L 或 C 调谐到谐振频率 $\omega ={\sqrt {\frac {1}{LC}}}$。电流达到最大值 $I={\frac {V}{R}}$。然后，调整 R 的值，使它小于峰值电流 $I={\frac {V}{R}}$，通过增加 R 来获得所需的频率带。

• 如果将 R 从 R 增加到 2R，则电流现在为 $I={\frac {V}{2R}}$，它在频率带上保持稳定。

ω₁ - ω₂，其中

ω₁ = ω_o - Δω

ω₂ = ω_o + Δω

当 I 的值小于 $I={\frac {V}{2R}}$ 时，电路对宽带频率做出响应。当 I 的值介于 $I={\frac {V}{R}}$ 和 $I={\frac {V}{2R}}$ 之间时，电路对窄带频率做出响应。

摘要

电路	符号	串联	并联
RC			并联 RC 电路
阻抗	Z	$Z_{t}=R+{\frac {1}{\omega C}}={\frac {\omega CR+1}{\omega C}}$	${\frac {1}{Z_{t}}}={\frac {1}{Z_{R}}}+{\frac {1}{Z_{C}}}={\frac {1}{R}}+\omega C={\frac {R}{\omega CR+1}}$
频率	$\omega _{o}=2f_{o}$	$Z_{R}=Z_{C}$ $R={\frac {1}{\omega C}}$ $\omega ={\frac {1}{CR}}$	${\frac {1}{R}}={\frac {1}{\omega C}}$ ${\frac {1}{R}}=\omega C$ $\omega ={\frac {1}{CR}}$
电压	V	$V=IR+{\frac {1}{C}}\int Idt$	$I={\frac {V}{R}}+C{\frac {dV}{dt}}$
电流	I	$\int Idt=C(V-IR)$	${\frac {dV}{dt}}={\frac {1}{C}}(I-{\frac {V}{R}})$
相位角		Tan θ = 1/2πf RC f = 1/2π Tan CR t = 2π Tan CR	Tan θ = 1/2πf RC f = 1/2π Tan CR t = 2π Tan CR